- Записати тему та мету лабораторної роботи;
- Ознайомитись з короткими теоретичними відомостями до лабораторної роботи;
- Виконати домашнє завдання.
Проектування і особливості роботи комбінаційних цифрових пристроїв (КЦП)
Початковими даними для проектування є опис алгоритму функціонування КЦП, вимоги до основних електричних параметрів, бібліотека елементів і конструктивно-технологічні особливості побудови логічних схем.
На шляху від початкового опису алгоритму функціонування до логічної схеми КЦП можна виділити декілька основних етапів:
1. Словесний опис алгоритму функціонування КЦП;
2. Складання таблиці істинності;
3. Запис логічного виразу в ДДНФ або ДКНФ;
4. Мінімізація логічних функцій будь-яким методом;
5. Побудова схеми, яка реалізує кінцевий вираз в будь-якому базисі;
6. Перевірка працездатності спроектованої логічної схеми.
7. Проаналізувати значення функції для кожної комбінації значень аргументів.
Робота пристрою може бути задана у вигляді придатному для мінімізації (етап 2 або 3).
Для виконання синтезу ЦП в базисі І, АБО, НЕ можна використовувати як логічний вираз fМДНФ так і логічний вираз fМКНФ.
Нехай робота цифрового пристрою задана таблицею істинності
| х3х2х1 | f(x1x2x3) | ДДНФ | ДКНФ | ||
| 0 0 0 | 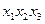
| --- | Запишемо логічну функцію: | ||
| 0 0 1 | 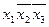
| --- | 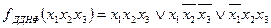
| ||
| 0 1 0 | --- | 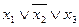
| |||
| 0 1 1 | --- | 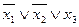
| 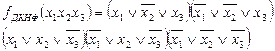
| ||
| 1 0 0 | --- | 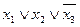
| |||
| 1 0 1 | --- | 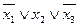
| |||
| 1 1 0 | 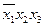
| --- | |||
| 1 1 1 | --- | 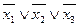
|
Як бачимо, ДДНФ більш проста, тому використовуючи карти Карно знайдемо її мінімальне значення для МДНФ:
|
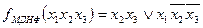
| ||||||||||||||||||
Розглянемо синтез КЦП в базисі І, АБО, НЕ використовуючи логічну функцію fМДНФ
Для побудови схеми вкажемо тип логічних елементів та їх кількість. Потрібно:
- 2 елемент «НЕ» Þ 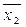 та
та 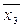
- 2 елементи «І» Þ 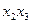 (має 2 входи) та
(має 2 входи) та 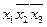 (має 3 входи)
(має 3 входи)
- 1 елемент «АБО» Þ для отримання результуючої функції fМДНФ
| Будуємо схему | Перевірка роботи схеми | |
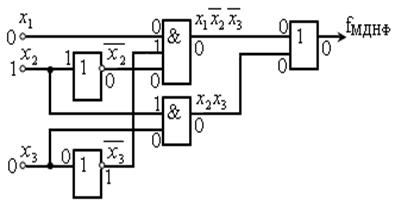
| х3 x2 x1 | 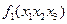
|
| 0 1 0 | ||
| 1 1 0 | ? | |
Під час розроблення складних логічних пристроїв доводиться послідовно виконувати операції типу І-НЕ, АБО-НЕ над різною кількістю змінних. Щоб перетворити логічну функцію fМДНФ або fМКНФ використовують закон подвійного заперечення та правило де Моргана, таблиця 1.
Табл. 1.
| Запис логічної функції через операцію І-НЕ | |
МДНФ
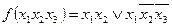
| - закон подвійного заперечення
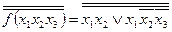 - правило де Моргана
- правило де Моргана
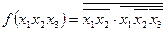
|
МКНФ
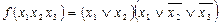
| - закон подвійного заперечення
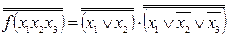 - правило де Моргана
- правило де Моргана
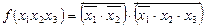 - закон подвійного заперечення
- закон подвійного заперечення
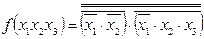
|
| Запис логічної функції через операцію АБО-НЕ | |
МДНФ
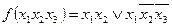
| - закон подвійного заперечення
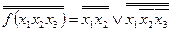 - правило де Моргана
- правило де Моргана
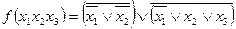 - закон подвійного заперечення
- закон подвійного заперечення
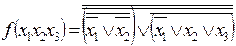
|
МКНФ
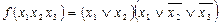
| - закон подвійного заперечення
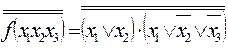 - правило де Моргана
- правило де Моргана

|





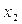

 1
1
 1
1