Выше рассмотрены простейшие модели динамики популяций с учетом конкуренции за пищевые ресурсы и влияния негативных факторов (например, эпидемий). Эти модели можно использовать для качественного анализа роста народонаселения. Конечно, рост численности населения сильно различается по разным странам и даже в развитых странах темпы роста неодинаковы. Например, в Дании, Швеции, Германии, Австрии этот показатель колеблется около нулевого значения. В таких странах, как Италия, Польша, Канада, США, рождаемость пока еще превышает смертность. Однако в целом в большинстве развитых стран ежегодный прирост населения составляет примерно 0,6% в год, тогда как в развивающихся странах – 2% в год.
В целом происходит стремительный рост населения на планете, что ставит насущную жизненную проблему управления природными ресурсами. При этом все отрасли управления ресурсами объединяет одна наука – экология и одна общая проблема – проблема оптимизации и, наконец, необходимость использовать одни и те же методы – взятие выборок, статистический анализ, математический анализ, логические процедуры, связанные с исследованием операций и анализом систем, применение вычислительной техники. Конечно, анализ и решение такой проблемы и даже какой-либо ее части представляет собой труднейшую задачу [30].
Начнем с рассмотрения простейшей задачи об оптимальном рационе, математическая модель которой допускает наглядную геометрическую интерпретацию. Пусть имеется п продуктов питания (хлеб, мясо, молоко, картофель и т.д.) и т полезных веществ (жиры, белки, углеводы и т.п.). Обозначим через aij – содержание i -го вещества в единице j- го продукта, через bi, – потребность индивидуума в i-м веществе (скажем, в месяц) и через cj, – цену единицы j -го продукта.
Обозначив потребление индивидуумом j -го продукта через хi, получаем задачу о выборе наиболее дешевого рациона питания (стоимости месячной продовольственной потребительской корзины):
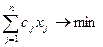(11.1)
при ограничениях
(11.2)
и
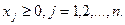(11.3)
Такая задача называется задачей линейного программирования (в стандартной форме), общая теория которой рассмотрена, например, в [2].
Прежде чем исследовать задачу (11.1)–(11.3), заметим, что ее можно представить как задачу минимизации целевой функции f(x) = 
. на множестве точек (x1,...,xn), удовлетворяющих условиям (11.2) и (11.3). Такое множество называется полиэдром и обозначается Р. Итак, мы имеем экстремальную задачу
f(х) → min, х Î Р. (11.4)
Выясним, что представляет собой данный полиэдр Р на плоскости x1Ox2 в случае двух продуктов x1 и x2. Из неравенств (11.3) вытекает, что Р расположен в первом квадранте, а каждое неравенство (11.2) геометрически определяет множество точек, лежащих по одну сторону от прямой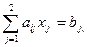 
(рис. 11.1), т. е. полиэдр Р представляет собой неограниченное множество в первом квадранте, лежащее вне области, ограниченной многоугольником OABCDEF.
Для удобства введем линии уровня целевой функции, т. е. линии, на которых в плоскости х1Oх2 целевая функция
f(х)=с1x1+с2x2 (11.5)
принимает постоянное значение, например, a, и обозначим ее Za. Очевидно, каждая линия уровня Za ={(x1,x2):f(x)=a} является прямой; при этом grad f(x)= 
является вектором N, перпендикулярным линии уровня и направленным (в данном случае) в сторону увеличения a. Таким образом, для нахождения оптимального решения нам следует перемещать линию уровня до касания с многоугольником OABCDE, при этом оптимальная прямая Z 
. коснется либо какой-то вершины (в нашем случае С), либо какого-либо ребра (например, СВ или CD при определенном изменении параметров с1 и с2).
Из приведенной геометрической интерпретации вытекает, что минимум обязательно достигается на одной из вершин многоугольника, поэтому его можно было бы найти методом перебора, сравнивая между собой значения целевой функции во всех вершинах. Конечно, метод перебора в принципе годится и в случае п переменных, однако при больших значениях п он неэффективен. Поэтому возникли и развиваются методы, позволяющие сформулировать более обозримые и эффективные критерии оптимальности. Начало им было положено работами акад. Л.В. Канторовича (1939 г.). Не углубляясь в суть этих методов, приведем пример одной многокритериальной модели.
В предыдущей задаче мы рассматривали одну целевую функцию. Однако на практике часто встречается ситуация, когда целенаправленная человеческая деятельность преследует сразу несколько целей. Такие задачи получили название многокритериальных. Методы их решения проиллюстрируем на только что рассмотренном примере составления оптимального рациона, несколько усложнив его.
Допустим, надо решить задачу об оптимальном рационе, максимизировав в нем первый продукт. Тогда наша математическая модель выглядит следующим образом:
(11.6)
Прежде чем приступить к решению, обсудим задачу, чтобы лучше понять ее специфику. Итак, забудем на время о первой целевой функции из (11.6). Тогда не составляет труда найти решение задачи:
max f 2(x)= f 2(E), xÎP (рис. 11.2). (11.7)
Однако значение первой целевой функции может быть значительно больше оптимального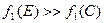 
. Совершенно аналогично обстояло бы дело, если бы мы забыли о второй целевой функции и искали минимум первой целевой функции: 
может быть много меньше f2 (Д). Приведем наиболее употребительный метод решения многокритериальных задач (в данном примере – двухкритериальной задачи), а именно сведение двух критериев к одному.
1. Для реализации этого метода необходимо «взвесить» относительную важность каждого из критериев, т. е. выбрать из внемодельных соображений число e, 0 < e < 1, а затем построить одну целевую функцию
(11.8)
Если e=1. то в расчет принимается только первая целевая функция, а если e=0, то только вторая (рис. 11.1 и 11.2). Глубокое знание реальной проблемы и накопленный опыт могут позволить выбрать 0<e<1 так, чтобы, решив оптимизационную задачу с единственной целевой функцией, можно было бы получить удовлетворительное решение для исходной постановки задачи с двумя целевыми функциями (рис. 11.3). Встретив трудности при решении двухкритериальной задачи, можно заменить ее однокритериальной, решать которую мы умеем.
Задача поиска
Более сложными, чем задачи линейного программирования, являются задачи выпуклого программирования. Прежде чем привести пример такой задачи, связанной с безопасностью жизнедеятельности, дадим некоторые определения из теории выпуклого анализа [39].
Определение 1. Множество Х из пространства Rn называется выпуклым, если из того, что две точки у и z принадлежат этому множеству, вытекает, что и весь отрезок {у,z }= {х Î Rn:х =l у +(1-l )z, 0 
l 1, соединяющий эти точки, также принадлежит этому множеству.
Очевидным примером выпуклых множеств является внутренность круга, шара, эллипсоида, куба. На рис. 11.4 а, б приведены примеры невыпуклых множеств на плоскости R2.
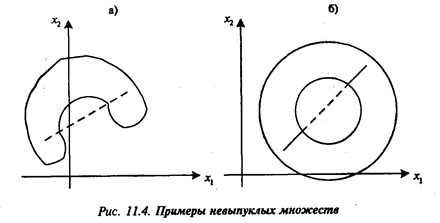
Определение 2. Функция f(x), определенная на выпуклом множестве xÌ Rn, называется выпуклой, если для любых двух точек у и z, принадлежащих X, и любого lÎx[0,1] (тогда отрезок [ly+(1-l)z], 0 l 1, целиком принадлежит X) выполняется неравенство
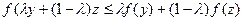, (11.9)
Замечание. Если неравенство (11.9) имеет противоположный знак, то функция f(x) называется вогнутой.
Проще всего представить график выпуклой (или вогнутой) функции на плоскости (рис. 11.5).
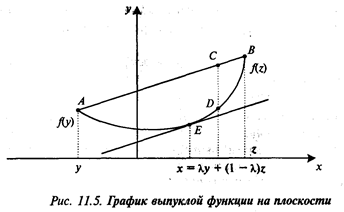
Правая часть неравенства (11.9) представляет собой отрезок АВ, соединяющий точки (y,f(y)) = А и В= (z,f(z)), причем каждая точка этого отрезка (на рисунке взята точка С) выше соответствующей точки графика (на рисунке точка D). Если функция f(x) достаточно гладкая, то условия выпуклости (вогнутости) можно выразить через ее вторую производную.
Действительно, согласно теореме Лагранжа в некоторой точке Е (рис. 11.5) касательная к графику функции АВ лежит ниже этого графика. Уравнение этой касательной Y = f(x) + f'’(x)(x-x), следовательно, f(x)- f(x) – f’(x)(x-x)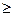 
0, откуда в силу формулы Тейлора
где 0<Q<1.
Деля последнее неравенство на (х- x)2 и далее переходя к пределу при х → x, получаем, что
f ”(x) 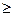0. (11.10)
В силу произвольности точки x это неравенство справедливо на всем отрезке [у, z] и является условием выпуклости (в случае вогнутости справедливо обратное неравенство). Для иллюстрации рассмотрим два простых примера.
Пример 1. f(x) =ex, xÎ (-¥,+¥), f(“) = e х > 0, следовательно, показательная функция выпукла на всей оси.
Пример 2. f(x) = sin x, xÎ[0,2p], f” (x) = - sin x, следовательно, функция sin x вогнута на отрезке [0, π] и выпукла на отрезке [π, 2 π].
Прежде чем сформулировать задачу поиска, отметим, что оптимизационная задача
f(x) → min, х Î Р (f(x) → max, х Î Р), (11.11)
где в случае max целевая функция f (х) выпукла, в случае min – вогнута и Р – полиэдр, называется задачей выпуклого программирования. Ясно, что задача линейного программирования является ее частным случаем.
Задача поиска. Объект, подлежащий обнаружению, находится в одном из п районов с вероятностями р1,..., рп соответственно. Для поиска объекта имеется общий ресурс времени Т (т. е. при t>T поиск считается нецелесообразным). Известно, что при поиске в i -м районе в течение времени ti, вероятность обнаружения объекта (при условии, что он там находится) выражается через функцию Бернулли 1- 
, где ai>0 – заданное число (формула показывает, что за бесконечное время t i объект был бы найден). Требуется распределить по районам время наблюдения (поиска) так, чтобы максимизировать вероятность обнаружения объекта. Соответствующая задача оптимизации имеет вид
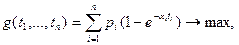(11.12)
(11.13)
(11.14)
Из теории вероятностей хорошо известно, что
(11.15)
Кроме того, очевидно, что задача g(x)→ max эквивалентна задаче (-g(x))→ min; также очевидно, что условия (11.13) и (11.14) определяют определенный полиэдр Р (рис. 11.6). Следовательно, вводя целевую функцию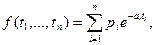 
получаем следующую оптимизационную задачу:
, (11.16)
где Р– полиэдр, заданный неравенствами (11.13) и (11.14).
Так как 
причем 
, то функция f(t) выпуклая и мы имеем задачу выпуклого программирования. Общие методы решения таких задач довольно сложны, однако в нашем конкретном случае можно предложить наглядное геометрическое решение.
Действительно, имеем 
<0. Значит, функция f(t) убывает по любому переменному ti, i = 1, 2,..., n,
и ее наименьшее значение достигается на гиперплоскости t1 + t2 +…+ tn = T(вслучае двух переменных это прямая АВ на рис. 11.6). Однако в отличие от задач линейного программирования это наименьшее значение достигается необязательно в вершинах А, В и т.д., в чем можно убедиться, исследуя на АВ функцию f(t) в случае двух переменных. Тогда f(t1,t2)=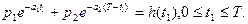 
Минимум этой функции может достигаться и внутри отрезка [0, T] в зависимости от соотношения параметров р1, р2, α1, α2, в чем можно убедиться непосредственным исследованием функции одного переменного (например, если 
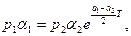то минимум достигается в середине Е отрезка АВ).
Игровые модели
Часто возникают ситуации, в которых различные участники имеют не совпадающие между собой интересы. Математические модели и методы для исследования таких так называемых конфликтных ситуаций получили название теории игр [18].
Приведем простейшие понятия и результаты этой теории. Под словом «игра» понимается совокупность правил, руководствуясь которыми игроки-участники принимают решения. Предположим, что результатом игры является плата, которую в соответствии с правилами проигравший участник платит выигравшим. Для простоты ограничимся сначала так называемыми «играми двух лиц с нулевой суммой». Для того чтобы полностью определить такую игру, нужно задать таблицу платежей – платежную матрицу, например, следующую матрицу размера 3х4:
Эта запись означает, что игрок А выбирает одну из строк этой матрицы, а игрок В, не зная выбора А, выбирает один из столбцов матрицы. Число на пересечении выбранных строки и столбца определяет выигрыш первого игрока (соответственно проигрыш второго). Например, если А выбрал вторую строку, а В – третий столбец, то А выиграл 5 единиц, а В их проиграл. Если же А выбрал третью строку, а В – второй столбец, то А проиграл 2 единицы, а В их выиграл.
Будем считать, что цель каждого из игроков состоит в максимизации наименьшего возможного выигрыша (соответственно минимизации наибольшего возможного проигрыша). Основной вопрос, возникающий в теории игр: существует ли наилучший способ игры у каждого из игроков, т. е. имеются ли у них оптимальные стратегии.
Прежде чем сформулировать ответ, вернемся к рассматриваемой матрице. Сразу видно, что игроку А выгоднее всего выбрать первую строку, так как все ее элементы больше соответствующих элементов остальных строк. Точно так же игроку В выгоднее всего выбрать второй столбец, так как все элементы этого столбца меньше соответствующих элементов остальных столбцов. Следовательно, в данном примере оптимальными стратегиями будут следующие: для А – выбор первой строки, а для В – выбор второго столбца. Число 4, стоящее на пресечении первой строки и второго столбца, носит название цены игры, т. е. платы, которую получает оптимально играющий игрок. Таким образом, в этом примере гарантированный выигрыш А – не менее 4-х единиц и гарантированный проигрыш В – не более 4-х единиц (он равен 4 единицам, если оба игрока играют оптимально).
Если оказывается, что для данной платежной матрицы минимум в какой-либо строке совпадает с максимумом в каком-либо столбце, то эти строка и столбец называются оптимальными, а их пересечение – седловой точкой платежной матрицы. Соответствующее число и будет ценой игры.
Однако далеко не каждая матрица имеет седловую точку, например, матрица 
седловой точки не имеет. Говорить здесь о максимизации наименьшего возможного выигрыша (минимизации наибольшего возможного проигрыша) возможно только при использовании так называемой смешанной стратегии при многократной игре с одной и той же платежной матрицей. Суть этой стратегии заключается в выборе разных стратегий с определенными частотами. Итак, пусть А выбирает первую строку с частотой х, а вторую – с частотой (1 – х). Аналогично для В соответствующие частоты обозначим через у и (1 –у). Тогда средний выигрыш А, обозначаемый через Е (х, у), равен
Е(х,у)=4(1-х)у+х(1-у)=х+4у-5ху. (11.17)
Нас интересует величина max min E(x,y). Имеем
x y
Еу=4-5х, (11.18)
откуда Еу>0 при 
, Ey =0 при х= 
и Еу<0 при 
. Значит,
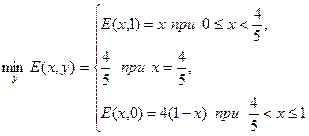
(график на рис. 11.7). Следовательно,
(11.19)
и оптимальной смешанной стратегией для А будет выбор первой строки с частотой и второй строки – с частотой 
. Средний проигрыш В, обозначаемый F(x,y), очевидно равен –Е (х, у). Нас интересует величина 
где
F(x,y)=5xy-x-4y. (11.20)
Имеем Fx=5y-1, откуда Fx< 0 при 
, Fx = 0 при y = и Fx>0 при < у ≤ 1. Значит,
(график на рис. 11.8). Следовательно,
(11.21)
и оптимальной стратегией для А будет выбор первого столбца с частотой и второго столбца – с частотой .
При оптимальных смешанных стратегиях выигрыш А и соответственно проигрыш В в пять раз меньше максимально возможного при одиночной игре.
Отметим также, что в рассмотренном примере мы показали существование оптимальных стратегий и установили равенство
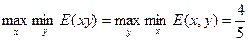; (11.22)
при этом величину Е(х,у) можно трактовать как математическое ожидание выигрыша, а величину v = определить как цену игры.
Рассмотрим теперь общий случай прямоугольной матрицы
.
При любой допустимой стратегии игрока A: x1 ≥ 0,...,хm ≥ 0, x1 +x2+…+xm=1 и любой допустимой стратегии игрока В: y1 ≥ 0,...,ym ≥ 0, y1 +y2+…+ym=1 математическое ожидание выигрыша равно
(11.23)
Множество допустимых стратегий x = (x1,…,xn) игрока А обозначим через X, а множество допустимых стратегий у=(у1,...,yn) игрока В обозначим через Y.
Рассмотренные выше примеры являются частными случаями общих теорем [18] для игр с прямоугольными матрицами (прямоугольными играми); из них, в частности, вытекает:
1. Величины 
существуют и равны между собой; при этом величина
(11.24)
является ценой игры.
2. Всякая прямоугольная игра имеет цену; каждый игрок в прямоугольной игре всегда имеет оптимальную стратегию.
3. Пусть Е – математическое ожидание выигрыша в прямоугольной игре с матрицей С, имеющей цену v. Тогда для того, чтобы элемент х* =(х1*,...,х*m)Î Х был оптимальной стратегией для игрока А, необходимо и достаточно, чтобы для всякого j =1, 2,...,n базисного вектора y(j) = 
имело место неравенство
v ≤ E (x*, y(j)). (11.25),
Аналогично для того чтобы элемент у* =(y*1,...,y*n)ÎY был оптимальной стратегией для игрока В, необходимо и достаточно, чтобы для всякого элемента базисного вектора x(i) = 
имело место неравенство
E (x(i), y*) ≤ v. (11.26)
Покажем теперь на двух примерах, как можно применить эти утверждения для вычисления цен и определения оптимальных стратегий для прямоугольных игр. В качестве таких примеров рассмотрим стратегии ловли на удочку и питания рыбы1.
1 Идея примера взята из книги Вильямса [8], которая также может служить хорошим введением в теорию игр.
Представим себе, что существование такого вида рыб, питающихся у поверхности воды, зависит от наличия трех видов летающих насекомых, которые обозначим через т1,т2 и m3 соответственно; насекомые появляются в зоне захвата с частотами 15п, 5п и п (т. е. насекомых т2 в 5 раз больше чем m3, а насекомых т1 в 3 раза больше чем т2).
Допустим, что рыбак В ловит рыбу А на насекомых одного из этих видов, насаживая их на крючок. Тогда матрица стратегий С ловли на удочку и питания рыб имеет следующий вид (табл. 11.1):
На основании изложенных утверждений достаточно найти неотрицательные числа х1,х2,х3, y1,y2,y3 и число, удовлетворяющее следующим условиям:
x1+x2+x3=l, y1+y2+y3=1, (11.27)
v ≤ -2x1, -2y1 ≤ v,
v ≤ -6x2, -6у2 ≤ v,
v ≤ -30x3, -30 у3 ≤ v.
Заменим последние шесть неравенств на равенства. Тогда имеем
х1=у1= 
, x2=y2= 
, x3=у3=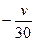 
. (11.28)
Подставляя эти значения в равенства (11.27), получим
v = 
. (11.29)
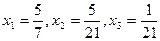. (11.30)
(11.31)
Таким образом, цена игры для рыбы будет отрицательной и равной . Она показывает, что в конце концов рыба будет поймана. При этом оптимальная стратегия рыбака совпадает со стратегией питания (также оптимальной) рыбы и оптимальная стратегия уменьшает вероятность поимки рыбы в каждом конкретном случае.
Несколько усложним задачу. Предположим, что рыболов иногда использует приманку т4, которая может быть принята по ошибке за одно из трех насекомых, но которая вдвое чаще вызывает подозрение у рыб. Тогда матрица С стратегий ловли на удочку и питания рыб примет вид табл. 11.2:
Теперь достаточно найти неотрицательные числа х1,х2,х3, y1,y2,y3,y4 и число v, удовлетворяющие следующим условиям:
x1+x2+x3=l, y1+y2+y3+y4=1, (11.27)
v ≤ -2x1, -y4 –2y1 ≤ v,
v ≤ -6x2, -3y4 – 6у2 ≤ v,
v ≤ -30x3, -15y4 – 30 у3 ≤ v.
v ≤ - x1 –3x2 –15 x3
Левая система неравенства переопределена, а правая недоопределена (в левой неизвестных больше, чем неравенств, а в правой меньше). Заметим, что если последнее неравенство в правой колонке
-15y4 – 30 у3 ≤ v. будет выполнено при у3=0, то оно будет выполнено и при всех у3>0. Следовательно, полагая у3 = 0, правую систему неравенств можно заменить системой трех линейных уравнений
-y4 –2y1 = v, -3y4 – 6у2 = v, -15y4 – 30 у3 = v
с тремя неизвестными y1, у2, у4. Ее решение, очевидно, имеет вид
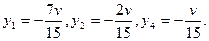
Подставляя полученные выражения в равенство (11.32), где у3 =0, получим 
, т. е. цена игры для рыбы отрицательна и равна
, (11.33)
что несколько меньше, чем в предыдущем случае. Оптимальная стратегия рыбалки имеет вид
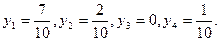(11.34)
Изучим теперь оптимальную стратегию для рыбы, так как у3, = 0, то и x3 = 0, т. е. насекомые m3 слишком опасны для жизни. Тогда из системы четырех неравенств выпадают третье и четвертое, которое при x3 = 0 является следствием двух первых (их полусуммой). Таким образом, для определения x1, х2 и v имеем систему трех уравнений с тремя неизвестными
x1 + x2 + x3 = 1, v = -2x1, v = -6x2,
откуда
и, с учетом x3 = 0,
(11.35)
Значит, оптимальная стратегия для рыбы равна
(11.36)
цена же ее в силу (11.35) равна 
, т. е. совпадает с (11.34), что, вообще говоря, вытекает из общей теории.
Модели, основанные на теории игр, представляют собой интересный, но пока еще недостаточно изученный подход к решению стратегических экологических задач. Разработка теории для более сложных игр с ненулевой суммой и игр многих лиц, где между игроками могут создаваться коалиции, должна найти эффективное применение в экологических проектах, связанных с планированием и оценкой различных воздействий на окружающую среду.
Контрольные задания
1. Рассмотрим задачу об «оптимальном рационе» в случае трех продуктов питания (например, хлебные, молочные и мясные продукты) и трех полезных веществ (углеводы, белки, жиры). Ценовой вектор с = (с1, с2, c3) (руб.) примерно равен (10; 20; 50), а вектор b = (b1, b2, b3) минимально необходимого месячного потребления полезных веществ (кг) равен (1,2; 4; 1,5). Будем предполагать также, что матрица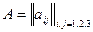 
имеет вид 
.
Решить задачу f1(x)= 
→ min при ограничениях Ах ≤ b, х ≥ 0.
2. При тех же ограничениях решить задачу f2(x) = х2 → max.
3. Решить двухкритериальную задачу f1(x)→ min, f2(x)→ max, заменяя ее минимизацией суперкритерия f(x)= Θ f1(x)-(1- Θ )f2(x). Рассмотреть случаи 
.
4. Привести геометрическую интерпретацию задач 1–3.
5. Рассмотреть задачу поиска в случае трех районов и соотношения 
= 1: 2: 3. Найти условия на параметры p1, р2, p3, при которых задача имеет решение в каждом из районов, т.е. t1 = Т, t2=Т, t3 = Т, и в случае, когда время поиска в каждом из районов одно и то же (t1 = t2 = t3 = T/3).
6. Найти оптимальную стратегию рыбака, использующего в качестве наживки мух и живца, если матрица стратегий имеет вид:
7. Найти оптимальную стратегию рыбака, если он дополнительно использует искусственных мух и блесну, а матрица стратегий в этом случае имеет вид:
