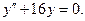| Основні типи диференціальних рівнянь, що інтегруються у квадратурах | ||
| Назва | Вид | Загальний розв’язок (загальний інтеграл) диференціального рівняння або рекомендації щодо його розв’язання |
| Диференціальне рівняння з відокремленими змінними | 
| 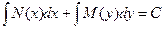
|
| Диференціальне рівняння з відокремлюваними змінними | 
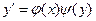
| 
 
|
| Однорідне диференціальне рівняння першого порядку | 
| Заміною  , , 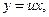 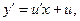 де де  рівняння зводиться до рівняння з відокремлюваними змінними рівняння зводиться до рівняння з відокремлюваними змінними
|
| Лінійне рівняння | 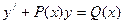
| Заміна:  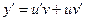 , де u=u(x),v=v(x) , де u=u(x),v=v(x)
|
| Рівняння Бернуллі | 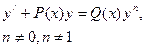
| Заміна:  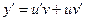 ,
де u=u(x),v=v(x) ,
де u=u(x),v=v(x)
|
| Диференціальні рівняння другого порядку, які допускають зниження порядку | ||
| Вид рівняння | Заміна | Розв’язання |

| 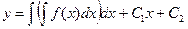
| |
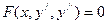 - явно не містить шуканої функції y - явно не містить шуканої функції y
|  , де z(x) – нова невідома функція змінної x , де z(x) – нова невідома функція змінної x
|
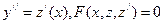
|
 - явно не містить незалежної змінної х - явно не містить незалежної змінної х
|  , де z(у) – нова невідома функція змінної у , де z(у) – нова невідома функція змінної у
| 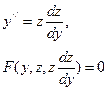
|
| Лінійні однорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами | ||
| Вид рівняння | Характеристичне рівняння | Загальний розв’язок |


| 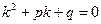
| 1. 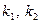 – дійсні різні: – дійсні різні:
 ;
2. ;
2. 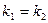 – дійсні і рівні: – дійсні і рівні:
 3.
3. 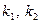 - комплексно-спряжені,
тобто - комплексно-спряжені,
тобто 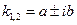 : :
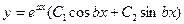
|
| Неоднорідні диференціальні рівняння другого порядку зі сталими коефіцієнтами, що мають спеціальну праву частину | ||
| Вид диференціаль-ного рівняння | Структура загального розв’язку | Структура частинного розв’язку неоднорідного рівняння |

| 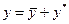 ,
де ,
де 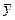 – загальний розв’язок однорідного диференціального – загальний розв’язок однорідного диференціального
| а) якщо  , то , то 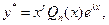 де r - кратність кореня де r - кратність кореня 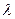 характеристичного рівняння ( характеристичного рівняння (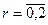 ), ),  -многочлен степеня n з буквенними коефіцієнтами; -многочлен степеня n з буквенними коефіцієнтами;
|
рівняння
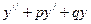 = 0; = 0;  – частинний розв’язок неоднорідного рівняння – частинний розв’язок неоднорідного рівняння
| б) якщо 
 то то  , де , де 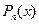 , ,  - многочлени степеня - многочлени степеня  з буквенними коефіцієнтами, r – кратність кореня з буквенними коефіцієнтами, r – кратність кореня 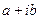 характеристичного рівняння характеристичного рівняння
|
Запитання для самоконтролю
1. Що називається звичайним диференціальним рівнянням? його порядком? загальним розв’язком? частинним розв’язком?
2. Сформулюйте теорему Коші існування і єдиності розв’язку диференціального рівняння першого порядку.
3. Які види диференціальних рівнянь І-го порядку Ви знаєте і як вони інтегруються?
4. Дайте означення диференціального рівняння вищого порядку, його загального та частинного розв’язку.
5. Нагадайте типи диференціальних рівнянь другого порядку, що допускають зниження порядку. Як вони інтегруються?
6. Дайте означення лінійного однорідного диференціального рівняння другого порядку із сталими коефіцієнтами. Який вигляд мають частинні розв’язки даних рівнянь в залежності від коренів характеристичного рівняння?
7. Як знайти загальні розв’язки лінійних неоднорідних диференціальних рівнянь другого порядку із сталими коефіцієнтами і спеціальною правою частиною?
8. У чому полягає метод виключення розв’язання системи диференціальних рівнянь першого порядку?
Рекомендована література: [1], розділ 5; [8], розділ XIII, §1-8, §16-17, §20-25, §29; [5], ч.3, практичні заняття 17-21.
Приклад 6. Проінтегрувати диференціальні рівняння:
а)  б)
б) 
в)  г)
г) 
д) 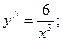 е)
е) 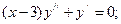 є)
є) 
ж) 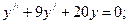 з)
з) 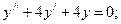
и) 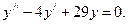
Розв’язання. а) Маємо диференціальне рівняння першого порядку з відокремлюваними змінними. Перепишемо його у вигляді
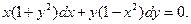
Відокремлюючи у ньому змінні і інтегруючи, будемо мати:


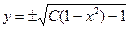 – загальний розв’язок диференціального рівняння.
– загальний розв’язок диференціального рівняння.
б) Це також диференціальне рівняння першого порядку з відокремлюваними змінними. Запишемо його у вигляді
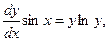 звідки
звідки 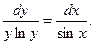 Інтегруємо ліву і праву частини рівняння. Одержимо:
Інтегруємо ліву і праву частини рівняння. Одержимо:

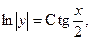
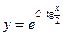 – загальний розв’язок диференціального рівняння.
– загальний розв’язок диференціального рівняння.
Використовуючи початкову умову  , знайдемо значення сталої С і частинний розв’язок даного рівняння:
, знайдемо значення сталої С і частинний розв’язок даного рівняння: 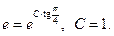
Підставляючи С= 1 у знайдений загальний розв’язок, одержимо частинний розв’язок рівняння 
Зауважимо, що дане рівняння має також тривіальні розв’язки:
у = 0 і ln y = 0, y = 1. Розв’язок у = 1 входить у загальний розв’язок за умови, що С = 0.
в) Маємо однорідне диференціальне рівняння першого порядку. Запишемо його у вигляді  Покладаючи
Покладаючи  де u=u(x), отримаємо рівняння з відокремлюваними змінними:
де u=u(x), отримаємо рівняння з відокремлюваними змінними:
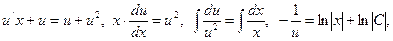
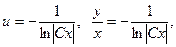
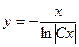 - загальний розв’язок диференціального рівняння.
- загальний розв’язок диференціального рівняння.
г) Дане рівняння є лінійним диференціальним рівнянням першого порядку. Робимо підстановку: y=u×v, y/ = u/ v + u v/, де u = u(x), v = v(x).
Отримаємо рівняння
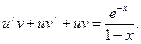 Звідки
Звідки 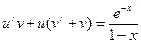 (1)
(1)
Одну із функцій u або v ми можемо вибрати довільно. Виберемо функцію v так, щоб в рівності (1) вираз у дужках дорівнював нулеві. Розв’яжемо два рівняння: 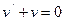 і
і 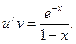
У першому рівнянні відокремимо змінні і, проінтегрувавши його, знайдемо v:

Надамо сталій інтегрування довільного, зручного для обчислень значення. Нехай С 1 = 0, тоді: 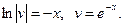
З другого рівняння знайдемо и:


Загальний розв’язок вихідного рівняння запишеться: 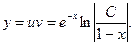
Знайдемо С, використавши початкову умову: 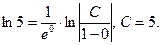 Тоді шуканий частинний розв’язок
Тоді шуканий частинний розв’язок
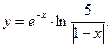
д) У заданому рівнянні можливе зниження порядку. Будемо двічі інтегрувати його праву частину:
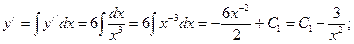
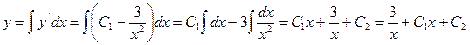 – шуканий загальний розв’язок диференціального рівняння.
– шуканий загальний розв’язок диференціального рівняння.
е) Маємо диференціальне рівняння другого порядку, що не містить у явному вигляді змінну у. Знижуємо порядок рівняння за допомогою введення нової функції: 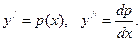 Одержимо:
Одержимо:

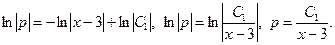
Підставивши в останню рівність  отримаємо:
отримаємо:
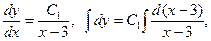
 – загальний розв’язок диференціального рівняння.
– загальний розв’язок диференціального рівняння.
є) Це диференціальне рівняння другого порядку, що не містить у явному вигляді змінну х. Знижуємо порядок рівняння за допомогою введення нової функції: 
Одержимо: 
Якщо  то
то 
Оскільки  то
то 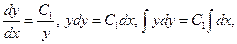
 – шуканий загальний інтеграл диференціального рівняння.
– шуканий загальний інтеграл диференціального рівняння.
Зауважимо, що розв’язок р= 0 можна одержати із загального при С1 = 0 і тому, він не є особливим.
ж) Маємо лінійне однорідне диференціальне рівняння другого порядку із сталими коефіцієнтами (ЛОДР). Складемо його характеристичне рівняння: 
За теоремою Вієта знаходимо корені характеристичного рівняння:
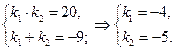
Оскільки корені характеристичного рівняння – дійсні і різні (k1≠k2), то задане ДР має два частинні розв’язки:  та
та 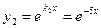 . Ці розв’язки лінійно незалежні
. Ці розв’язки лінійно незалежні  , то загальний розв’язок вихідного ДР запишеться
, то загальний розв’язок вихідного ДР запишеться  де С 1, С 2 – довільні сталі.
де С 1, С 2 – довільні сталі.
Зауважимо, що корені рівняння k2 + p k + q = 0 зручно шукати за формулою 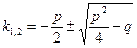 (*).
(*).
з) Задане рівняння також є ЛОДР із сталими коефіцієнтами. Його характеристичне рівняння k 2 + 4 k + 4 = 0. Корені характеристич-ного рівняння знайдемо за формулою (*): 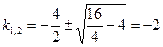 .
.
Отже, k1=k2= -2.
Оскільки корені характеристичного рівняння – дійсні і рівні між собою (k1=k2= k), то частинні розв’язки ДР запишуться: y 1 =e- 2 x,
y 2 =x e- 2 x 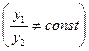 .
.
Шуканий загальний розв’язок ДР:
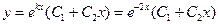 , де С 1, С 2 – довільні сталі.
, де С 1, С 2 – довільні сталі.
и) Запишемо характеристичне рівняння заданого ЛОДР і знайдемо його корені: k2 - 4 k + 29 = 0, 
Характеристичне рівняння має спряжені комплексні корені k 1,2 =a±bi, причому a=2, b=5. Частинні розв’язки ДР:

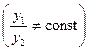 .
.
Шуканий загальний розв’язок вихідного ДР:
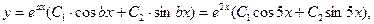 де С 1, С 2 – довільні сталі.
де С 1, С 2 – довільні сталі.
Завдання для самоконтролю
Проінтегрувати диференціальні рівняння:
1. 

 2.
2. 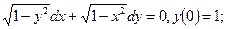
3. 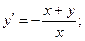 4.
4. 
 5.
5. 
6. 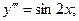 7.
7.  8.
8.  9.
9. 
10. 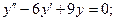 11.
11.