| Назва поняття, позначення | Означення | Аналітичний запис |
Похідна
функції
y=f(x) в точці x (похідна першого порядку); 
| Похідною функції y=f(x) в точці x називається границя відношення приросту функції  в цій точці до приросту аргументу в цій точці до приросту аргументу  , коли приріст аргументу прямує до нуля. , коли приріст аргументу прямує до нуля.
| 
|
Правила диференціювання
Нехай u(x) та v(x) – деякі диференційовні функції, с - стала, тоді:
1.  ; 5.
; 5. 
2.  ; 6.
; 6. 
3.  7.
7. 
4.  8.
8. 
Правило диференціювання складеної функції.
Якщо y=f(u) і u=u(x), тобто y=f(u(x)), де функції f і u – мають похідні, то  .
.
| Таблиця похідних | |
| елементарних функцій | складеної диференційовної функції u=u(x) |
1. 
| 
|
2. 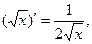  ; ;
|   ; ;
|
3. 
| 
|
4.  
|  
|
5. 
| 
|
6.   ; ;
|   ; ;
|
7.   ; ;
|   ; ;
|
8. 
| 
|
9. 
| 
|
10. 
| 
|
11. 
| 
|
12.   ; ;
|   ; ;
|
13.   ; ;
|   ; ;
|
14. 
| 
|
15. 
| 
|
| Таблиця диференціалів Нехай u=u(x) – диференційовна функція, тоді: | |
1. 
| 9. 
|
2. 
| 10. 
|
3. 
| 11. 
|
4. 
| 12. 
|
5. 
| 13. 
|
6. 
| 14. 
|
7. 
| 15. 
|
8. 
|
Зауваження. Кожна з формул, наведених у таблиці, справедлива на проміжку, що належить області визначення відповідної функції.
Запитання для самоконтролю
1. Дайте означення похідної функції. Який її геометричний і механічний зміст?
2. Які основні правила диференціювання?
3. Запишіть таблицю похідних основних елементарних функцій.
4. Яка функція називається складеною і як вона диференціюється?
5. Як знайти похідні обернених, параметрично і наявно заданих функцій?
6. У чому полягає метод логарифмічного диференціювання?
7. Що називається диференціалом функції? Який його геометричний зміст? Запишіть формулу застосування диференціала
до наближених обчислень.
8.Що називається похідною n-го порядку функції?
9.Згадайте загальну схему дослідження функції і побудови її графіка.
10. Як знайти найбільше та найменше значення функції на відрізку?
Рекомендована література: [1], розділ 3; [8], розділ III, розділ IV, розділ V §1-11; [5], ч. 2, практичні заняття 21-36.
Приклад 3.1. Користуючись правилами диференціювання, знайти похідні  заданих функцій:
заданих функцій:
а)  б)
б) 
в)  г)
г) 
д)  е)
е) 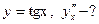
Розв’язання. Дана функція є складеною відносно змінної х. Позначимо  тоді
тоді  Застосувавши правило диференціювання складеної функції
Застосувавши правило диференціювання складеної функції  , будемо мати:
, будемо мати:
 б) Функція представлена у вигляді суми двох функцій, причому перший доданок – складена функція, а другий – добуток двох функцій. Використовуючи відповідні правила диференціювання, будемо мати:
б) Функція представлена у вигляді суми двох функцій, причому перший доданок – складена функція, а другий – добуток двох функцій. Використовуючи відповідні правила диференціювання, будемо мати:


в) Використавши властивості логарифмів, перепишемо функцію у вигляді 
 Тоді
Тоді
 г) Маємо показниково-степеневу функцію. Застосуємо метод логарифмічного диференціювання. Отримаємо:
г) Маємо показниково-степеневу функцію. Застосуємо метод логарифмічного диференціювання. Отримаємо:





д) Похідну  параметрично заданої функції визначимо за формулою
параметрично заданої функції визначимо за формулою 
Знаходимо 
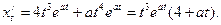
Тоді 
е) Знаходимо послідовно першу і другу похідні даної функції:

Приклад 3.2. Обчислити наближено 
Розв’язання. Для знаходження наближеного значення функції,
використаємо формулу  В нашому випадку
В нашому випадку  – значення функції f(x) =
– значення функції f(x) =  при x= =
при x= =  =0,98. Покладемо x 0 = 1 (значення, близьке до 0,98, при
=0,98. Покладемо x 0 = 1 (значення, близьке до 0,98, при
якому  легко обчислюється без таблиці:
легко обчислюється без таблиці:  =
=
 ). Тоді
). Тоді 
Оскільки  то
то 
Отже, 
Приклад 3.3. Знайти рівняння дотичної і нормалі до кривої  в точці
в точці 
Розв’язання. Рівняння дотичної і нормалі до графіка функції  в точці
в точці  відповідно мають вигляд:
відповідно мають вигляд:
 і
і  .
.
Знайдемо похідну заданої функції і її значення в точці  :
:

 Тоді
Тоді  або
або  - рівняння дотичної, а
- рівняння дотичної, а 
 – рівняння нормалі.
– рівняння нормалі.

Приклад 3.4. Знайти найбільший об’єм циліндра, вписаного в заданий конус.
Розв’язання. 1) Визначаємо, які величини фіксовані (відомі з умови задачі), а які змінні.
Оскільки задано конус, то АО=R і ОС=Н – фіксовані величини.
В конус можна вписати багато циліндрів, змінюючи його висоту ОО 1 і радіус О 1 Д 1. Тому ОО 1 =х і О 1 Д 1 =у – змінні величини (невідомі).
2) Вибираємо незалежну змінну.
Нехай висота циліндра ОО 1 =х – незалежна змінна – аргумент, причому х є [0; Н ].
3) За умовою задачі визначаємо функцію двох змінних z = f(x;y).
У нашому випадку об’єм циліндра V=V(x;y)=πxy2 – шукана функція.
4) Виражаємо одну змінну через іншу.
Для нашого випадку виразимо змінну у через змінну х.
З подібності трикутників ВОС і Д 1 О 1 С випливає, що 

Тоді  - досліджувана функція.
- досліджувана функція.
5) Знаходимо критичні точки знайденої функції.


Оскільки при 
 , а при
, а при 
 то в точці
то в точці  - функція має максимум.
- функція має максимум.
Отже, максимальний об’єм циліндра 
Приклад 3.5. Подати число 66 у вигляді суми двох доданків так, щоб добуток цих чисел був найбільшим.
Розв’язання. Нехай одне із задуманих чисел х, а друге – у. За умовою задачі х+у= 66, звідки у= 66 -х. Добуток чисел Р=ху=х (66-- x) = 66 х-х2 – досліджувана функція. Знаходимо 
 при х= 33. Ця точка буде критичною. Оскільки
при х= 33. Ця точка буде критичною. Оскільки  , то в точці х= 33 досліджувана функція має максимум. При цьому у= 66-33=33.
, то в точці х= 33 досліджувана функція має максимум. При цьому у= 66-33=33.
Отже, добуток чисел буде найбільшим, якщо х=у= 33.
Завдання для самоконтролю
1. Користуючись правилами диференціювання, знайти похідні  заданих функцій:
заданих функцій:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  д)
д) 
2. Обчислити наближено
а)  ; б)
; б)  .
.
3. Знайти рівняння дотичної і нормалі до кривої  в точці М 0(2;2).
в точці М 0(2;2).
4. Визначити найменшу площу рівнобедреного трикутника, описаного навколо кола радіуса r.
Невизначений інтеграл
| Назва поняття, означення | Аналітичний запис |
Функція F(x) називається первісною функції f(x) на проміжку (a;b), якщо F(x) диференційовна на (a;b) і справджується рівність  =f(x), =f(x), 
|  =f(x) для =f(x) для 
|
Невизначеним інтегралом
функції f(x) називається сукупність усіх первісних F(x)+C заданої функції.
Позначення: 
|  , де , де
 – знак інтеграла;
f(x)dx – підінтегральний вираз;
f(x) – підінтегральна функція;
x – змінна інтегрування;
C=const (довільна стала) – знак інтеграла;
f(x)dx – підінтегральний вираз;
f(x) – підінтегральна функція;
x – змінна інтегрування;
C=const (довільна стала)
|
| Основні властивості невизначеного інтеграла (правила інтегрування) | |
| Властивості (правила) | Аналітичний запис |
| Похідна від невизначеного інтеграла дорівнює підінтегральній функції. | 
|
| Диференціал від невизначеного інтеграла дорівнює підінтеграль-ному виразу. | 
|
| Невизначений інтеграл від диферен-ціала деякої функції дорівнює сумі цієї функції і довільної сталої. | 
|
| Сталий множник можна винести за знак інтеграла. |  де k=const
де k=const
|
| Невизначений інтеграл від алгебраїчної суми функцій f(x) та g(x) дорівнює алгебраїчній сумі невизначених інтегралів від цих функцій за умови, що f(x) та g(x) мають первісні. | 
|
| Таблиця основних невизначених інтегралів Нехай u=u(x) – диференційовна функція, тоді: | |
1. 

| 12. 
|
2. 
| 13. 
|
3. 
| 14. 
|
4. 
| 15. 
|
5. 
| 16. 
|
6. 
| 17. 
|
7. 
| 18. 
|
8. 
| 19. 
|
9. 
| 20. 
|
10. 
| 21. 
|
11. 
| 22.  . .
|
Зауваження. Кожна з формул, наведених у таблиці, справедлива на проміжку, що належить області визначення підінтегральної функції.
| Основні методи інтегрування | |
| Назва | Суть |
| Метод безпосереднього інтегрування | Базується на основних властивостях невизначеного інтеграла, таблиці інтегралів, а також використанні операції підведення під знак диференціала.
Метод підведення під знак диференціала дає можливість звести нетабличний інтеграл відносно змінної х до табличного інтеграла відносно змінної u(x).
При цьому використовуються таблиця диферен-ціалів і такі правила:
1)  2)
2) 
|
| Метод заміни змінної |  (f(x) має первісну на інтервалі (a;b); φ(х) визначена і диференційовна на інтервалі (α;β), причому φ(α)=а; φ(β)=b)
(f(x) має первісну на інтервалі (a;b); φ(х) визначена і диференційовна на інтервалі (α;β), причому φ(α)=а; φ(β)=b)
|
| Метод інтегрування частинами |  (функції u=u(x) і v=v(x) мають на деякому проміжку неперервні похідні).
Рекомендації до застосування методу:
1. Якщо
(функції u=u(x) і v=v(x) мають на деякому проміжку неперервні похідні).
Рекомендації до застосування методу:
1. Якщо  то то  . .
|
2. Якщо  то то  ,
де ,
де  – многочлен степеня n.
3. Якщо – многочлен степеня n.
3. Якщо  то можливий довільний вибір співмножників u і dv. то можливий довільний вибір співмножників u і dv.
| |
Інтегрування
виразів, що
містять
квадратний
тричлен
 
|       
|
| Інтегрування раціональних дробів | |||
| Раціональні дроби | Інтеграли від раціональних дробів | ||
Найпростіші раціональні дроби
Типу І: 
|

| ||
Типу ІІ:  , де , де   Типу ІІІ:
Типу ІІІ:  , де , де

|


| ||
Правильний раціональний дріб
 , де , де 
| Інтеграл  зводиться до інтегрування
суми найпростіших дробів типів І-ІІІ.
При цьому слід пам’ятати:
1. Дійсному простому кореню знаменника х=а відповідає дріб типу І: зводиться до інтегрування
суми найпростіших дробів типів І-ІІІ.
При цьому слід пам’ятати:
1. Дійсному простому кореню знаменника х=а відповідає дріб типу І:  .
2. Дійсному кореню знаменника x=b кратності l відповідає сума l дробів типів І і ІІ: .
2. Дійсному кореню знаменника x=b кратності l відповідає сума l дробів типів І і ІІ:

| ||
3. Парі комплексно-спряжених коренів знаменника або квадратному тричлену x2+px+q з  відповідає дріб типу: відповідає дріб типу: 
| ||
Неправильний раціональний дріб
 , де , де 
|  , де Tm-n(x) – многочлен (ціла частина дробу); , де Tm-n(x) – многочлен (ціла частина дробу);
 – правильний раціональний дріб (p<n) – правильний раціональний дріб (p<n)
| |
| Інтегрування найпростіших ірраціональних функцій | |
Інтеграл
 – раціональна функція вказаних аргументів; – раціональна функція вказаних аргументів;
| Підстановка |

|  , де k – спільний знаменник дробів , де k – спільний знаменник дробів 
|

|  , де k – спільний знаменник дробів , де k – спільний знаменник дробів 
|

|  , де k – спільний знаменник дробів , де k – спільний знаменник дробів 
|

| x = a tg t (або x = a сtg t) |

| x =  (або x = (або x =  ) )
|

| x =a sin t ( або x = a cos t) |
| Інтегрування найпростіших тригонометричних функцій | |
| Інтеграл | Підстановка або формули для перетворення виразів перед інтегруванням |

| Універсальна тригонометрична підстановка

|
 ,
де p і q – цілі числа ,
де p і q – цілі числа
| 
|

| 
|

| 
|

| 
|
 , де m, n – цілі числа , де m, n – цілі числа
| Зводиться до інтеграла від раціональної функції або до табличного:
а) якщо m – парне, а n – непарне, то використовують підстановку  б) якщо m – непарне, а n – парне, то використовують підстановку
б) якщо m – непарне, а n – парне, то використовують підстановку  в) якщо m,n – парні і невід’ємні, то використовують формули зниження степеня:
в) якщо m,n – парні і невід’ємні, то використовують формули зниження степеня:
|

 ;
г) якщо m,n – парні, але принаймі одне з них від’ємне, то використовують підстановку ;
г) якщо m,n – парні, але принаймі одне з них від’ємне, то використовують підстановку  (або (або  ) )
| |

| 
|

| 
|

| 
|
Запитання для самоконтролю
1. Яка функція називається первісною для заданої функції?
2. Що називається невизначеним інтегралом? Який його геометричний зміст?
3. Які властивості невизначеного інтеграла Ви знаєте?
4. Запишіть таблицю основних інтегралів та диференціалів.
5. Охарактеризуйте основні методи інтегрування: метод підведення під знак диференціала, метод заміни змінної, інтегрування частинами. Наведіть приклади.
6. Як інтегруються раціональні дроби, ірраціональні і тригонометричні вирази? Згадайте необхідні теореми і формули. Наведіть приклади.
Рекомендована література: [1], розділ 4, п.4.1; [8], розділ X; [5], ч.3, практичні заняття 1-9.
Приклад 4.1. Знайти невизначені інтеграли:
а)  б)
б)  в)
в)  г)
г) 
д)  е)
е)  є)
є)  ж)
ж) 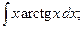
з) 
 ; ї)
; ї)  й)
й)  к)
к)  л)
л)  м)
м)  н)
н)  о)
о)  п)
п) 
Розв’язання. Поділимо почленно чисельник підінтегрального дробу на його знаменник і, застосувавши властивості невизначеного інтеграла, будемо мати:

У прикладах б) – г) застосуємо метод підведення під знак диференціала.
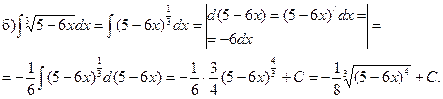



Для знаходження інтегралів д) – ж) використаємо метод інтегру-вання частинами.




 з) Маємо інтеграл від виразу, що містить квадратний тричлен.
з) Маємо інтеграл від виразу, що містить квадратний тричлен.
Виділимо в чисельнику підінтегральної функції доданок, що рівний похідній знаменника. Тоді 
 і) Підінтегральна функція є правильним раціональним дробом. Розкладемо знаменник дробу на прості множники, а дріб на суму найпростіших раціональних дробів. Маємо:
і) Підінтегральна функція є правильним раціональним дробом. Розкладемо знаменник дробу на прості множники, а дріб на суму найпростіших раціональних дробів. Маємо:
 Зведемо праву частину останньої рівності до спільного знаменника і, прирівнявши чисельники дробів, отримаємо тотожність:
Зведемо праву частину останньої рівності до спільного знаменника і, прирівнявши чисельники дробів, отримаємо тотожність:

Невідомі коефіцієнти визначимо методом колокації (надамо змінній x значень, що відповідають дійсним кореням знаменника дробу, і підставимо їх в останню рівність):


 Звідки А=- 1, В= 6, С= -2.
Звідки А=- 1, В= 6, С= -2.
Знайдені коефіцієнти підставимо в розклад підінтегральної функції на найпростіші дроби. Одержимо:

ї) Підінтегральна функція є неправильним раціональним дробом. Представимо його у вигляді суми цілої частини (многочлена) і правильного раціонального дробу. Для цього виконаємо ділення чисельника дробу на знаменник:




Знаменник правильного раціонального дробу розкладемо на прості множники, а дріб на суму найпростіших раціональних дробів і складемо тотожність.

 .
.
Коефіцієнти  і
і  шукаємо за методом невизначених коефіцієнтів. Для цього прирівняємо коефіцієнти при однакових степенях
шукаємо за методом невизначених коефіцієнтів. Для цього прирівняємо коефіцієнти при однакових степенях  лівої і правої частини тотожності:
лівої і правої частини тотожності:


 Звідки А= 0, В= 1, С= -1, D =-1.
Звідки А= 0, В= 1, С= -1, D =-1.
Отже, 
У прикладах й) – л) маємо інтеграли від ірраціональних функцій. Обчислимо їх за допомогою відповідних підстановок, які зведуть вихідний інтеграл до інтеграла від раціональної функції.



 У прикладах м) – п) маємо інтеграли від виразів, що містять тригонометричні функції.
У прикладах м) – п) маємо інтеграли від виразів, що містять тригонометричні функції.
м) Використаємо універсальну тригонометричну підстановку.

н) Використаємо формулу зниження степеня. 



Завдання для самоконтролю
Знайти невизначені інтеграли:
1. 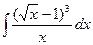 ; 2.
; 2.  ; 3.
; 3.  ; 4.
; 4.  ;
;
5.  ; 6.
; 6.  ; 7.
; 7.  ;
;
8.  ; 9.
; 9.  ; 10.
; 10.  ;
;
11.  ;12.
;12.  ; 13.
; 13.  ; 14.
; 14.  ;
;
15.  ; 16.
; 16.  .
.
Визначений інтеграл
| Обчислення визначеного інтеграла | |
| Назва | Аналітичний запис |
| Формула Ньютона-Лейбніца |  , де – F(x) первісна функції f(x) на [ a;b ], , де – F(x) первісна функції f(x) на [ a;b ],  - знак подвійної підстановки - знак подвійної підстановки
|
| Формула заміни змінної у визначеному інтегралі | 
|
| Формула визначеного інтегрування частинами | 
|
| Застосування визначеного інтеграла (геометричні задачі) | |||
| Назва поняття | Геометричне зображення | Формули для обчислення | |
Площа плоскої фігури:
а) площа криволінійної трапеції, якщо 
| 
| а) криву задано явно:
 б) криву задано параметрично:
б) криву задано параметрично:
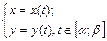

| |
б) площа криволінійної трапеції, якщо 
| 
| 
| |
| в) площа фігури, зображеної на рисунку | 
| 
| |
| г) площа фігури, обмеженої кривими y=f1(x), y=f2(x) та прямими x=a, x=b | 
| 

| |
| Довжина дуги кривої |

| а) криву задано явно:

 б) криву задано параметрично:
б) криву задано параметрично:
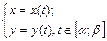

| |
| Об’єм тіла обертання |
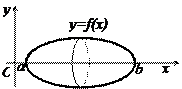
| 
| |
Запитання для самоконтролю
1. Дайте означення визначеного інтеграла. Які його властивості?
2. Запишіть формулу Ньютона-Лейбніца.
3. Які основні методи обчислення визначених інтегралів Ви знаєте?
4. Дайте означення невласних інтегралів І-го і ІІ-го роду. Як вони обчислюються?
5. Наведіть приклади задач з геометрії і фізики, що розв’язуються за допомогою визначеного інтеграла. Запишіть необхідні формули.
Рекомендована література: [1], розділ 4, п.4.2; [8], розділ XI, §1-7, розділ XII, §1-7; [5], ч.3, практичні заняття 10-13, 15-16.
Приклад 5.1. Знайти інтеграли:
а)  б)
б)  в)
в) 
Розв’язання. а) Використаємо метод підведення під знак диференціала.

б) Застосуємо формулу визначеного інтегрування частинами:

Тоді

в) Обчислимо інтеграл, використавши метод заміни змінної.

 Приклад 5.2. Обчислити невласні інтеграли або довести їх розбіжність:
Приклад 5.2. Обчислити невласні інтеграли або довести їх розбіжність:
а)  б)
б) 
Розв’язання. а) Маємо невласний інтеграл першого роду.

Інтеграл збігається.
б) Маємо невласний інтеграл другого роду.
Підінтегральна функція терпить нескінчений розрив при х = 0.

Інтеграл розбігається.
 Приклад 5.3. Обчислити площу фігури, обмеженої лініями
Приклад 5.3. Обчислити площу фігури, обмеженої лініями
у = 3 х – х2, у = -х.
 Розв’язання. Знайдемо точки перетину прямої у =f 1(x) = -х і параболи у = f 2(x) = 3 х-
Розв’язання. Знайдемо точки перетину прямої у =f 1(x) = -х і параболи у = f 2(x) = 3 х-  .
.
Точки перетину ліній О (0;0) і А (4;-4).
Площа цієї фігури:

Завдання для самоконтролю
1. Знайти інтеграли:
а)  ; б)
; б)  ; в)
; в) 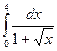 .
.
2. Обчислити невласні інтеграли або довести їх розбіжність:
а)  ; б)
; б)  .
.
3. Обчислити площу фігури, обмеженої лініями:
а)  ; б)
; б)  .
.






