1. Какое уравнение называется
а) общим уравнением плоскости;
б) уравнением плоскости в отрезках?
2. Какие уравнения называются параметрическими уравнениями плоскости?
3. Каков геометрический смысл коэффициентов каждого из перечисленных в пунктах 1-2 уравнений прямой?
4. Какое уравнение называется
а) векторным уравнением плоскости;
б) векторно-параметрическим уравнением плоскости?
5. Любую ли плоскость можно задать
а) общим уравнением;
б) уравнением в отрезках;
в) параметрическими уравнениями?;
6. Сколько существует для заданной плоскости
а) общих уравнений;
б) уравнений в отрезках;
в) параметрических уравнений?
7. Пусть плоскость задана одним из уравнений, перечисленных в пунктах 1-2. Как перейти для этой плоскости к другим из этих уравнений?
8. Как установить, лежит ли заданная точка М 0(х0;y0;z0) на заданной плоскости (рассмотрите различные способы задания плоскости)?
9. Найдите угол между плоскостями:
а) A 1 x + B 1 y + C 1 Z+D 1=0 и A 2x+ B 2y+ C 2 Z+D 2=0;
б) Ax + By + C Z+D =0 и x = x 0+ lu+  , y = y 0+ mu+
, y = y 0+ mu+  ; z=z0+nu+
; z=z0+nu+ 
в)  и x = x 0+ lu+
и x = x 0+ lu+  , y = y 0+ mu+
, y = y 0+ mu+  , z=z0+nu+
, z=z0+nu+  .
.
10. Запишите условия
а) совпадения двух плоскостей;
б) параллельности двух плоскостей;
в) пересечения двух плоскостей;
г) перпендикулярности двух плоскостей.
(Рассмотрите различные сочетания способов задания двух плоскостей).
11. Как вычислить расстояние от точки М 0(х0;y0;z0) до заданной плоскости (рассмотрите различные способы задания плоскости с помощью уравнений из пунктов 1–2)?
12. Какому условию должны удовлетворять коэффициенты уравнения плоскости, которая
а) параллельна координатной плоскости 0xz
б) параллельна оси ординат;
в) проходит через начало координат?
13. Пусть плоскость задается уравнением Ax + By + Cz+D =0. Запишите условие принадлежности двух точек М 1(х1;y1;z1), М 2(х2;y2;z2) одному полупространству, определяемому этой плоскостью.
| Примеры: |
1. Запишите общее уравнение плоскости, содержащей точки М 1(1;2;3), М 2(0;4;1), М 3(3;1;1)
Р е ш е н и е: Векторы  ,
, 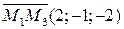 являются направляющими для данной плоскости. Значит, точка М(х;у;z) принадлежит искомой плоскости тогда и только тогда, когда векторы
являются направляющими для данной плоскости. Значит, точка М(х;у;z) принадлежит искомой плоскости тогда и только тогда, когда векторы  ,
,  ,
, 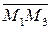 компланарны, что эквивалентно тому, что
компланарны, что эквивалентно тому, что
их смешанное произведение равно нулю, т. е. 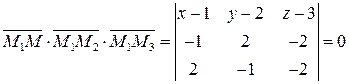 . Отсюда получаем
. Отсюда получаем  или
или  (рис.3).
(рис.3).
О т в е т: 
2. Запишите параметрические уравнения плоскости, содержащей точки 

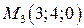 .
.
Р е ш е н и е: При таком способе задания плоскости сразу записывается ответ в виде параметрических уравнений: берем в качестве начальной точки этой плоскости, например, точку  , в качестве направляющих векторов, например, векторы
, в качестве направляющих векторов, например, векторы  и
и  Тогда получим (рис.3).
Тогда получим (рис.3).
О т в е т:  .
.
3. Запишите уравнение плоскости, которая проходит через точку М 0(1;–2;3) и отсекает на координатных осях отрезки одинаковой величины.
Р е ш е н и е: Уравнение искомой плоскости удобно здесь находить в виде уравнения в отрезках:  . Исходя из геометрического смысла коэффициентов этого уравнения и условия задачи, имеем, что a = b = c. Учитывая, что точка М 0 лежит на этой плоскости, находим а:
. Исходя из геометрического смысла коэффициентов этого уравнения и условия задачи, имеем, что a = b = c. Учитывая, что точка М 0 лежит на этой плоскости, находим а: 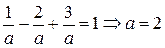 . Таким образом, получим
. Таким образом, получим
О т в е т: 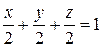 .
.
4. Запишите общее уравнение плоскости  ,
,  ,
,  .
.
 Р е ш е н и е:: Из геометрического смысла коэффициентов параметри ческих уравнений плоскости получаем, что точка М0(1;2;1) принадлежит этой плоскости, а векторы
Р е ш е н и е:: Из геометрического смысла коэффициентов параметри ческих уравнений плоскости получаем, что точка М0(1;2;1) принадлежит этой плоскости, а векторы  ,
, 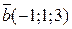 параллельны ей. Но тогда вектор
параллельны ей. Но тогда вектор
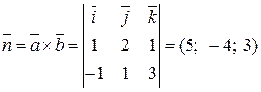
будет ортогонален этой плоскости. Поэтому общее уравнение этой плоскости можно задать в виде:
 . Подставляя в это уравнение координаты точки
. Подставляя в это уравнение координаты точки  , вычислим
, вычислим  :
:
 . Отсюда
. Отсюда  . Следовательно,
. Следовательно,
О т в е т:  (рис.4).
(рис.4).
5. Выясните, которая из координатных плоскостей принадлежит пучку, определяемому плоскостями  и
и 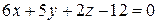 .
.
Р е ш е н и е: Как известно, уравнение любой плоскости этого пучка может быть записано в виде:  или
или  (**),
(**),
где  и
и  одновременно не равны нулю.
одновременно не равны нулю.
Так как любая из координатных плоскостей проходит через начало координат, то должно быть, что  . Отсюда
. Отсюда  , но тогда из уравнения (**) получаем
, но тогда из уравнения (**) получаем 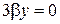 или
или  , так как
, так как  .
.
О т в е т:  .
.
6. Напишите уравнения плоскостей, делящих пополам двугранные углы между плоскостями  и
и  .
.
Р е ш е н и е: Искомые плоскости – множество точек, равноудаленных от заданных плоскостей.
Пусть  - точка этих искомых плоскостей.
- точка этих искомых плоскостей.
Тогда 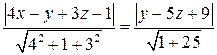 , что эквивалентно
, что эквивалентно
 . Раскрывая модуль, получим два линейных уравнения: 1)
. Раскрывая модуль, получим два линейных уравнения: 1) 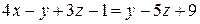 или
или 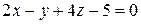 ; 2)
; 2)  или
или  . Эти уравнения и задают искомые плоскости.
. Эти уравнения и задают искомые плоскости.
О т в е т: 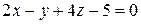 и
и  .
.
 по теме “ПЛОСКОСТЬ ”
по теме “ПЛОСКОСТЬ ”
1. Дана плоскость  .
.
1) Укажите какой-либо нормальный вектор этой плоскости.
2) Укажите какой-либо направляющий вектор этой плоскости.
3) Принадлежит ли точка 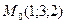 заданной плоскости?
заданной плоскости?
4) Найдите величины отрезков, отсекаемых этой плоскостью на координатных осях.
5) Выпишите какие-либо параметрические уравнения заданной плоскости.
6) Вычислите расстояние от точки М(2;0;1) до заданной плоскости.
7) Лежат ли точки 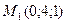 и
и  в одном полупространстве, определяемом заданной плоскостью?
в одном полупространстве, определяемом заданной плоскостью?
8) Вычислите косинус угла между заданной плоскостью и плоскостью
x+3y+2z-7=0.
2. Вычислите значение параметра D, при котором плоскость
x- 3y+4z+D=0 проходит через точку М(4;1;0).
3. Вычислите значение параметров А и С, при которых плоскости x+5y-7z+1=0 и Аx-10y+Cz-7=0 параллельны
4. Запишите множество, задающее все плоскости, параллельные вектору  .
.
5. Дана плоскость x=2-u+3v, y=u+v, z=3-u.
1) Укажите два какие-либо неколлинеарные направляющие векторы этой плоскости.
2) Укажите какой-либо нормальный вектор этой плоскости.
3) Установите, лежит ли на этой плоскости точка М(4;2;2).
4) Запишите какое-либо общее уравнение этой плоскости.
5) Запишите какие-либо параметрические уравнения плоскости, проходящей через точку  параллельно заданной плоскости.
параллельно заданной плоскости.
6) Запишите для заданной плоскости уравнение в отрезках.
7) Вычислите расстояние от точки  до заданной плоскости.
до заданной плоскости.
8) Вычислите косинус угла между заданной плоскостью и плоскостью
4x+y+3z-1=0.
6. Запишите какие-либо параметрические уравнения плоскости, проходящей через точку  параллельно векторам
параллельно векторам 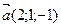 и
и  .
.

ПРЯМАЯ
В ПРОСТРАНСТВЕ






