Уравнения длинной линии синусоидального тока в комплексной форме

79 Вторичные параметры (коэффициент распространения и волновое сопротивление). При распространении электромагнитной энергии по длинной кабельной линии напряжение между проводниками и ток в проводниках не остаются постоянными, а меняются по абсолютному значению и по фазе. Отношения между током и напряжением в любой точке цепи и током и напряжением в начале цепи зависят от двух параметров – волнового сопротивления Z_в и коэффициента распространения γ, которые носят название вторичных параметров передачи. Они относятся к основным показателям, характеризующим электрические свойства цепи.

Волновое сопротивление определяется отношением напряжения к току в любой точке цепи и выражается через первичные параметры по формуле

__________________

Z_в = √ (R + iωL) / (G + iωC).

Волновое сопротивление выражается в Омах, если активное сопротивление R выражено в Ом/км, индуктивность L – в Г/км, емкость С – в Ф/км и проводимость G – в См/км. В общем виде волновое сопротивление является комплексной величиной. Для всех однородных цепей R/L > G/C, поэтому угол волнового сопротивления отрицателен. При R << ωL и G << ωL, т.е. для частот свыше 5…10 кГц, волновое сопротивление определяется по следующей упрощенной формуле ____

Z_в = √ L / C)

Коэффициент распространения γ характеризует изменение мощности электромагнитной волны при распространении ее по линии и изменение фазы напряжения и тока вдоль линии. Коэффициент распространения – комплексная величина, причем действительная составляющая α определяет затухание, т.е. уменьшение напряжения и тока на единицу длины цепи, а мнимая составляющая β характеризует величину изменения фазы напряжения и тока на единицу длины линии. Коэффициент распространения через первичные параметры выражается формулой _________________

γ = α + iβ = √ (R + iωL) · (G + iωC)

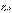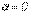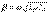80 Уравнение длинны линии в гиперболически функциях. Линией без потерь называется линия, у которой первичные параметры и равны нулю. В этом случае, как было показано ранее, и . Таким образом,

,

откуда . Раскроем гиперболические функции от комплексного аргумента :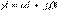

Тогда для линии без потерь, т.е. при , имеют место соотношения:

и .

Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента: ;

.

81 Длинная лилия как четырехполюсник напряжения и токи в начале и в конце линии связаны между собой соотношениями

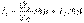Эти уравнения соответствуют уравнениям симметричного четырехполюсника, коэффициенты которого ; 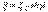и ; при этом условие выполняется. Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий

 

82 Волны в линии Длинная линия — регулярная линия передачи, длина которой превышает длину волны (λ) колебаний, распространяющихся в линии. Характерной особенностью длинных линий является проявление интерференции двух волн, распространяющихся навстречу друг другу. Одна из этих волн создается генератором электромагнитных колебаний, подключенным к линии, и называется падающей. Другая волна может возникать из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии, и называется отраженной. Отраженная волна распространяется в направлении, обратном падающей волне. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами. Различают три режима работы линии:

1. режим бегущей волны; ^[

2. режим стоячей волны; ^[10]

3. режим смешанных волн.

Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме B _U = 0, | Г | = 0, k _бв = k _св = 1^[10].

Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей B _U = A _U т.е. энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, k _св = , k _бв = 0^[10].

В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 < B _U < A _U т.е. часть мощности падающей волны теряется в нагрузке, а остальная часть в виде отраженной волны возвращается обратно в генератор. При этом 0 < | Г | < 1, 1 < k _св < , 0 < k _бв < 1

 

83 Фазовая скорость. Длина волны. Фазовая скорость определяется из условия, что , откуда следует, что .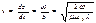

Длина волны l равна расстоянию, на котором фаза волны изменяется на 2p, т. е. , откуда . На расстоянии длины волны z =l зату­хание волны составит раз.

 

 

84 Неискажающая линия. Пусть сигнал, который требуется передать без искажений по линии, является периодическим, т.е. его можно разложить в ряд Фурье. Сигнал будет искажаться, если для составляющих его гармонических затухание и фазовая скорость различны, т.е. если последние являются функциями частоты. Таким образом, для отсутствия искажений, что очень важно, например, в линиях передачи информации, необходимо, чтобы все гармоники распространялись с одинаковой скоростью и одинаковым затуханием, поскольку только в этом случае, сложившись, они образуют в конце линии сигнал, подобный входному.

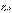Идеальным в этом случае является так называемая линия без потерь, у которой сопротивление и проводимость равны нулю.

Действительно, в этом случае

,

т.е. независимо от частоты коэффициент затухания и фазовая скорость

.

Однако искажения могут отсутствовать и в линии с потерями. для получения и , что обеспечивает отсутствие искажений, необходимо, чтобы , т.е. чтобы волновое сопротивление не зависело от частоты. , при (4)

есть вещественная константа.

Линия, параметры которой удовлетворяют условию (4), называется линией без искажений.

85 Длинная линия без потерь. В линии без потерь погонные параметры R ₁ = 0 и G ₁ = 0. Поэтому для коэффициента распространения γ и волнового сопротивления W получим:

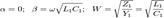
С учетом этого выражения для напряжения и тока примут вид: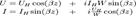

 

86 Стоячие воины в длинной линии без потерь. Бегущая волна отсутствует (т.е. волна стоит). Перемещения энергии нет. Перемещение энергии будет отсутствовать в следующих случаях: - при холостом ходе - при КЗ

- при чисто реактивной нагрузке.

Рассмотрим режим холостого хода:

 

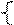
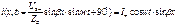
где - амплитуда синусоиды.

Точки, в которых напряжение и ток все время остаются равными 0, называются узлами. Точки, в которых напряжение и ток достигают максимальных значений, называются пучностями. На любом расстоянии от конца линии U и I сдвинуты на 90⁰.

87. Переходные процессы в длинных линиях без потерь. В цепях с сосредоточенными параметрами переходные процессы проте­кают одно­временно во всех направлениях цепи с одинаковой скоростью затуха­ния.

В цепях с распределенными параметрами переходной процесс, начав­шийся в какой-либо точке цепи, распространяется на остальные элементы в виде волн, которые распро­страняются вдоль цепи с конечной скоростью v. Эта скорость близка к скорости света 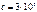км/c в воздушных линиях и v < c для кабельных линий. По мере распространения вдоль линии волна изменяет свою форму, поэтому переходной процесс в разных точках ли­нии выглядит по-раз­ному. Таким образом, переходной процесс в цепи с распределенными парамет­рами протекает в функции двух переменных – пространства и время. В высоковольтных линиях электропередачи переходные процессы возни­кают при раз­личных коммутациях, а так же от грозовых явлений в атмосфере. При переходом процессе на отдельных участках линии могут возникнуть пере­напряжения, нередко приводящие к пробою изоляции, или большие токи, вызы­вающие механические разрушения конструкций

 

88. Расчет падающих и отраженных волн при расчете переходных процессов. Пусть линия с волновым сопротивлением в момент t = 0 под­ключается к источнику ЭДС 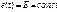или с нулевыми или с ненулевыми внутренними параметрами .

1 Источник постоянной ЭДС e(t) = E с нулевыми внутренними парамет­рами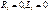

После замыкания рубильника в момент t =0 возникнут падающие волны с прямоуголь­ным фронтом: 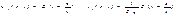Во всех точках линии, пройденных фронтом волны, устанавливается постоян­ный режим (), u (t) =E, . Для точек линии, куда фронт не дошел (), u =0 и i =0

2, Источник синусоидальной ЭДС с нулевыми внут­ренними па­раметрами

Напряжение и ток в начале линии после замыкания рубильника устано­вятся мгно­венно и будут равны:

, .

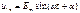Таким образом, для расчета падающих волн в линии , необходимо выполнить расчет переходного процесса в схеме замещения для начала линии и в получен­ных выражениях заменить переменную t на .

После того как падающие волны 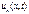и 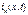достигнут конца линии, при возникнут отраженные волны и законы распределения напряжения и тока вдоль линии будут определяться наложением этих волн: