Характер свободной составляющей в цепи 2-го порядка.
Характер свободной составляющей в цепи второго порядка.
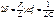
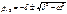
1) 
; 
- функция имеет апериодический характер.
2) 
;
,
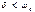где 
- корни комплексно сопряженные.
Свободная составляющая будет носить колебательный характер.
3) Дискриминант равен нулю и корни будут действительные равные (предельный случай апериодического режима).
47. Последовательность расчета переходных процессов классическим методом. 1) Записываем искомое решение в виде установившейся и свободной составляющей. Для цепи первого порядка решение имеет вид:
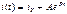
2) Находим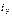 
(установившуюся составляющую) для послекоммутационной схемы.
3) Найдем корень характеристического уравнения. Составляем характеристическое уравнение для послекоммутационной схемы, и, решая его, находим корни характеристического уравнения. Характеристическое уравнение может быть получено двумя способами:
а) Из комплексного входного сопротивления, записанного для послекоммутационной схемы, где “ 
”заменяется на “ 
”, причем входное сопротивление приравнивается к нулю
б) Из дифференциального уравнения, составленного по законам Кирхгофа для послекоммутационной схемы.
Поскольку входное сопротивление записывается для свободной составляющей, то можно считать, что источник находится в ветви с любым реактивным элементом и удобнее записывать комплексные входные сопротивления для этого случая. 4) Определяем i в момент времени t=0 (зависимые и независимые начальные условия, и, если необходимо, их производные).
5) Определяем постоянные интегрирования:
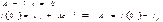
6) Подставляем все величины, найденные в пп. 2 – 6 в исходное уравнение.
Основные понятия операторного метода расчета переходных процессов..
Функция 
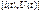называется оригиналом.
Функция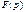 
называется изображением. Метод расчета, основанный на замене оригиналов их изображениями, называется операторным. Это позволяет перейти от дифференциальных уравнений к алгебраическим. Переход от оригиналов к изображениям осуществляется с помощью прямого преобразования Лапласа:
, где 
- комплексный оператор.
Переход от изображений к оригиналам осуществляется с помощью обратного преобразования Лапласа:
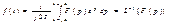
Найдем изображения некоторых простейших функций
1) 
, тогда:
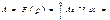
2) 
, тогда:
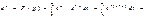
3) 
тогда:
4) Пусть 
. Тогда:
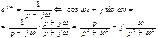
Основные законы и формулы операторного метода, расчет переходных процессов.
1) Сумме оригиналов соответствует сумма изображений.
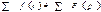
2) Умножению оригинала на постоянное число соответствует умножение изображения на то же число:
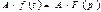
3) Дифференцированию оригинала соответствует умножение изображения на “p” – значение функции в момент времени “t=0”.
4) Интегрированию оригинала соответствует деление изображения на оператор “p”:
Найдем напряжение на индуктивности:
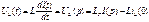
Найдем ток и напряжение в емкости:
Напряжение на емкости:
- напряжение на емкости при нулевых начальных условиях.
При ненулевых начальных условиях:
50 Основные законы электрических цепей в операторной форме записи. 
Перейдем от оригиналов к изображениям:
Изображение тока равно:
(1)
Здесь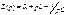 
- операторное сопротивление цепи. Оно может быть получено из комплексного сопротивления путем замены “jω” на “p”. Это соответствует переходу от преобразования Фурье к преобразованию Лапласа:
- закон Ома при нулевых начальных условиях. Уравнению (1) соответствует следующая схема замещения:
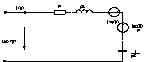В этой операторной схеме замещения ненулевые начальные условия учитываются введением дополнительных внутренних источников ЭДС, причем источник 
направлен по направлению протекающего тока, а источник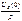 
, учитывающий напряжение на емкости, направляется навстречу протекающему току. Первый закон Кирхгофа в операторной форме выглядит следующим образом: 
Второй закон Кирхгофа в операторной форме:
Для расчета операторных схем замещения применяются все известные методы, основанные на законах Кирхгофа.
51. Переход от изображений к оригиналам. Формула разложения. Переход от изображений к оригиналам осуществляется двумя способами:
