Cеминар: Применение производной при исследовании функции
Основные вопросы
1. Признаки монотонности функции.
2.Необходимое условие существования экстремума.
3. Критические точки на экстремум.
4. Достаточные условия существования экстремума.
5. Наибольшее и наименьшее значение функции на отрезке.
6. Выпуклость и вогнутость графика функции.
7. Точки, критические на перегиб.
8. Необходимое и достаточное условия существования перегиба.
9. Асимптоты графика функции.
Задания для семинара
№1 Доказать монотонность функции на всей числовой оси:
а)  , б)
, б)  ,
,
в)  , г)
, г)  .
.
№2 При каких а функции монотонны всюду:
а)  , б)
, б)  .
.
№3 Найти интервалы монотонности и экстремумы функций:
а)  , б)
, б)  ,
,
в)  , г)
, г)  .
.
№4 С помощью 2-го достаточного условия существования экстремума исследовать поведение функции в указанной
точке х о:
а)  ,
,
б)  ,
,
в)  ,
,
г)  .
.
№5 Найти экстремумы, точки перегиба. Построить график.
а)  , б)
, б)  .
.
№6 Определить выпуклость или вогнутость графика функции
в окрестности указанных точек:
а)  ,
,
б)  .
.
№7 Найти асимптоты и построить график: а) 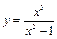 ,
,
б)  .
.
№8 Найти наибольшее и наименьшее значение функции на заданном отрезке:
а)  , б)
, б)  .
.
Задания для самостоятельной работы
№9 Доказать монотонность функции на всей числовой оси:
а)  , б)
, б)  , в)
, в)  .
.
№10 При каких а функции монотонны всюду:
а)  , б)
, б)  .
.
№11 Найти интервалы монотонности и экстремумы функций:
а)  , б)
, б)  ,
,
в)  .
.
№12 С помощью 2-го достаточного условия существования экстремума исследовать поведение функции в указанной
точке х о:
а)  ,
,
б)  ,
,
в)  ,
,
г)  .
.
№ 13 Найти экстремумы, точки перегиба. Построить график.
а)  , б)
, б) 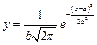 .
.
№ 14 Определить выпуклость или вогнутость графика функции
в окрестности указанных точек:
а)  ,
,
б)  .
.
№ 15 Найти асимптоты и построить график:
а)  , б)
, б) 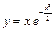 .
.
№16 Найти наибольшее и наименьшее значение функции на заданном отрезке: а)  , б)
, б) 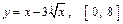 .
.
Ответы
2. а)  ; б) при
; б) при  , при
, при 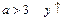 .
.
3. а) при  , при
, при  ,
,
 ;
;
б)  ;
;
в) 
 ;
;
г)  )
) 
4. а)  , б)
, б)  , в) нет экстремума, г) х о не является критической точкой.
, в) нет экстремума, г) х о не является критической точкой.
5. а)  ,
,
 ; б)
; б)  ,
,  ,
,  .
.
6. а)  - выпуклый график,
- выпуклый график,  -вогнутый; б)
-вогнутый; б)  - выпуклый график,
- выпуклый график,
 -вогнутый. 7. а)
-вогнутый. 7. а) 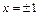 - вертикальные асимптоты,
- вертикальные асимптоты,  наклонная асимптота,
наклонная асимптота, 
 ; б)
; б)  горизонтальная асимптота, в)
горизонтальная асимптота, в) 
 .
.
8. а)  ; б)
; б)  .
.
10. a)  , в)
, в)  .
.
11. а)  ,
, 
 б)
б) 
 , в)
, в)  .
.
12. а)  , б)
, б)  , в) нет экстремума, г) х о не является критической точкой.
, в) нет экстремума, г) х о не является критической точкой.
13. а) нет точек экстремума, 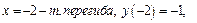
б) 
14. а)  - выпуклый график,
- выпуклый график,  -вогнутый; б)
-вогнутый; б)  - вогнутый график,
- вогнутый график,
 - выпуклый.
- выпуклый.
15. а)  горизонтальные асимптоты,
горизонтальные асимптоты, 
 ;
;
б)  .
.
16. а)  , б)
, б) 
Семинар: Неопределенный интеграл
Вопросы к семинару:
1. Первообразная и неопределенный интеграл.
2.Таблица интегралов. Вычисление неопределенных интегралов с помощью таблицы интегралов.
3. Нахождение интегралов методом компенсирующего множителя или введением под знак дифференциала.
4. Нахождение интегралов с помощью замены.
5. Метод интегрирования по частям.
Таблица простых интегралов
(х – независимая переменная) 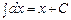









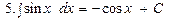

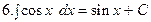



Таблица интегралов сложных функций 









Формула интегрирования по частям 
таблица выбора функции U(x)

| |

| |

|
Правила применения таблицы:
1. Если подынтегральное выражение является произведением функций из разных строк таблицы, то за U принимается функция, стоящая в таблице выше. Оставшееся выражение принимается за dV. При этом, выбирая U, следует всегда заботиться о том, чтобы dV было легко интегрируемым.
2. Если же подынтегральное выражение будет произведением функций из одной строки, то за U можно принять любую из этих функций. При этом интегрирование по частям, как правило, применяют дважды и получают равенство - уравнение, в котором неизвестным является искомый интеграл.
Задания для семинара
№1 Вычислить с помощью таблицы интегралов
а)  , б)
, б)  ,
,
в)  , г)
, г)  .
.
№2 Найти интегралы методом компенсирующего множителя или введением под знак дифференциала
а)  , б)
, б)  , в)
, в)  , г)
, г)  ,
,
д)  ,
,
е)  ,
,
ж)  ,
,
з)  ,
,
и)  .
.
№3 (Устно) Найти интегралы
а)  , б)
, б)  , в)
, в)  , г)
, г)  ,
,
д)  ,
,
е)  ,
,
ж)  , з)
, з)  .
.
№4 Найти интегралы с помощью замены переменной:
а)  , б)
, б)  , в)
, в)  , г)
, г)  .
.
№5 Найти интегралы методом интегрирования по частям:
а)  , б)
, б)  , в)
, в)  , г)
, г) 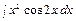 . д)
. д)  е)
е)  , ж)
, ж) 






