§ 4.1. Индивидуальное домашнее задание (ИДЗ) по теме: “Предел функции и непрерывность”
Задача 1. Найти пределы:
1.1. 
| 1.2. 
|
1.3. 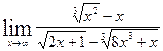
| 1.4. 
|
1.5. 
| 1.6. 
|
1.7. 
| 1.8. 
|
1.9. 
| 1.10 
|
1.11 
| 1.12. 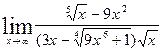
|
1.13. 
| 1.14. 
|
1.15. 
| 1.16. 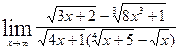
|
1.17. 
| 1.18. 
|
1.19. 
| 1.20. 
|
1.21. 
| 1.22. 
|
1.23. 
| 1.24. 
|
1.25. 
| 1.26. 
|
1.27. 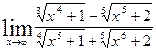
| 1.28. 
|
1.29. 
| 1.30. 
|
Задача 2. Найти пределы.
2.1. 
| 2.2. 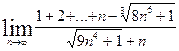
| |||
2.3. 
| 2.4. 
| |||
2.5. 
| 2.6. 
| |||
2.7. 
| 2.8. 
| |||
2.9. 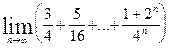
| 2.10. 
| |||
2.11. 
| ||||
2.13. 
| ||||
2.14. 
| ||||
2.15. 
| ||||
2.16. 
| ||||
2.17. 
| ||||
2.18. 
| ||||
2.19. 
| ||||
2.20.  2.21.
2.21. 
| ||||
2.22. 
| ||||
2.23. 
| ||||
2.25. 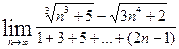
| ||||
2.26.  2.27.
2.27. 
| ||||
2.28. 
| ||||
2.29. 
| ||||
2.30. 
| ||||
Задача 3. Доказать непрерывность функции f (x) в точке x 0.
| 3.1. f(x)=6-x2, x0=2 | 3.2. f(x)=3x2-2, x0=-2 |
| 3.3. f(x)=-2x2-3, x0=3 | 3.4. f(x)=2x2+5, x0=-3 |
| 3.5. f(x)=5x2-1, x0=4 | 3.6. f(x)=2-3x2, x0=4 |
| 3.7. f(x)=4x2-3, x0=-1 | 3.8. f(x)=4x2+5, x0=2 |
| 3.9. f(x)=x2+7, x0=-3 | 3.10. f(x)=7-2x2, x0=3 |
| 3.11. f(x)=-2x2-7, x0=2 | 3.12. f(x)=3x2+2, x0=4 |
| 3.13. f (x)= 5x2+3, x0=-2 | 3.14. f(x)=4x2-1, x0=-3 |
| 3.15. f(x)=7x2-1, x0=4 | 3.16. f(x)=-8x2-1, x0=1 |
| 3.17. f(x)=2x2+11, x0=5 | 3.18. f(x)=10x2-3, x0=5 |
| 3.19. f(x)=13-2x2, x0=3 | 3.20. f(x)=3-10x2, x0=4 |
| 3.21. f(x)=4x2-11, x0=-2 | 3.22. f(x)=1-5x2, x0=2 |
| 3.23. f(x)=3-4x2, x0=1 | 3.24. f(x)=-7-x2, x0=1 |
| 3.25. f(x)=x2-6, x0=3 | 3.26. f(x)=9-5x2, x0=-2 |
| 3.27. f(x)=7-5x2, x0=-2 | 3.28. f(x)=-2x2-1, x0=3 |
| 3.29. f(x)=11-3x2, x0=2 | 3.30. f(x)=4x2-15, x0=-1 |
Задача 4. Найти пределы разложением на множители и по правилу Лопиталя.
4.1. 
| 4.2. 
|
4.3. 
| 4.4. 
|
4.5. 
| 4.6. 
|
4.7. 
| 4.8. 
|
4.9. 
| 4.10. 
|
4.11. 
| 4.12. 
|
4.13. 
| 4.14. 
|
4.15. 
| 4.16. 
|
4.17. 
| 4.18. 
|
4.19. 
| 4.20. 
|
4.21. 
| 4.22. 
|
4.23. 
| 4.24. 
|
4.25. 
| 4.26. 
|
4.27. 
| 4.28. 
|
4.29. 
| 4.30. 
|
Задача 5. Найти пределы, используя метод освобождения от иррациональности.
5.1. 
| 5.2. 
| |
5.3. 
| 5.4. 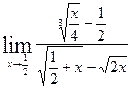
| |
5.5. 
| 5.6. 
| |
5.7. 
| 5.8. 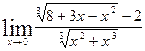
| |
5.9. 
| 5.10. 
| |
5.11. 
| 5.12. 
| |
5.13. 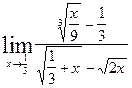
| 5.14. 
| |
5.15. 
| 5.16. 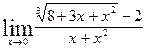
| |
5.17. 
| 5.18. 
| |
5.19. 
| 5.20. 
| |
5.21. 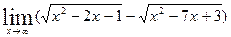
| ||
5.22. 
| 5.23. 
| |
5.24. 
| 5.25. 
| |
5.26. 
| 5.27. 
| |
5.28. 
| 5.29. 
| |
5.30. 
| ||
Задача 6. Найти пределы, используя эквивалентные бесконечно-малые.
6.1. 
| 6.2. 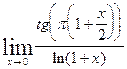
|
6.3. 
| 6.4. 
|
6.5. 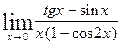
| 6.6. 
|
6.7. 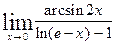
| 6.8. 
|
6.9. 
| 6.10. 
|
6.11. 
| 6.12. 
|
6.13. 
| 6.14. 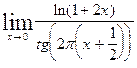
|
6.15. 
| 6.16. 
|
6.17. 
| 6.18. 
|
6.19. 
| 6.20. 
|
6.21. 
| 6.22. 
|
6.23. 
| 6.24. 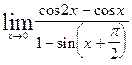
|
6.25. 
| 6.26. 
|
6.27. 
| 6.28. 
|
6.29. 
| 6.30. 
|
Задача 7. Найти пределы, используя эквивалентные бесконечно малые.
7.1. 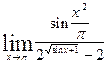
| 7.2. 
|
7.3. 
| 7.4. 
|
7.5. 
| 7.6. 
|
7.7. 
| 7.8. 
|
7.9. 
| 7.10. 
|
7.11. 
| 7.12. 
|
7.13. 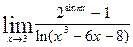
| 7.14. 
|
7.15. 
| 7.16. 
|
7.17. 
| 7.18. 
|
7.19. 
| 7.20. 
|
7.21. 
| 7.22. 
|
7.23. 
| 7.24. 
|
7.25. 
| 7.26. 
|
7.27. 
| 7.28. 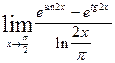
|
7.29. 
| 7.30. 
|
Задача 8. Найти пределы, используя эквивалентные бесконечно малые.
8.1. 
| 8.2. 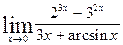
|
8.3. 
| 8.4. 
|
8.5. 
| 8.6. 
|
8.7. 
| 8.8. 
|
8.9. 
| 8.10. 
|
8.11. 
| 8.12. 
|
8.13. 
| 8.14. 
|
8.15. 
| 8.16. 
|
8.17. 
| 8.18. 
|
8.19. 
| 8.20. 
|
8.21. 
| 8.22. 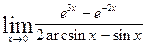
|
8.23. 
| 8.24. 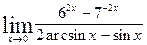
|
8.25. 
| 8.26. 
|
8.27. 
| 8.28. 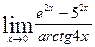
|
8.29. 
| 8.30. 
|
Задача 9. Используя формулы второго замечательного предела и его следствий, найти пределы функций.
9.1. 
| 9.2. 
|
9.3. 
| 9.4. 
|
9.5. 
| 9.6. 
|
9.7. 
| 9.8. 
|
9.9. 
| 9.10. 
|
9.11 
| 9.12. 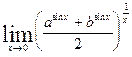
|
9.13. 
| 9.14. 
|
9.15. 
| 9.16. 
|
9.17. 
| 9.18. 
|
9.19. 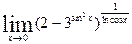
| 9.20. 
|
9.21. 
| 9.22. 
|
9.23. 
| 9.24. 
|
9.25.  (a, b >0) (a, b >0)
| 9.26. 
|
9.27. 
| 9.28. 
|
9.29. 
| 9.30. 
|
Задача 10. Используя правило Лопиталя и эквивалентность, найти следующие пределы.
10.1. a) 
| б) 
|
10.2. а) 
| б) 
|
10.3. а) 
| б) 
|
10.4. а) 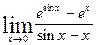
| б) 
|
10.5. а) 
| б) 
|
10.6. а) 
| б) 
|
10.7. а) 
| б) 
|
10.8. а) 
| б) 
|
10.9. а) 
| б) 
|
10.10. а) 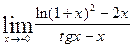
| б) 
|
10.11. а) 
| б) 
|
10.12. а) 
| б) 
|
10.13. 
| б) 
|
10.14. 
| б) 
|
10.15. а) 
| б) 
|
10.16. а) 
| б) 
|
10.17. а) 
| б) 
|
10.18. а) 
| б) 
|
10.19. а) 
| б) 
|
10.20. а) 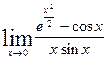
| б) 
|
10.21. а) 
| б) 
|
10.22. а) 
| б) 
|
10.23. а) 
| б) 
|
10.24. а) 
|
б) 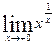
|
10.25. а) 
| б) 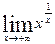
|
10.26. а) 
| б) 
|
10.27. а) 
| б) 
|
10.28. а) 
| б) 
|
10.29. 
| б) 
|
10.30. 
| б) 
|
Задача 11. Применяя формулу Тейлора, вычислить пределы.
11.1 
| 11.2. 
| |
11.3. 
| 11.4. 
| |
11.5. 
| 11.6. 
| |
11.7. 
| 11.8. 
| |
11.9. 
| 11.10. 
| |
11.11. 
| 11.12. 
| |
11.13. 
| 11.14. 
| |
11.15. 
| 11.16. 
| |
11.17. 
| 11.18. 
| |
11.19. 
| 11.20 
| |
11.21. 
| 11.22. 
| |
11.23. 
| 11.24. 
| |
11.25. 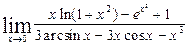
| 11.26. 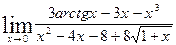
| |
11.27.
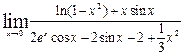
| 11.28. 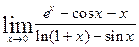
| |
11.29. 
| 11.30. 
| |
Задача 12. Найти точки разрыва, уравнения асимптот и построить схематично график функции.
12.1. а) 
| б) 
| ||
12.2. а) 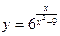
| б) 
| ||
12.3. а) 
| б) 
| ||
12.4. а) 
| б) 
| ||
12.5. а) 
| б) 
| ||
12.6. а) 
| б) 
| ||
12.7. а) 
| б) 
| ||
12.8. а) 
| б) 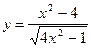
| ||
12.9. а) 
| б) 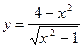
| ||
12.10. а) 
| б) 
| ||
12.11. а) 
| б) 
| ||
12.12. а) 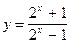
| б) 
| ||
12.13. а) 
| б) 
| ||
12.14. а) 
| б) 
| ||
12.15. а) 
| б) 
| ||
12.16. а) 
| б) 
| ||
12.17. а) 
| б) 
| ||
12.18. а) 
| б) 
| ||
12.19. а) 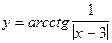
| б) 
| ||
12.20.а) 
| б) 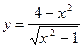
| ||
12.21. а) 
| б) 
| ||
12.22. а) 
| б) 
| ||
12.23. а) 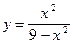
| б) 
| ||
12.24. а) 
| б) 
| ||
12.25. а) 
| б) 
| ||
12.26. а) 
| б) 
| ||
12.27. а) 
| б) 
| ||
12.28. а) 
| б) 
| ||
12.29. а) 
| б) 
| ||
12.30. а) 
| б) 
| ||
§ 4. 2. Индивидуальное домашнее задание по теме: «Производная и ее применение»
Задача 1. Найти первую производную функции:
1.1. 
1.2. 
1.3. 
1.4. 
1.5. 
1.6. 
1.7. 
1.8. 
1.9. 
1.10. 
1.11. 
1.12. 
1.13. 
1.14. 
1.15. 
1.16. 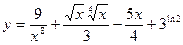
1.17. 
1.18. 
1.19. 
1.20. 
1.21. 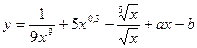
1.22. 
1.23. 
1.24. 
1.25. 
1.26. 
1.27. 
1.28. 
1.29. 
1.30. 
Задача 2. Найти первую производную функции:
2.1.  2.2.
2.2. 
2.3. 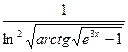 2.4.
2.4. 
2.5.  2.6.
2.6. 
2.7.  2.8
2.8 
2.9.  2.10.
2.10. 
2.11. 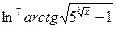 2.12.
2.12. 
2.13.  2.14.
2.14. 
2.15.  2.16.
2.16. 
2.17.  2.18.
2.18. 
2.19. 
2.20. 
2.21. 
2.22. 
2.23. 
2.24. 
2.25. 
2.26. 
2.27. 
2.28. 
2.29. 
2.30. 
Задача 3. Найти первую производную функции:
3.1.  3.2.
3.2. 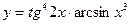
3.3.  3.4.
3.4. 
3.5.  3.6.
3.6. 
3.7.  3.8.
3.8. 
3.9.  3.10.
3.10.  3.11.
3.11.  3.12.
3.12. 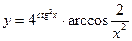
3.13.  3.14.
3.14. 
3.15.  3.16.
3.16. 
3.17. 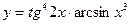 3.18.
3.18. 
3.19.  3.20.
3.20. 
3.21.  3.22.
3.22. 
3.23. 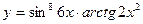 3.24.
3.24. 
3.25.  3.26.
3.26. 
3.27.  3.28.
3.28. 
3.29.  3.30.
3.30. 
Задача 4. Найти первую производную функции:
4.1.  4.2.
4.2. 
4.3.  4.4.
4.4. 
4.5.  4.6.
4.6. 
4.7.  4.8.
4.8. 
4.9.  4.10.
4.10. 
4.11.  4.12.
4.12. 
4.13.  4.14.
4.14. 
4.15.  4.16.
4.16. 
4.17.  4.18.
4.18. 
4.19.  4.20.
4.20. 
4.21.  4.22.
4.22. 
4.23.  4.24.
4.24. 
4.25.  4.26.
4.26. 
4.27.  4.28.
4.28. 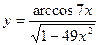
4.29.  4.30.
4.30. 
Задача 5. Найти первую производную функции:
5.1.  5.2.
5.2. 
5.3  5.4.
5.4. 
5.5.  5.6.
5.6. 
5.7.  5.8.
5.8. 
5.9.  5.10.
5.10. 
5.11.  5.12.
5.12. 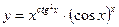
5.13.  5.14.
5.14. 
5.15.  5.16.
5.16. 
5.17.  5.18.
5.18. 
5.19.  5.20.
5.20. 
5.21.  5.22.
5.22. 
5.23  5.24.
5.24. 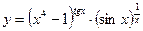
5.25.  5.26.
5.26. 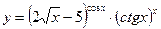
5.27.  5.28.
5.28. 
5.29.  5.30.
5.30. 
Задача 6. Найти первую производную функции:
6.1.  6.2.
6.2. 
6.3.  6.4.
6.4. 
6.5.  6.6.
6.6. 
6.7.  6.8.
6.8. 
6.9.  6.10.
6.10. 
6.11.  6.12.
6.12. 
6.13.






