Факультет естественных наук
Р.Т. ГАЛУСАРЬЯН
Сборник задач и упражнений
по курсу «Высшая математика»
(1-й семестр, часть II)
Обнинск 2008
УДК 51(076)
Галусарьян Р.Т. Сборник задач и упражнений по курсу «Высшая математика», ч. II.  Обнинск: ИАТЭ, 2008.
Обнинск: ИАТЭ, 2008.  76с.
76с.
Во второй части сборника включены вопросы, связанные с элементами комбинаторики, математической индукции и комплексными числами. В сборнике приведены индивидуальные домашние задания (ИДЗ) по темам: 1)Предел функции и непрерывность; 2)Производная. К задачам ИДЗ: Предел функции и непрерывность приведены ответы
Рецензенты: д.ф.-м.н. Е.А.Сатаев,
к. ф.-м. н. А.Г.Слесарев
Темплан 2008, поз 17
© Р.Т.Галусарьян, 2008г.
© Обнинский государственный технический университет атомной энергетики, 2008 г.
Содержание
Предисловие.............................................................................. 4
Глава 3. Введение в анализ
§3.1. Комбинаторика и бином Ньютона ……………………… 5
§3.2. Комплексные числа …………………………………… 13
Глава 4. Индивидуальные домашние задания
§ 4.1. ИДЗ «Предел функции и непрерывность» ………….. 20
§ 4.2. ИДЗ «Производные» ………………………………… 40
Глава 5. Семинары
§5.1. Применение производной при исследовании функции.. 61
§ 5.2. Неопределенный интеграл …………………………… 65
Ответы...................................................................................... 69
Литература................................................................................. 76
Предисловие
Вторая часть сборника задач по курсу «Высшая математика» содержит введение в математический анализ (Глава 3) и индивидуальные домашние задания по теме: «Предел функции и непрерывность» и по теме: «Производная»
Глава 3 содержит следующие темы: комбинаторика, бином Ньютона, математическая индукция и комплексные числа Приведены основные формулы и методы решения задач.
Глава 4 содержит индивидуальные домашние задания по основным темам курса математического анализа, изучаемым в первом семестре
Глава 5 посвящена семинарским занятиям. Приводится перечень основных вопросов, рассматриваемых на семинаре, задачи, которые необходимо решать на семинаре и задачи для самостоятельной работы.
К задачам главы 3 и к задачам ИДЗ «Предел функции» приведены ответы. Для наиболее сложных задач приводятся решения.
Глава 3. Введение в анализ
Комбинаторика и бином Ньютона
Комбинаторика
1. Число перестановок из n элементов равно произведению n последовательных натуральных чисел от 1 до n.
Число перестановок обозначается так:
 или n! (эн-факториал) и вычисляется по формуле:
или n! (эн-факториал) и вычисляется по формуле:
n! =  . (1.1)
. (1.1)
Число размещений (без повторений) из n элементов по к
 равно произведению к последовательных натуральных чисел, наибольшее из которых равно n:
равно произведению к последовательных натуральных чисел, наибольшее из которых равно n: 
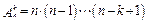 , (1.2)
, (1.2)
 или
или  . (1.3)
. (1.3)
3. Число сочетаний из n элементов по к ( ) определяется по формуле:
) определяется по формуле:
 (1.4)
(1.4)
или  (1.5)
(1.5)
Из формулы (1.5) следует  . (1.6)
. (1.6)
Размещения с повторениями
Пусть из множества Х, состоящего из n элементов, надо составить строку из к элементов, причем каждый элемент в
строке может быть любым элементом из х, т.е. в строке
элементы могут повторяться.
Общее число всех таких строк есть число размещений
из n по k с повторениями: А(n, k) = nk. (1.7)
В рассмотренном случае каждый элемент строки может принимать n значений. Если в строке 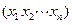 элемент
элемент  может принимать
может принимать 
 значений, элемент
значений, элемент  может принимать
может принимать  значений, то количество всех таких строк определяют по формуле:
значений, то количество всех таких строк определяют по формуле:

 . (1.8)
. (1.8)
Размещения данного состава
Размещением данного состава  из элементов
из элементов
множества  называется всякая строка длиной
называется всякая строка длиной  , составленная из элементов множества X так, что элемент
, составленная из элементов множества X так, что элемент  повторяется
повторяется 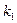 раз, элемент
раз, элемент  повторяется
повторяется  раз,..., элемент
раз,..., элемент  повторяется
повторяется  раз.
раз.
Например, если  то
то  есть
есть
один из вариантов состава 
Число различных размещений состава определяется по формуле:
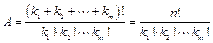 . (1.9)
. (1.9)
Бином Ньютона
Формула бинома Ньютона позволяет любой двучлен (бином) возвести в натуральную степень. Эта формула имеет вид:
 (1.10)
(1.10)
или сокращенно 
В разложении бинома n + 1 членов. Так как  , то
, то
коэффициенты членов разложения, одинаково удаленных от начала и конца, равны между собой. При  получаем формулу для суммы биномиальных коэффициентов:
получаем формулу для суммы биномиальных коэффициентов:
 (1.11)
(1.11)
Обобщением формулы бинома Ньютона является
полиномиальная формула:
 (1.12)
(1.12)
где  и суммирование ведется по всем наборам
и суммирование ведется по всем наборам  .
.
В частности:


Итак, 
 . (1.13)
. (1.13)
3. Формула разложения разностиn-ых степеней 
 (1.14)
(1.14)






