В геометрії, механіці, фізиці часто зустрічається параметричний спосіб задання рівняння, що описує криву на площині чи в просторі. Саму ж лінію можна розглядати як геометричне місце послідовних положень рухомої точки, координати x та y якої є функціями допоміжної змінної 
(часу, швидкості, відстані і т.д.) Допоміжну змінну називають параметром, а рівняння функції – параметричним. Для прикладу, крива на площині визначається двома рівняннями
Похідна заданої функції першого порядку знаходиться за правилом
Друга похідна визначається залежністю
Аналогічним чином можна вивести похідні старших порядів.Розглянемо декілька прикладів для закріплення матеріалу на практиці.
Приклад 1.
Знайти похідні функцій, заданих параметрично.
1)
2)
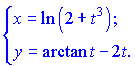
3)
4)
Розв'язок.
1) Обчислимо похідні функції та аргументу за параметром t
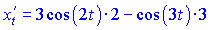
Знайдені значення підставляємо у формулу
В даному випадку, щоб не виносити знак мінус перед дріб, домножили на знаменник та переставили доданки так, щоб першими йшли додатні.
2) Знайдемо похідні за параметром
Обчислюємо значення похідної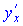 
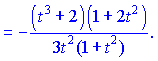
3) Обчислюємо похідні
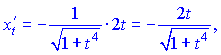
Отримані значення підставимо у формулу для похідної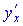 
4) Продиференціюємо функцію та аргумент за параметром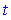 
Отримані значення підставляємо у формулу і спрощуємо чисельник та знаменник на t
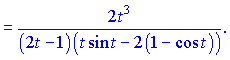
5.Економічний зміст похідної. Похідна вищих порядків
Нехай функція 
виражає кількість виробленої продукції u за час t, і необхідно знайти продуктивність праці в момент 
.
Очевидно, за період часу від до 
кількість виробленої продукції зміниться від значення 
до значення 
. Тоді середня продуктивність праці за цей термін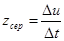 
.
Продуктивність праці в момент можна визначити як граничне значення середньої продуктивності за період часу від до при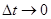 
, тобто 
.
Отже, похідна обсягу виробленої продукції за часом 
є продуктивність праці в момент . У цьому економічний зміст похідної.
У практиці економічних досліджень широке застосування отримали виробничі функції, які використовують для встановлення залежності, наприклад, випуску продукції від витрат ресурсів, витрат виробництва від обсягу продукції, виторгу від проданого товару і т.д. У припущенні диференційованості виробничих функцій важливе значення набувають їхні диференціальні характеристики, пов’язані з поняттям похідної.
Розглянемо похідні для означених типів виробничої функції.
1. Нехай виробнича функція К=К(х) – функція витрат виробництва, що залежить від кількості продукції х. Припустимо, що кількість продукції збільшиться на 
. Кількості продукції 
відповідають витрати виробництва 
. Отже приросту кількості продукції відповідає приріст витрат на виробництво продукції 
.
Середній приріст витрат виробництва є 
. Це приріст витрат виробництва на одиницю кількості продукції. Граничними витратами виробництва називається границя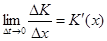 
.
Граничні витрати виробництва збігаються зі швидкістю зміни витрат виробництва. Величина 
характеризує наближено додаткові витрати на виробництво одиниці додаткової продукції.
2. Позначимо 
виторг від продажу х одиниць товару.
Граничним виторгом називається границя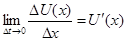 
.
3. Нехай виробнича функція 
встановлює залежність випуску продукції 
від витрат ресурсу х.
Граничним продуктом називається границя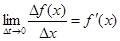 
.
2. Нехай аргумент х функції 
одержав приріст . Тоді значення функції зміняться на величину 
.
Прирости і 
називаються абсолютними приростами аргументу і функції відповідно. Складемо відносні прирости змінних 
і 
.
Границя відношення відносного приросту функції до відповідного відносного приросту аргументу при умові, що абсолютний приріст аргументу прямує до нуля, називається еластичністю функції 
по змінній х і позначаються символом
.
.
Еластичність 
показує наближено, на скільки відсотків зміниться значення функції у разі зміни незалежної змінної х на 1% (з х до х+0,01х).
Формулу можна переписати у вигляді: 
.
Це означає, що для функцій випуску еластичність дорівнює відношенню граничного виробництва ресурсу до його середнього значення виробництва.
Приклад. Знайти 
, якщо 
.
Розв’язок. Еластичність заданої функції обчислюємо за формулою:
Знайдемо .
.
Це означає, що при збільшенні х з 2 до 2,02 значення функції зростає на 0,6%.
1. Якщо 
, то функція називається нееластичною (відносний її приріст спадає).
2. Якщо 
, то функція називається еластичною (відносний її приріст зростає).
Властивості:
1) 
;
2) 
;
3) 
Еластичність елементарних функцій
1. Еластичність степеневої функції 
стала і дорівнює показнику степеня 
.
Справді: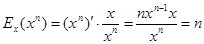 
2. Еластичність показникової функції 
пропорційна до х.
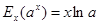
Справді:
.
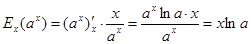3. Еластичність лінійної функції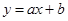 
.
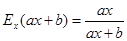Справді:
.
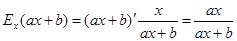Похідні вищих порядків
Під похідною вищих порядків розуміють диференціювання функції більше ніж один раз. Якщо похідну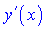 
повторно диференціювати, то одержимо похідну другого порядку, або другу похідну функції 
, і вона позначається 
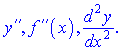
Похідна третього порядку матиме вигляд
Аналагічно отримують формули для знаходження похідних вищих порядків. При знаходженні похідної 
порядку необхідно знати похідну 
-го порядку. Вийняток становлять функції, для яких можна помітити тенденцію зміни похідних. Це степеневі, деякі тригонометричні та експоненціальні функції:
В інших випадках, для знаходження похідних вищих порядків від заданої функції потрібно послідовно знаходити всі її похідні нижчих порядків. Для практичного засвоєння матеріалу розглянемо приклади.
Приклад 1.
Обчислити похідні другого порядку
1)
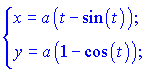
2) 
3) 
4) 
Розв'язок.
1) За правилами диференціювання параметричних функцій маємо
Застосуємо до заданої функції. Знайдемо похідну
Диференціюємо другий раз. За правилом диференціювання отримаємо
За формулою обчисюємо 
2) Визначаємо першу похідну для функції
Обчислюємо другу похідну
3) Обчислимо першу похідну
а потім другу
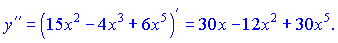
При знаходженні похідної другого і вищих порядків для даного прикладу і йому подібних можна користуватися наступним правилами:
1) якщо степінь функції менший порядку похідної 
, то даний доданок вкладу не дає
2) всі старші степеня дають вклад
За такою схемою другу похідну можна було знайти так:
Для практики другий спосіб ефективніший, особливо якщо потрібно знайти похідні набагато вищих порядків ніж другий.
3) Похідну функції 
першого порядку матиме вигляд
другого порядку
По аналогії можна вивести формулу для похідної експоненціальної функції порядку
Основні формули диференціювання:
1. 
,a є k
2. 
3. 
,(a= 
)
4. 
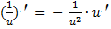,(a= -1)
5. 
6. 
7. (
= 
8. 
9. 
=cos u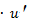 
10. 
11. 
12. 
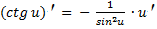
13. 
14. 
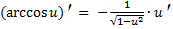
15. 
16. 
Тема 8:Дослідження функції на екстремум.Дослідження функції.
1. Означення. Нехай функція f(x;y) визначена в деякому околі точки(a,b).Точка(a,b)називається точкою мінімуму (максимумом) цієї функції в точці (a;b), якщо існує такий окіл точки (a;b), що для всіх точок (x;y) з цього околу, відмінних від точки (a;b), виконується нерівність f(a;b)<f(x;y)(f(a;b)<f(x;y)).
Точки мінімуму і максимуму функції називають її точками екстрему, а максимум та мінімум функції в точці – її екстремумом у цій точці.
Теорема (необхідна умова екстремуму). Якщо точка (a;b) є точкою екстремуму функції f (x;y) і якщо в цій точці існують частинні похідні функції по змінних x та y, то ці похідні дорівнюють 0: 
, 
.
Доведемо, наприклад, що . Для доведення зафіксуємо значення змінної y, поклавши y=b. Дістанемо функцію z=f(x,b) однієї змінної х, що має в точці х=а екстремум і похідну, яка є частиною похідної 
. Згідно з теоремою Тейлора ця похідна функції однієї змінної дорівнює 0. Таким чином, . Рівність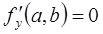 
встановлюється аналогічно.
Точка простору R2, в якій існують обидві частинні похідні якоїсь функції двох змінних, кожна з яких дорівнює нулю, називається стаціонарною для цієї функції.
Теорема стверджує, що всі точки екстремуму функції двох змінних, яка має частинні похідні по обох змінних в деякій області простору R2, утворюють підмножину множини її стаціонарних точок.
Теорема (достатні умови екстремуму). Нехай функція f (x;y) в деякому околі своєї стаціонарної точки (a;b) має неперервні в цій частині похідні другого порядку.
Якщо 
, то точка (a;b) є точкою екстремуму функції f (x;y), при чому точкою мінімуму, якщо 
, і точкою максимуму, якщо 
. Якщо ж 
, то точка (a;b) не є точкою екстремуму функції f (x;y)
Приклад:
Дослідити на екстремум функції 
.
Ця функція визначена і має неперервні всі частини похідні першого та другого порядків в R2. Її частинні похідні першого порядку мають вигляд 
.
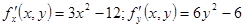Стаціонарні точки функції визначаємо з системи
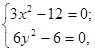, яка рівносильна системі 
Отже, досліджувана функція має чотири стаціонарні точки: (-2;1), (2;-1), (-2;-1),(2;1). Знаходимо частинні похідні другого порядку:
.
Обчисливши значення
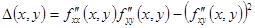
Дістанемо
Таким чином, точки (-2;-1),(2;1) є точками екстремуму заданої функції. Оскільки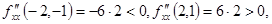 
точка (-2;-1) є точкою максимуму функції , а точка (2;1) – точкою мінімуму. Залишилося знайти екстремуми: максимум функції f (x;y) у точці (-2;-1) становить f (-2,-1)=21, а мінімум у точці (2;1) – f (2,1)=-19
