Відповідністю між множинами A і B називається будь-яка підмножина C Í A ´ B. Якщо (a,b)Î C, то кажуть, що елемент b відповідає елементу a при відповідності C.
Оскільки відповідності є множинами, то для їхнього задання використовують ті самі методи, що й для довільних множин.
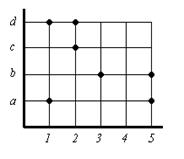
Крім того, відповідність можна задавати (або ілюструвати) за допомогою так званого графіка відповідності. Нехай А= { 1,2,3,4,5 } і B= { a,b,c,d }, а C= {(1,a), (1,d), (2,с), (2,d), (3,b), (5,а), (5,b)} - відповідність між A і B. Позначимо через 1,2,3,4,5 вертикальні прямі, а через a,b,c,d - горизонтальні прямі на координатній площині (рис.1.3а). Тоді виділені вузли на перетині цих прямих позначають елементи відповідності C і утворюють графік відповідності
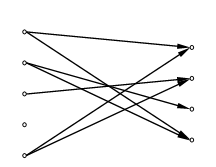
Зручним методом задання невеликих скінченних відповідностей є діаграма або граф відповідності. В одній колонці розташовують точки, позначені елементами множини A, у колонці праворуч - точки, позначені елементами множини B. З точки a першої колонки проводимо стрілку в точку b другої колонки тоді і тільки тоді, коли пара (a,b) належить заданій відповідності. На рис.1.3б зображено діаграму відповідності C із попереднього абзацу.
Нехай C деяка відповідність. Множина Pr1 C називається областю визначення, а множина Pr2 С - областю значень відповідності C.
Образом елемента a ÎPr1 C при відповідності C називається множина всіх елементів b ÎPr2 C, які відповідають елементу a; позначається C(a). Прообразом елемента b ÎPr2 C при відповідності C називається множина всіх тих елементів a ÎPr1 C, яким відповідає елемент b; позначається
C -1 (b). Якщо D ÍPr1 C, то образом множини D при відповідності C називається об’єднання образів усіх елементів із D; позначається C(D). Аналогічно означається прообраз деякої множини G Í Pr2 C; позначається C -1 (G).
а) б)
Рис.1.3
Оскільки відповідності є множинами, то до довільних відповідностей можуть бути застосовані всі відомі теоретико-множинні операції: об’єднання, перетин, різниця тощо.
Додатково для відповідностей введемо дві специфічні операції. Відповідністю, оберненою до заданої відповідності C між множинами A і B, називається відповідність D між множинами B і A така, що D= { (b,a) | (a,b)Î C }. Відповідність, обернену до відповідності C, позначають C - 1.
Якщо задано відповідності C Í A ´ B і D Í B ´ F, то композицією (суперпозицією, добутком) відповідностей C і D (позначається C ° D) називається відповідність H між множинами A і F така, що
H= {(a,b) | існує елемент c Î B, для якого (a,c)Î C і (c,b)Î D }.
Розглянемо окремі важливі випадки відповідностей C між множинами A і B.
Якщо Pr1 C=A, то відповідність C називається всюди або скрізь визначеною. У противному разі відповідність називається частковою.
Відповідність f Í A ´ B називається функціональною відповідністю, або функцією з A в B, якщо кожному елементові a ÎPr1 f відповідає тільки один елемент з Pr2 f, тобто образом кожного елемента a ÎPr1 f є єдиний елемент b з Pr2 f. Якщо f - функція з A в B, то кажуть, що функція має тип A ® B і позначають f: A ® B або A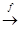 
B.
Всюди визначена функціональна відповідність f Í A ´ B називається відображенням з A в B і записується як і функція f:A ® B або A 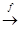B. Відображення називають також усюди або скрізь визначеними функціями.
Відображення типу A ® A називають перетвореннями множини A.
Через BA позначається множина всіх відображень з A в B.
Оскільки функція і відображення є окремими випадками відповідності, то для них мають місце всі наведені вище означення: поняття областей визначення та значень, поняття образу та прообразу елементів і множин тощо. Зокрема, для функції f елементи множини Pr1 f називають аргументами функції, образ f (a) елемента a ÎPr1 f називають значенням функції f на a.
Відповідність C називається сюр’єктивною (сюр’єкцією), або відповідністю на множину B, якщо Pr2 C =B.
Відповідність C називається ін’єктивною (ін’єкцією), або різнозначною відповідністю, якщо для кожного елемента b ÎPr2 C його прообраз C - 1(b) складається тільки з одного елемента. Іншими словами, різним елементам множини A відповідають різні елементи множини B. Іноді ін’єкцію називають 1-1 відповідністю.
Відображення, яке є одночасно сюр’єктивним та ін’єктивним, називається бієктивним, або бієкцією. Бієктивні відображення називають часто також взаємно однозначними відображеннями або взаємно однозначними відповідностями між множинами A і B.
Таким чином, відповідність є взаємно однозначною тоді і лише тоді, коли вона функціональна, всюди визначена, сюр’єктивна та ін’єктивна.
Відповідність iA = { (a,a) | a Î A } називається тотожним перетворенням, діагональною відповідністю або діагоналлю в A.
Взаємно однозначне відображення з A в A називають підстановкою множини A.
Для довільної відповідності C між A і A позначимо через C(n) відповідність C ° C ° ... ° C (n входжень літери C). Вважатимемо C(0)=iA і C(1)=C.
