Алгебраические критерии устойчивости основаны на закономерностях, связывающих отрицательность всех действительных частей корней характеристического уравнения (х. у.) со знаком коэффициента этого уравнения и некоторых функций от коэффициента.
4.7.1 Критерий Гурвица
Он устанавливает соотношение между коэффициентами x, y в форме неравенств, соблюдение которых является необходимым и достаточным условием устойчивости системы любого порядка.
Система неравенств Гурвица n-ого порядка. По главной диагонали матрицы Гурвица располагаются коэффициенты x, y в порядке их нумерации (с 
по 
). В строках помещаются поочередно коэффициенты только с нечетными или только с четными числами (включая и коэффициент 
), причем влево от диагонали с уменьшающимися, а вправо – с увеличивающимися индексами. Все недостающие коэффициенты с индексами меньше 0 и больше n заменяются нулями
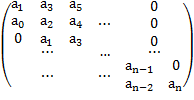
Для соблюдении устойчивости требуется, чтобы все диагональные миноры матрицы были положительны при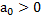 
. Диагональные миноры получаются отчеркиванием их слева и сверху. Последний определитель 
включает в себя всю матрицу Гурвица. Если его раскрыть по элементам последнего столбца, то
.
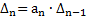Если система автоматического управления неустойчива, т.е.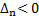 
, то можно выявить характер неустойчивости. Система будет неустойчива апериодически пр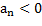и 
и 
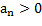и будет неустойчива колебательно, если 
и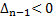 
. Граница устойчивости определяется условием 
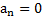при (апериодической устойчивости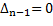) и 
при 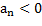(колебательной устойчивости).
4.7.2 Критерий Рауса
Он удобен для системы высокого порядка. Из коэффициентов x, y
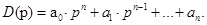
Составляется таблица Рауса с (n+1) числом строк по следующим правилам: элементами первой строки являются все коэффициенты с четными индексами, а элементами второй строки – нечетными индексами. Элементы каждой следующей строки находятся по формуле
где k – номер столбца, i - номер строки, в которой находится коэффициент
Таблица Раусса
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| 
|
| 
| 
| 
| 
|
| 
| 
| 
| 
|
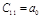
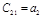
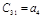
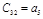
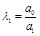
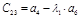
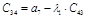
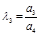
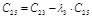
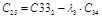
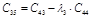
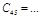
Требование устойчивости по Раусу: для тог, чтобы система была устойчива, необходимо и достаточно, чтобы все коэффициенты первого столбца были положительны при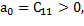 
т.е.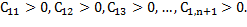 
Число перемен знака в первом столбце таблицы Рауса указывает на число неустойчивых корней x, y, расположенных в правой полуплоскости.
4.7.3 Критерий Михайлова
Критерий устойчивости Михайлова относится к частотным критериям, в основу которых положен принцип аргумента. Требование устойчивости по критерию Михайлова, формулируется в следующем виде: система будет устойчива тогда и только тогда, когда при возрастании γ от 0 до +∞ характеристический вектор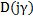 
повернется в положительном направлении на угол 
, где n – степень x,y, если при увеличении γ от 0 до +∞ годограф x,y, начинаясь с положительной части действительной оси, проходит последовательно в положительном направлении n квадрантов.
Оценка устойчивости системы по критерию Михайлова производится в следующем порядке.
Пусть дано характеристического уравнение системы n-ого порядка
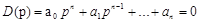
где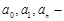 
коэффициенты x,y
в данное уравнение подставляем значение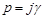 
. Получим уравнение характеристической кривой
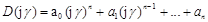
Полученное уравнение разделим на действительную и мнимую части
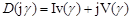
Задаемся значением γ в пределах от 0 до +∞ и вычисляем значения Iv(γ) и jV(γ). Количество частот γ при этом берется таким, какое необходимо для построения годогафа x,y.
Для каждого значения частоты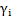 
на комплексной плоскости в координатах W(γ) и j(γ) откладывается по оси абсцисс W(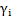), а по оси ординат V(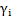). Получим точку, соответствующую концу вектора D(jγ). По совокупности этих точек при изменении γ от 0 до +∞ строится характеристическая кривая, или годограф x,y и производится оценка устойчивости системы.
Алгебраические и частотные критерии устойчивости достаточно полно изложены в [1], которой и следует пользоваться при выполнении задачи №3.
