Программой предусматривается выполнение двух контрольных заданий. В первом контрольном задании решаются задачи № 1 и 2 на применение алгебры матриц в задачах электроснабжения. Во втором контрольном задании решаются задачи № 3 и 4, соответствующие разделам 2.2 и 2.4 программы дисциплины.
Каждая задача в контрольных заданиях включает в себя 10 вариантов. Номер варианта выбирается в соответствии с последней цифрой шифра зачетной книжки студента. Студенты, имеющие последней цифрой шифра «1», выполняют первый вариант, при последней цифре «0» - десятый вариант.
Контрольные задания выполняются на листах ученических тетрадей. Разрешается писать на обеих сторонах листа. Рисунки в работе могут выполняться как на самих листах ученических тетрадей, так и на миллиметровой бумаге, имеющей размеры листа ученической тетради. Листы тетради должны иметь поля и быть пронумерованы. Каждая задача должна начинаться с новой страницы, иметь подробное условие задачи и содержать необходимые пояснения по ее решению. Исправления, вносимые по решению задач, должны быть аккуратны и разборчивы. В конце контрольного задания помещается список использованной литературы. Оформленная работа должна иметь подпись студента, дату выполнения, шифр зачетной книжки, точный домашний адрес. Допускается оформление контрольных заданий № 1 и 2 в одной тетради.
Задача № 1. Для графа электрической сети, приведенного на рисунке 3.1, записать первую и вторую матрицу соединения (инциденций). Нарисовать исходный граф и два из возможных вариантов деления его на дерево и хорды. Под каждым их рисунков сделать соответствующую надпись «дерево» или хорды».
Варианты заданий приведены на рисунке 3.1.


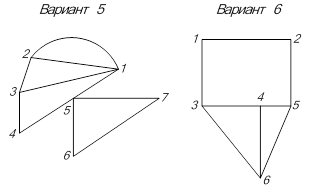


Рисунок 3.1 – Варианты заданий к задаче № 1
Перед составлением матриц соединений необходимо пронумеровать ветви, задаться их направлением, а также выбрать независимые замкнутые контуры и направление их обхода.
Первую матрицу соединений составить только для независимых узлов, т.е. за исключением базисного. В качестве базисного узла принять узел 1.
При выполнении задачи рекомендуется изучить § 1-3/1/.
Задача № 2. Найти узловые напряжения и токораспределение в схеме, показанной на рисунке 3.2, методом узловых напряжений, используя обращение матрицы узловых проводимостей и один из традиционных способов решения уравнений (см. таблицу 3.1). За балансирующий и базисный узел принять узел 0, считая, что 
Данные о задающих токах приведены в таблице 3.2.
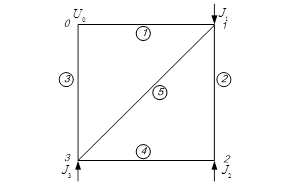
Рисунок 3.2 – Схема электрической сети
Таблица 3.1 – Варианты заданий
| Варианты заданий | Метод решения задачи |
| Простой итерации | |
| Зейделя | |
| Ньютона | |
| Зейделя | |
| Ньютона | |
| Простой итерации | |
| Ньютона | |
| Зейделя | |
| Простой итерации | |
| Ньютона |
Таблица 3.2 – Данные о задающих токах
| № уз | Значения задающих токов в узлах, А | |||||||||
| Варианты заданий | ||||||||||
| 1 2 3 | -140 -120 0 | -125 -130 -115 | -115 -130 -130 | 0 -150 -140 | -145 -125 -110 | -115 -120 -120 | -125 0 -165 | -140 -130 -150 | -125 -125 -130 | -110 -120 -130 |
Сопротивление ветвей принять: 
Для решения задачи указанными методами необходимо вначале определить матрицу узловых проводимостей. Порядок ее получения приведен в § 1-4/1/, а также в разделе 4.2 данных указаний.
Задача № 3. Система автоматического регулирования описывается характеристическим уравнением четвертого порядка:

Дать оценку устойчивости данной системы, используя критерии Гурвица, Рауса и путем построения кривой Михайлова. Выявить характер неустойчивости (апериодический или колебательный) в случае неустойчивости системы.
Значения коэффициентов характеристического уравнения системы приводятся в таблице 3.3.
Таблица 3.3 – Данные о коэффициентах характеристического уравнения системы
| Варианты заданий | ||||||||||

| 0,1 | 0,5 | 2,0 | 0,3 | 1,7 | 2,4 | 0,05 | 0,7 | 0,17 | 2,1 |

| 0,5 | 0,9 | 3,6 | 0,2 | 1,7 | 0,65 | 9,4 | |||

| 4,1 | 5,2 | 3,8 | 4,2 | 20,0 | |||||

| 0,5 | 3,0 | 1,8 | |||||||

| 1,8 | 1,5 | 1,1 | 0,3 | 1,5 | 0,9 |
При выполнении данной задачи рекомендуется предварительно познакомиться с теоретическим положениями рассматриваемых вопросов (см. § 4-7, § 5-1, § 5-5/1/) и пояснениями, приведенными в разделе 4.7 данных указаний.
Задача № 4. Найти минимум целевой функции задачи линейного программирования, заданной в канонической форме. Задачу решить комплексным методом.
Уравнения функций цели и систем ограничений по вариантам приведены в таблице 3.4.
Таблица3.4 – Уравнения функции цели и систем ограничений
| № | Целевая функция | Система ограничений | Граничные условия |

| 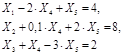
| 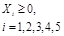
| |

| 
| 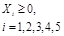
| |

| 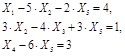
| 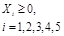
| |

| 
| 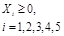
| |

| 
| 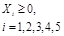
| |

| 
| 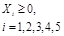
| |

| 
| 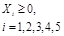
| |
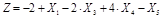
| 
| 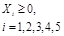
|
Продолжение таблицы 3.4
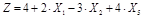
| 
| 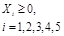
| |

| 
| 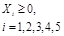
|




