2.1 Коротка характеристика задач електростатики та методів
їхнього розв’язування
Самими простими задачами електростатики є задачі, коли задано закон зміни потенціалу 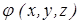 в просторі і необхідно знайти закони розподілу напруженості поля
в просторі і необхідно знайти закони розподілу напруженості поля 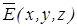 і об’ємної густини зарядів
і об’ємної густини зарядів  , які створили дане поле. Такого роду задачі розв’язуються дворазовим диференціюванням потенціальної функції згідно з рівняннями Пуассона.
, які створили дане поле. Такого роду задачі розв’язуються дворазовим диференціюванням потенціальної функції згідно з рівняннями Пуассона.
Більш складними є зворотні задачі, коли для заданого закону розподілу вільних зарядів у просторі  необхідно визначити залежність зміни напруженості
необхідно визначити залежність зміни напруженості 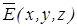 і потенціалу
і потенціалу 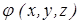 від координат. Розв’язування таких задач зводиться до розв’язування диференціальних рівнянь Пуассона або Лапласа з використанням граничних умов.
від координат. Розв’язування таких задач зводиться до розв’язування диференціальних рівнянь Пуассона або Лапласа з використанням граничних умов.
Досить часто зустрічаються задачі, коли задано розміри і просторове розташування тіл, їхні заряди або їхні потенціали, а необхідно визначити закономірність зміни напруженості поля і потенціалу для всіх точок простору.
В окремих випадках, коли поле, створене тілами, має який-небудь вид симетрії (циліндрична, сферична та ін.), такі задачі розв’язуються за допомогою теореми Гаусса. При цьому необхідно враховувати, що, якщо середовище, в якому створено поле, є неоднорідним (різні діелектричні проникності), то зручно розв’язок отримувати для кожної області окремо, узгоджуючи розв’язки один відносно одного таким чином, щоб виконувались граничні умови.
Розв’язування останнього типу задач в загальному вигляді, для довільної конфігурації заряджених тіл, є досить складним. В таких випадках застосовують спеціальні методи:
- метод зображень;
- метод розділу змінних;
- чисельні методи;
- метод конформних перетворень;
- графічні методи;
- методи моделювання та ін.
2.2 Застосування співвідношень, які пов’язані з законом Кулона
і методом накладання
Приклад 2.1
Два позитивних точкових заряди 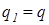 і
і 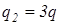 (рис.2.1) розташовані на відстані
(рис.2.1) розташовані на відстані 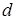 один відносно одного.
один відносно одного.

Рисунок 2.1
Знайти на прямій, яка з’єднує ці заряди, точку 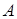 , напруженість в якій дорівнює нулю, і точку
, напруженість в якій дорівнює нулю, і точку 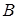 , в якій напруженості, що створені кожним зарядом рівні і однаково направлені. Знайти також потенціали цих точок.
, в якій напруженості, що створені кожним зарядом рівні і однаково направлені. Знайти також потенціали цих точок.
Розв’язування. В зв’язку з тим, що напруженість поля направлена від позитивного заряду, то точка 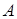 повинна знаходитись між зарядами
повинна знаходитись між зарядами  та
та 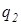 і ближче до меншого заряду
і ближче до меншого заряду  . Якщо позначити відстань між зарядом
. Якщо позначити відстань між зарядом  і точкою
і точкою 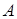 через
через 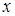 , то повинна виконуватись рівність
, то повинна виконуватись рівність
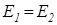 .
.
Величина напруженості поля від точкового заряду визначається за (1.4), тому
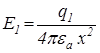 ;
; 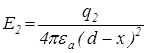 .
.
Врахувавши те, що за умовою задачі 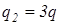 , отримаємо
, отримаємо
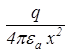 =
= 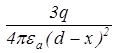 .
.
Після перетворень отримаємо квадратне рівняння
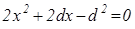 .
.
Розв’язком цього рівняння є два значення 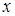
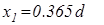 і
і 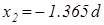 .
.
Перше значення визначає положення точки 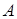 на відстані
на відстані 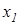 від заряду
від заряду 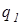 вправо, друге значення характеризує положення точки
вправо, друге значення характеризує положення точки 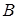 на відстані
на відстані 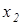 вліво від заряду
вліво від заряду 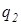 (рис.2.1).
(рис.2.1).
Застосувавши принцип накладання і (1.35) для визначення потенціалу від точкового заряду, отримаємо потенціали в точках 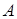 і
і 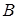
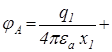
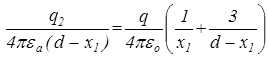 ,
,
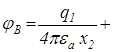
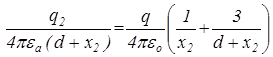 .
.
Приклад 2.2
Визначити силу, яка діє в пустоті на заряд 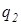 і напруженість поля в точці
і напруженість поля в точці 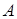 (рис.2.2), якщо задано: точкові заряди
(рис.2.2), якщо задано: точкові заряди 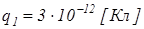 ,
, 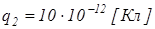 ,
, 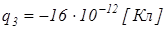 , відстань
, відстань 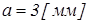 ,
, 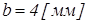 ,
, 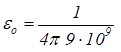 [Ф/м].
[Ф/м].
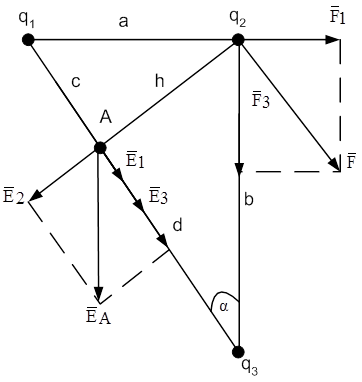
Рисунок 2.2
Розв’язування. На заряд 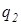 діє дві сили – від заряду
діє дві сили – від заряду  і від заряду
і від заряду 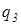 .За законом Кулона
.За законом Кулона
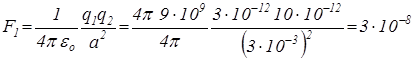 [Н],
[Н],
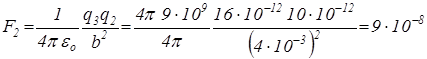 [Н].
[Н].
Напрямок дії сил показано на рис.2.2. В зв’язку з тим, що прямі а і  розташовані під прямим кутом, то результуюча сила дорівнює
розташовані під прямим кутом, то результуюча сила дорівнює
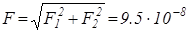 [Н].
[Н].
Для визначення напруженості в точці А необхідно знайти відстані c,h і d. З прямокутного трикутника знаходимо
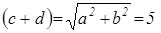 [мм],
[мм], 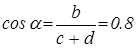 .
.
Звідси
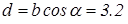 [мм], с=1.8 [мм],
[мм], с=1.8 [мм], 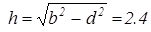 [мм].
[мм].
Знаходимо напруженість в точці А від кожного заряду
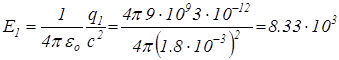 [В/м],
[В/м],
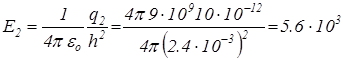 [В/м],
[В/м],
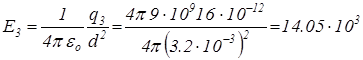 [В/м],
[В/м],
В зв’язку з тим, що заряд 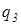 від’ємний, то напруженості
від’ємний, то напруженості  і
і 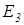 направлені в одну сторону, тому результуюча напруженість в точці А визначається за теоремою Піфагора
направлені в одну сторону, тому результуюча напруженість в точці А визначається за теоремою Піфагора
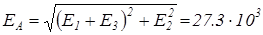 [В/м].
[В/м].
Приклад 2.3
В електричному полі позитивного точкового заряду 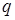 напруга між точками А і В дорівнює 25 [В] (рис.2.3). Визначити величину і напрямок напруженості поля в точці С, якщо а=3[см], b=7[см], d=5[см].
напруга між точками А і В дорівнює 25 [В] (рис.2.3). Визначити величину і напрямок напруженості поля в точці С, якщо а=3[см], b=7[см], d=5[см].
Розв’язування. Напругу в електростатичному полі знаходимо як різницю потенціалів
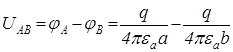 .
.
Звідси знаходимо величину заряду
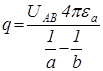 .
.
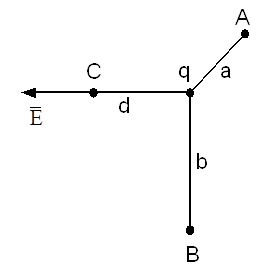
Рисунок 2.3
Напруженість в точці С
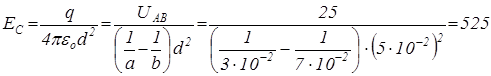 [В/м].
[В/м].
Направлена напруженість по прямій d в сторону від позитивного заряду  .
.
Приклад 2.4
Визначити в точці А напруженість поля, створеного зарядом  тонкого прямолінійного тіла, геометричні розміри якого наведені на рис.2.4.
тонкого прямолінійного тіла, геометричні розміри якого наведені на рис.2.4.
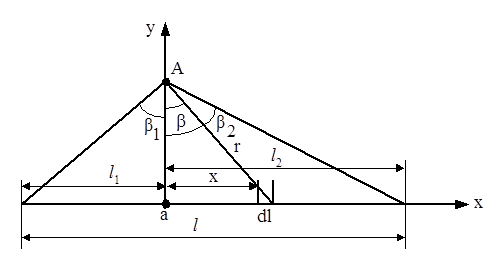
Рисунок 2.4
Розв’язування. Припустимо, що тіло заряджене рівномірно з лінійною густиною заряду 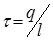 .
.
Будемо розв’язувати задачу в прямокутній системі координат і для знаходження напруженості електричного поля використаємо (1.14)
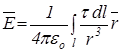 . (2.1)
. (2.1)
Виділимо елемент 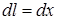 на відстані
на відстані  від точки А. Вектор
від точки А. Вектор 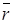 направлений від елементу
направлений від елементу 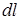 до точки А, тому в прямокутній системі координат
до точки А, тому в прямокутній системі координат
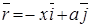 ,
, 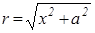 .
.
Підставимо ці значення в (2.1) та врахуємо, що межами інтегрування є значення – l1 і l2. Тоді
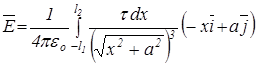 .
.
Ввівши нову змінну – кут 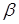 , зручно взяти даний інтеграл. В зв’язку з тим, що
, зручно взяти даний інтеграл. В зв’язку з тим, що
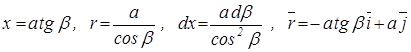 ,
,
то
 =
=
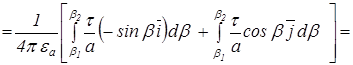
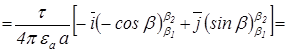
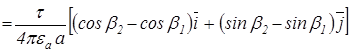 . (2.2)
. (2.2)
Вираз (2.2) показує, що напруженість поля в точці А має складові по осі х
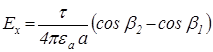
і по осі y
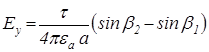 .
.
Величина загальної напруженості
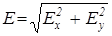 .
.
Для випадку, коли довжина зарядженого тіла l значно більша відстані a 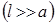 , то
, то 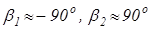 і
і
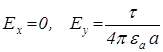 ,
,
тобто напруженість поля направлена перпендикулярно довгому зарядженому тілу, а її величина визначається
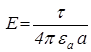 . (2.3)
. (2.3)






