С помощью графиков перемещений, скоростей и ускорений какой-либо точки можно проследить изменение кинематических параметров точки за полный цикл движения механизма. В практических задачах теории механизмов каждая кинематическая диаграмма представляет собой графическое изображение изменения одного из кинематических параметров звена: перемещения, скорости или ускорения точки звена исследуемого механизма в функции времени или перемещения ведущего звена механизма, т.е. в функции обобщенной координаты.
Имея один из графиков, путем графического дифференцирования или интегрирования можно получить два остальных, так как между перемещением, скорости и ускорением точки существуют следующие кинематические зависимости:
 ,
, 
Зависимость перемещения (линейного или углового) выходного (рабочего) звена от обобщенной координаты  или
или  называется функцией положения механизма, а производные функции положения по обобщенной координате – его передаточными функциями.
называется функцией положения механизма, а производные функции положения по обобщенной координате – его передаточными функциями.
| Кинематические функции | Передаточные функции |
1. Линейное перемещение
 (м)
Угловое перемещение (м)
Угловое перемещение
 (рад) (рад)
| 1. Линейная функция положении
 (мм)
Угловая функция положении (мм)
Угловая функция положении

|
2. Линейная скорость точки
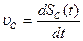 (м/с)
Угловая скорость звена (м/с)
Угловая скорость звена
 (с (с  ) )
| 2. Аналог линейной скорости
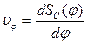 (м)
Аналог угловой скорости (м)
Аналог угловой скорости

|
3. Линейное ускорение точки
 (м/с²)
Угловое ускорение звена (м/с²)
Угловое ускорение звена
 (с (с  ) )
| 3. Аналог линейного ускорения точки
 (м)
Аналог углового ускорения звена (м)
Аналог углового ускорения звена
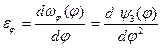 (безразмерная) (безразмерная)
|
Кинематические и передаточные функции связаны следующим образом:
Движение ведущего звена в основном является вращательным и описывается уравнением углового перемещения  и соответственно угловая скорость и ускорение определяются соотношениями:
и соответственно угловая скорость и ускорение определяются соотношениями:
 ,
, 
Так как законы движения ведущих звеньев заданы, будем считать эти параметры определенными. Поэтому при кинематическом исследовании механизмов скорости и ускорения ведомых звеньев и точек, им принадлежащих, удобно выражать в функции поворота  или перемещения
или перемещения  ведущего звена.
ведущего звена.
Если угол поворота 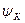 какого-либо звена к определен в виде функции
какого-либо звена к определен в виде функции
 ,
,
то угловая скорость 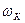 этого звена может быть представлена в следующем виде:
этого звена может быть представлена в следующем виде:
 ;
;
обозначим через 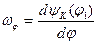 , она величина безразмерная, называется аналогом угловой скорости звена к
, она величина безразмерная, называется аналогом угловой скорости звена к

где  - угловая скорость ведущего звена.
- угловая скорость ведущего звена.
Дифференцируя выражение угловой скорости звена к по времени, получим величину углового ускорения  звена к:
звена к:

Если вращательное движение ведущего звена равномерное, т.е.  , то
, то
 ,
,
Следовательно

где  - величина безразмерная, называется аналогом углового ускорения звена к.
- величина безразмерная, называется аналогом углового ускорения звена к.
Аналогично могут быть получены уравнения для линейной скорости и линейного ускорения какой-либо точки С звена к, с помощью выражении аналога линейной скорости и линейного ускорения точки С.
 ,
,
где  , (м) - аналог линейной скорости точки, имеющий размерность длины.
, (м) - аналог линейной скорости точки, имеющий размерность длины.
 ,
,
где  , (м) – аналог линейного ускорения, имеющий размерность также длины.
, (м) – аналог линейного ускорения, имеющий размерность также длины.
В случае равномерного движения ведущего звена,  его время движения t, угол поворота
его время движения t, угол поворота  , величины
, величины  и
и 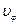 ,
,  и
и  за один цикл (один полный оборот) будут пропорциональными. При этом диаграммы аналогов скоростей и ускорений могут служить диаграммами действительных скоростей и ускорений в разных масштабах.
за один цикл (один полный оборот) будут пропорциональными. При этом диаграммы аналогов скоростей и ускорений могут служить диаграммами действительных скоростей и ускорений в разных масштабах.
Существуют несколько методов графического дифференцирования. Предпочтительным из них является метод касательных, основанный на геометрический смысл производной функции.
Метод касательных
Из плана положений начиная с крайнего правого положения точки  путем замера определяем отрезки
путем замера определяем отрезки  ,
,  ,
,  ,…, соответствующие в масштабе
,…, соответствующие в масштабе  перемещению точки С в каждом рассматриваемом положений (0-12), для углового перемещения рабочего звена 3 определяем угол поворота ψ, замером углов
перемещению точки С в каждом рассматриваемом положений (0-12), для углового перемещения рабочего звена 3 определяем угол поворота ψ, замером углов  Таким образом, для рабочего звена 3 линейное перемещение определяется
Таким образом, для рабочего звена 3 линейное перемещение определяется
 (м) (
(м) ( )
)
угловое перемещение:
 (рад) (
(рад) ( )
)
Необходимо построить диаграмму перемещения рабочего звена 3  или
или 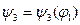 . Выбираем систему координат, по оси абсцисс откладываем отрезок (0-12) в масштабе
. Выбираем систему координат, по оси абсцисс откладываем отрезок (0-12) в масштабе
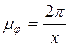 (
( )
)
где х – длина отрезка на оси абсцисс, выбранная произвольно, например для удобства х =180 мм, представляющая один полный оборот ведущего звена, по оси ординат откладываем перемещения рабочего звена 3
 или
или 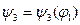 ,
,
соответственно произвольно выбранном масштабе, желательно
 или
или  .
.
Тогда ординаты перемещения звена 3 в каждом положений определяется
 (мм) или
(мм) или  (мм).
(мм).
Соединяем плавной кривой полученные точки ординаты и это является диаграммой перемещения рабочего звена 3.
Для построения диаграммы аналога линейной скорости точки С
 (м)
(м)
или аналога угловой скорости звена 3

пользуемся методом касательных, сущность которого заключается в следующем: выбираем систему координат для функции  или
или  с общей осью ординат диаграммы перемещения. Ось абсцисс этой системы продолжаем влево и откладываем отрезок
с общей осью ординат диаграммы перемещения. Ось абсцисс этой системы продолжаем влево и откладываем отрезок  равный
равный  (мм) – произвольно. Далее в точках 0, 1', 2', 3', … кривой
(мм) – произвольно. Далее в точках 0, 1', 2', 3', … кривой  проводим касательные (рис. 10, а), а через точку
проводим касательные (рис. 10, а), а через точку  - лучи
- лучи  (рис. 10, б) параллельные проведенным касательным.
(рис. 10, б) параллельные проведенным касательным.
Лучи 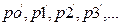 , отсекут на оси ординат системы
, отсекут на оси ординат системы  отрезки
отрезки  ,
,  ,
,  ,… пропорциональные скоростям
,… пропорциональные скоростям  в положениях 0,1,2,…,12. Полученные отрезки
в положениях 0,1,2,…,12. Полученные отрезки 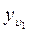 ,
,  ,
,  ,… откладываем на соответствующих ординатах диаграммы
,… откладываем на соответствующих ординатах диаграммы  (рис. 10, б), точки соединяем плавной кривой, получим диаграмму аналога скорости точки С для линейного перемещения точки С рабочего звена 3 в виде:
(рис. 10, б), точки соединяем плавной кривой, получим диаграмму аналога скорости точки С для линейного перемещения точки С рабочего звена 3 в виде:
 (м) в масштабе
(м) в масштабе  (м/мм),
(м/мм),
а для углового перемещения рабочего звена к получим аналог угловой скорости  (величина безразмерная) в масштабе
(величина безразмерная) в масштабе  (1/мм).
(1/мм).
Для построения диаграммы  или
или  графически дифференцируем кривой
графически дифференцируем кривой  или
или  соответственно. Для этого, так же как и для скоростей, выбираем систему координат
соответственно. Для этого, так же как и для скоростей, выбираем систему координат  с общей осью ординат диаграммы скорости и перемещения, на оси абсцисс влево откладываем отрезок
с общей осью ординат диаграммы скорости и перемещения, на оси абсцисс влево откладываем отрезок 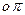 , равный
, равный  (мм) – произвольно.
(мм) – произвольно.
В точках 0', 1', 2',…, диаграммы 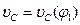 на рисунке 10, б проводим касательные, а через точку
на рисунке 10, б проводим касательные, а через точку 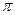 рисунка 10, в - лучи
рисунка 10, в - лучи  , параллельные проведенным касательным, которые на оси ординат системы
, параллельные проведенным касательным, которые на оси ординат системы  отсекут отрезки
отсекут отрезки  пропорциональные ускорению
пропорциональные ускорению  или
или  . Аналогичным путем строим диаграмму аналога линейного ускорения точки С
. Аналогичным путем строим диаграмму аналога линейного ускорения точки С
 (м), в масштабе
(м), в масштабе  (м/мм),
(м/мм),
или диаграмму аналога углового ускорения рабочего звена 3
 (безразмерная величина), в масштабе
(безразмерная величина), в масштабе  (1/мм).
(1/мм).
Метод графического дифференцирования не является достаточно точным, поэтому его следует применять для приближенного определения скоростей и ускорений. Для проверки правильности построения можно пользоваться известными теоремами математики, как производная функции в точке перегиба, теорема о max и min функции и т.д.
Для оценки погрешности ошибок полученных результатов кинематических параметров, необходимо произвести сравнения значении скорости и ускорения исследуемых точек в разных положениях механизма методами планов и кинематических диаграмм.  Например, формула определения погрешности ошибки скорости:
Например, формула определения погрешности ошибки скорости:


 Рисунок 10 (а, б, в)
Рисунок 10 (а, б, в)






