
* При вводе с клавиатуры символа <;> в рабочем документе отображается символ, разделяющий границы диапазона <..>.
Ниже приведен фрагмент рабочего документа Mathcad с соответствующими вычислениями.

Указание. Введите с клавиатуры ключевое слово Given (дано), затем правее и ниже ключевого слова левую часть первого уравнения системы, далее сим-вольный знак равенства (нажмите на клавиатуре клавиши <Ctrl>+<=>) и правую часть уравнения (нуль). Аналогично введите остальные два уравнения системы. Правее и ниже последнего уравнения системы введите имя функции Find (найти), перечислите в скобках имена переменных, значения которых нужно вычислить, выделите Find(x,y,z), щелкните по кнопке  в панели
в панели  . Вычисленное решение системы будет отображено после щелчка мышью вне выделяющей рамки в рабочем документе справа от стрелки в виде матрицы, каждый столбец кото-рой содержит одно из решений системы. В приведенном выше фрагменте рабочего документа найдены два решения системы: x=0,y=2,z=0 и x=l,y=3,z=l.
. Вычисленное решение системы будет отображено после щелчка мышью вне выделяющей рамки в рабочем документе справа от стрелки в виде матрицы, каждый столбец кото-рой содержит одно из решений системы. В приведенном выше фрагменте рабочего документа найдены два решения системы: x=0,y=2,z=0 и x=l,y=3,z=l.
Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.
Индивидуальные задания к работе 2
I. Упростить выражение:
| 1. | 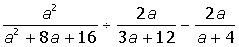
| 11. | 
| |
| 2. | 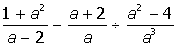
| 12. | 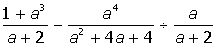
| |
| 3. | 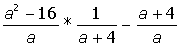
| 13. | 
| |
| 4. | 
| 14. | 
| |
| 5. | 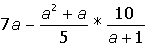
| 15. | 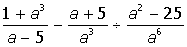
| |
| 6. | 
| 16. | 
| |
| 7. | 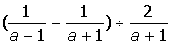
| 17. | 
| |
| 8. | 
| 18. | 
| |
| 9. | 
| 19. | 
| |
| 10. | 
| 20. | 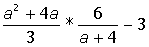
|
II. Раскрыть скобки и привести подобные в выражении:
| 1. | 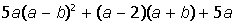
| 11. | 
| |
| 2. | 
| 12. | 
| |
| 3. | 
| 13. | 
| |
| 4. | 
| 14. | 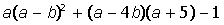
| |
| 5. | 
| 15. | 
| |
| 6. | 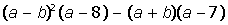
| 16. | 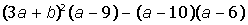
| |
| 7. | 
| 17. | 
| |
| 8. | 
| 18. | 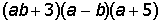
| |
| 9. | 
| 19. | 
| |
| 10. | 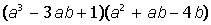
| 20. | 
|
III. Разложить на множители выражени:
| 1. | 
| 11. | 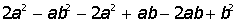
| |
| 2. | 
| 12. | 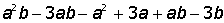
| |
| 3. | 
| 13. | 
| |
| 4. | 
| 14. | 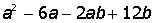
| |
| 5. | 
| 15. | 
| |
| 6. | 
| 16. | 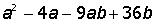
| |
| 7. | 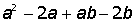
| 17. | 
| |
| 8. | 
| 18. | 
| |
| 9. | 
| 19. | 
| |
| 10. | 
| 20. | 
|
IV. Разложить на простые дроби рациональную дробь:
| 1. | 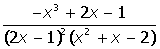
| 11. | 
| |
| 2. | 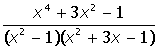
| 12. | 
| |
| 3. | 
| 13. | 
| |
| 4. | 
| 14. | 
| |
| 5. | 
| 15. | 
| |
| 6. | 
| 16. | 
| |
| 7. | 
| 17. | 
| |
| 8. | 
| 18. | 
| |
| 9. | 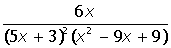
| 19. | 
| |
| 10. | 
| 20. | 
|
VII. Решить символьное уравнение:
| 1. | 
| 11. | 
| |
| 2. | 
| 12. | 
| |
| 3. | 
| 13. | 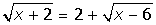
| |
| 4. | 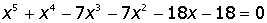
| 14. | 
| |
| 5. | 
| 15. | 
| |
| 6. | 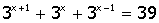
| 16. | 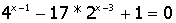
| |
| 7. | 
| 17. | 
| |
| 8. | 
| 18. | 
| |
| 9. | 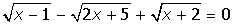
| 19. | 
| |
| 10. | 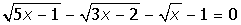
| 20. | 
|
VIII. Решить систему уравнений:
| 1. | 
| 11. | 
| |
| 2. | 
| 12. | 
| |
| 3. | 
| 13. | 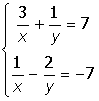
| |
| 4. | 
| 14. | 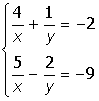
| |
| 5. | 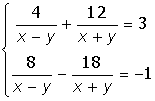
| 15. | 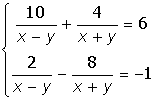
| |
| 6. | 
| 16. | 
| |
| 7. | 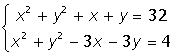
| 17. | 
| |
| 8. | 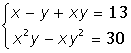
| 18. | 
| |
| 9. | 
| 19. | 
| |
| 10. | 
| 20. | 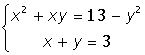
|
РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ ПО ФОРМУЛАМ КРАМЕРА
Рассмотрим решение линейных систем по формулам Крамера. Пусть

cистема n линейных алгебраических уравнений относительно n неизвестных x1, x2,..., xn.
Матрица 
называется матрицей системы, а вектор-столбец b = ( b1 b2... bn )T - столбцом правых частей системы. Рассмотренная система линейных алгебраических уравнений может быть записана в матричной форме в виде Ах = b, где х - вектор-столбец неизвестных, х = ( х1 x2... xn )T.
Справедливо следующее утверждение. Если определитель D = det A матрицы системы Ах = b отличен от нуля, то система имеет единствен-ное решение x1, х2,..., xn, определяемое формулами Крамера хi =  , где D i определитель матрицы n-го порядка, полученной из матрицы системы заменой i?го столбца столбцом правых частей.
, где D i определитель матрицы n-го порядка, полученной из матрицы системы заменой i?го столбца столбцом правых частей.
Порядок выполнения работы
Задание. Исследуйте и, если решение существует, найдите по формулам Крамера решение системы
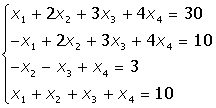

Указание:
1. Установите режим автоматических вычислений и режим отображения результатов вычислений по горизонтали.
2. Присвойте переменной ORIGIN значение, равное 1.
3. Введите матрицу и столбец правых частей.
4. Вычислите определитель матрицы.
5. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей.
Указание. Для вычисления определителей D1, D2, D3, D4 проще всего скопировать матрицу А в буфер обмена (<Ctrl>+<C> или пункт Copy меню Edit), затем вставить в помеченной позиции матрицу из буфера обмена (<Ctrl>+<V> или пункт Insert меню Edit) и затем заменить элементы соответствующего столбца элементами столбца правых частей.
6.Найдите по формулам Крамера решение системы.
Выполните индивидуальные задания приведенные ниже. Подготовьте отчет по лабораторной работе в виде экранного документа.
Индивидуальные задания к лабораторной работе 3.
Исследуйте и, если решение существует, найдите по формулам Крамера решение системы Ах = B.
1. А =  B =
B = 
2. A =  B =
B = 
3. A =  B =
B = 
4. A =  B =
B = 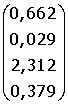
5. A =  B =
B = 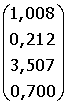
6. A =  B =
B = 
7. A =  B =
B = 
8. A =  B =
B = 
9. A =  B =
B = 
10. A =  B =
B = 
11. A = 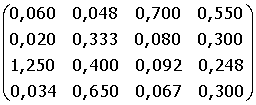 B =
B = 
12. A = 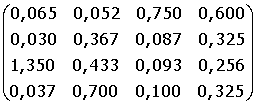 B =
B = 
13. A = 
 B =
B = 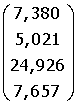
14. A =  B =
B = 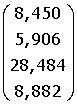
15. A =  B =
B = 
16. A =  B =
B = 
17. A =  B =
B = 
18. A = 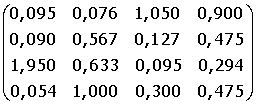 B =
B = 
1.4 Лабораторная работа 4






