9.2.1. Командное окно
После вызова MatLabиз среды Windows на экране появляется командное окно среды MatLab (рисунок 9.1.)
Это окно является основным в MatLab. В нем отображаются символы команд, которые набираются пользователем на клавиатуре, результаты выполнения этих команд, текст исполняемой программы, а также информация об ошибках выполнения программы, распознанных системой.
Признаком того, что программа MatLab готова к восприятию и выполнению очередной команды, является наличие в последней строке текстового поля знака приглашения (
), после которого стоит мигающая вертикальная черта.
В верхней части окна (под заголовком) размещена строка меню, в которой находятся меню, назначение которых общеизвестно (см., например, [10]).
9.2.2. Операции с числами
Ввод действительных чисел с клавиатуры производится по общим правилам, принятым для языков программирования высокого уровня:
- для определения дробной части мантиссы числа применяется десятичная точка;
- десятичный показатель числа записывается в виде целого числа после предварительной записи символа e;
- между записью мантиссы числа и символом e не должно быть никаких символов.
Простейшие арифметические действия:
- “+” – сложение; “-” – вычитание; “*” – умножение; “/” – деление слева направо; “\” - деление справа налево; “^” – возведение в степень.
Вывод промежуточной информации в командное окно подчинятся следующим правилам:
- если запись оператора не заканчивается символом “;”, результат действия этого оператора сразу же выводится в командное окно;
- если запись оператора заканчивается символом “;”, результат его действия не отображается в командном окне;
- если оператор не содержит знака присвоения “=”, то значение результата присваивается специальной системной переменной ans;
- полученное значение можно использовать в последующих операторах вычислений под именем ans; при этом следует помнить, что значение переменной ans изменяется после действия очередного оператора без знака присвоения;
- в общем случае форма вывода результата в командное окно имеет вид:
.
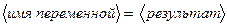В системе MatLab имеется несколько имен переменных, которые используются системой и входят в состав зарезервированных (Эти переменные можно использовать в математических выражениях):
- 
- мнимая единица (
);
- 
- число 
(сохраняется в виде 3.141592653589793);
- 
- обозначение машинной бесконечности 
;
- 
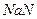- обозначение неопределенного результата (например 
);
- 
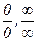- результат последней операции без знака присвоения.
Ввод значений комплексного числа.
Язык системы MatLab, в отличие от многих языков программирования высокого уровня, содержит очень простую в пользовании встроенную арифметику комплексных чисел. Большинство элементарных математических функций построено таким образом, что аргументы предполагаются комплексными числами, а результаты также формируются как комплексные числа.
Для обозначения мнимой единицы в MatLab зарезервировано два имени -i и –j. Ввод с клавиатуры значения комплексного числа производится путем записи в командном окне строки вида
9.2.3. Простейшие операции с векторами и матрицами
 |
Под вектором в MatLab понимается одномерный массив, а под матрицей – двумерный массив. По умолчанию предполагается, что любая заданная переменная является вектором или матрицей. Например, отдельно заданное число программа воспринимает как матрицу размером (1*1), а вектор-строку с N элементами – как матрицу размером (1*N).
Ввод векторов и матриц
 |
Исходные значения векторов можно задавать с клавиатуры путем поэлементного ввода. Для этого в строке следует вначале указать имя вектора, потом поставить знак присвоения “=”, далее – открывающуюся квадратную скобку, а за ней ввести заданные значения элементов вектора, отделяя их пробелами или запятыми. Завершается строка закрывающейся квадратной скобкой.
Например, ввод вектора-стоки V=[1.2 –0.3 5], задает вектор, содержащей три элемента (рисунок 9.2)
 |
Длинный вектор можно вводить частями, которые затем объединять с помощью операции объединения в строку: V=[V1 V2] (рисунок 9.3)
Вектор-столбец вводится аналогично, но значения элементов в перечне отделяются знаком “; ”.
Ввод значений элементов матрицы осуществляется в квадратных скобках по строкам. При этом элементы строки матрицы отделяются друг от друга знаком “; ” (рисунок 9.4):
9.2.4. Некоторые функции прикладной численной математики
Операции с полиномами
Полином как функция определяется выражением
.
В MatLab полином задается и хранится в виде вектора, элементами которого являются коэффициенты полинома от 
до 
Умножение полиномов сводится к построению расширенного вектора коэффициентов по заданным векторам коэффициентов полиномов-сомножителей. Данная операция называется сверткой векторов
В MatLab эту операцию осуществляет функция 
.
Аналогично, функция 
осуществляет деление полинома 
на 
.
Пример.
Система MatLab имеет функцию 
, которая вычисляет вектор, элементы которого являются корнями заданного полинома 
.
Пусть требуется найти корни полинома
Найдем корни, используя функцию :
Обратная задача – построение вектора коэффициентов полинома по заданному вектору его корней – осуществляется функцией 
Здесь 
- заданный вектор значений корней.
Пример.
Аппроксимация и интерполяция данных
Система MatLab предоставляет удобные процедуры для аппроксимации и интерполяции данных измерений.
Полиномиальная аппроксимация данных измерений, которые сформированы как некоторый вектор Y, при некоторых значениях аргумента, которые образую вектор X такой же длины, что и вектор Y, осуществляется процедурой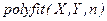 
. Здесь n порядок аппроксимирующего полинома.
Пример.
Пусть имеем массив значений аргумента
x = [1 2 3 4 5 6 7 8],
а массив соответствующих значений измеренной величины
y = [-1.1 0.2 0.5 0.8 0.7 0.6 0.4 0.1].
Тогда, применяя указанную функцию при разных значениях порядка аппроксимирующего полинома, получим:
Это значит, что заданную зависимость можно аппроксимировать кривыми различных порядков, что и демонстрируется кривыми на рисунке 9.5.
9.2.5. Построение простейших графиков
Вывод графиков в системе MatLab является настолько простой и удобной процедурой, что ею можно пользоваться даже при вычислениях в режиме калькулятора.
Основной функцией, обеспечивающей построение графиков на экране дисплея, является функция 
.
Общая форма обращения к этой процедуре такова:
.
Здесь 
- заданные векторы, элементам которых являются массивы значений аргумента 
и функции 
, соответствующих первой кривой графика; 
- массивы значений аргумента и функции второй кривой и т.д. При этом предполагается, что значения аргумента откладываются вдоль горизонтальной оси, а значения функции – вдоль вертикальной оси. Переменные являются символьными (их указание необязательно). Каждая из них может содержать три специальных символа, которые определяют тип линии, соединяющей отдельные точки графика, тип точки графика и цвет линии. Если переменные 
не указаны, то тип по умолчанию - отрезок прямой, тип точки – пиксель, а цвет устанавливается в таком порядке: синий, зеленый, красный, голубой, фиолетовый, желтый, черный и белый.
Графики в MatLab всегда выводятся в отдельном графическом окне, которое называется фигурой.
 |
По приведенной форме график изображается без сетки.
Для нанесения сетки необходимо добавить функцию 
.
Ценной особенностью графиков, построенных в MatLab, является то, что сетка координат всегда отвечает целым шагам изменения, что делает графики “читабельными”.
Пример.
Пусть требуется вывести график функции 
на промежутке от 
до 
с шагом 
.
Результат выглядит следующим образом (рисунок 9.6).
