Решение разностных уравнений методом прямой подстановки

Уравнение (8.16) записано в виде, удобном для решения методом прямой подстановки. Имея набор начальных условий (например, для i=-1, -2, …, -M) и входную последовательность по формуле (8.16)т можно непосредственно вычислить выходную последовательность для .

Пример.

Дана последовательность

Разностное уравнение имеет вид

(8.17)

с начальными условиями .

Данное уравнение можно решить подстановкой, что дает:

8.2.3.2. Решение разностных уравнений в явном виде

Хотя решение разностного уравнения подстановкой и целесообразно в некоторых случаях, значительно полезнее получить решения в явном виде.

Основная идея сводится к получению двух решений разностного уравнения: однородного и частного.

Однородное уравнение получается путем подстановки нулей вместо всех членов, содержащих элементы входной последовательности и определение отклика при нулевой входной последовательности.

Частное решение получается из подбора вида последовательности на выходе при заданной входной последовательности . Для определения произвольных постоянных однородного решения используются начальные условия.

Пример.

Решить уравнение (8.17) этим методом.

Однородное уравнение имеет вид

(8.18)

Известно, что характеристическими решениями однородных уравнений, соответствующих линейным разностным уравнениям с постоянными коэффициентами, является решение вида . Поэтому, подставляя вместо в (8.18), получим

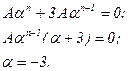
Отсюда однородное решение имеет вид

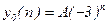. (8.19)

Частное решение, соответствующее входной последовательности , попробуем найти в виде

. (8.20)

Из уравнения (8.16) получаем

Поскольку коэффициенты при равных степенях в левой и правой частях уравнения должны совпадать, то из получаемой системы (трех уравнений) находим три искомых коэффициента: .

Таким образом, общее решение имеет вид:

, (8.21)

В этом выражении коэффициент находится из начального условия .

Тогда из (8.21) получим

(8.22)

Проверка решения (8.22) при показывает полное совпадение с приведенным выше прямым решением.

Преимущество решения (8.22) заключается в том, что оно позволяет весьма просто определить для любого конкретного .

8.2.3.3. Схемы реализации цифровых систем

Важное значение разностных уравнений состоит в том, что они непосредственно определяют способ построения цифровой системы.

Так, разностное уравнение первого порядка самого общего вида

(8.23)

можно реализовать с помощью схемы

Блок “задержки” осуществляет задержку сигнала на один отсчет.

Разностное уравнение второго порядка самого общего вида

(8.24)

может быть реализовано при помощи схемы, приведенной на рисунке 8.4.

Системы первого и второго порядка могут быть использованы при реализации систем более высокого поряджка, т.к. последние могут быть представлены в виде последовательного или параллельного соединения систем первого и второго порядка.

8.2.4. Z – преобразование

Одним из методов представления последовательностей является Z-преобразование.

Для последовательности , заданной при всех , Z-преобразование определяется следующим степенным рядом

. (8.25)

где - комплексная переменная.

8.2.4. 1. Последовательности конечной длины

Если отлична от нуля только в интервале , где - конечны, то сходится в - плоскости везде, за исключением, может быть, точк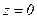и или .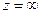

Линейную систему с постоянными параметрами, импульсная характеристика которой является последовательностью конечной длины, называют системой с конечной импульсной характеристикой, или, что то же самое, КИХ-фильтром.

Типичная импульсная характеристика конечной длины изображена на рисунке 8.5.

Системой (фильтром) с бесконечной импульсной характеристикой (БИХ) называется система (фильтр), длина импульсной характеристики которой не ограничена слева или справа или с обеих сторон.

8.2.4. 2. Примеры Z-преобразования.

1. Найти Z -преобразование единичного импульса.

Решение.

Так как 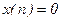при любых , кроме , при котором , то согласно (8.25) имеем

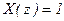. (8.26)

2. Найти Z -преобразование единичного скачка.

Так как 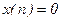везде, кроме , где , то из (8.25) получим

. (8.27)

Бесконечный ряд сходится при , т.к. имеет единственную особую точку .

(Примечание. Результат (8.27) вытекает из формулы суммы геометрической прогрессии

3. Найти Z -преобразование комплексной экспоненты.

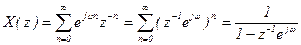. (8.28)

сходится при , т.к. единственной особой точкой является .

4. Найти Z -преобразование простой экспоненциальной последовательности.

В этом случае 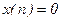при и при .

Тогда согласно (8.25) получаем

. (8.29)

сходится при , т.к. единственной особой точкой является .

8.2.4. 3. Свойства Z – преобразования

Линейность.

Z – преобразование линейно.

Пусть - z – преобразования последовательностей .

Тогда справедливо

. (8.30)

Задержка.

Если ,

то

. (8.31)

Это свойство полезно при переходе от представления линейной системы с постоянными переменными к представлению ее z – преобразованием и наоборот.

Пример.

Пусть имеется разностное уравнение

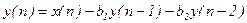Представим его в виде z – преобразования

или

где

Свертка последовательностей

Пусть входные и выходные последовательности дискретной линейной системы с постоянными параметрами, - импульсная характеристика системы, - их соответствующие z – преобразования.