Теория дискретных линейных систем связана с описанием и обработкой временных и частотных последовательностей.
Будем рассматривать частный случай, как наиболее распространенный, когда квантование элементов последовательности по уровню отсутствует (при общей теории дискретных систем, где квантование производится как по времени, так и по уровню).
8.2.1. Последовательности
Дискретный сигнал определяется лишь для дискретных значений независимой переменной – времени t.
Обычно время квантуется равномерно, т.е.
, (8.1)
где 
- интервал между отсчетами.
Математически дискретные сигналы представляются в виде непрерывной последовательности чисел.
Для описания может быть использовано одно из следующих обозначений:
; 
(8.2)
; (8.3)
; (8.4)
; (8.5)
Способы обозначения (8.2) и (8.4) используются при неравномерном расположении отсчетов, а (8.3) и (8.5) – при равномерном.
Примеры важных последовательностей.
1. Цифровой единичный импульс - основная последовательность 
(8.6)
Этот импульс аналогичен единичному импульсу 
в аналоговых системах.
Отличие между ними:
- физически реализуемый сигнал;
- обобщенная функция (или распределение).
2. Единичный импульс, задержанный на 
отсчетов 
:
(8.7)
3. Единичный скачок 
:
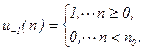(8.8)
Существует связь между единичным скачком и единичным импульсом:
. (8.9)
4. Экспонента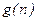 
:
(8.10)
5. Косинусоида :
. (8.11)
Произвольные последовательности легко выражаются через основные последовательности (единичный импульс, используя задержку и масштабирование):
если
,
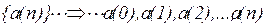то эту последовательность, используя (8.7), можно представить
. (8.12)
8.2.2. Линейные системы с постоянными параметрами
Дискретная система по существу является алгоритмом преобразования одной последовательности (входной) в другую (выходную)
,
где 
- оператор, его вид зависит от свойств конкретной системы.
 |
Соответствующая схема может быть представлена в виде, приведенном на рисунке 8.1.
8.2.2.1. Определение линейной системы
Если 
, 
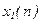- входные последовательности, 
, 
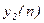- выходные последовательности, и 
- константы, то в линейной системе имеет место
. (8.13)
8.2.2.2. Определение системы с постоянными параметрами
Если 
- входная последовательность и 
- соответствующая выходная последовательность, то входной последовательности 
при любых соответствует на выходе последовательность 
.
В линейной системе с постоянными параметрами входная и выходная последовательности связаны соотношением типа свертки.
Пусть
- входная последовательность;
- соответствующая выходная последовательность;
- отклик системы на единичный импульс (импульсная характеристика системы).
Используя (8.12), можно последовательность представить
.
Поскольку - отклик системы на последовательность 
, а
параметры системы постоянны, то 
- есть отклик на последовательность 
.
Из свойств линейности следует, что откликом на последовательность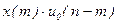 
должна быть последовательность 
. Поэтому отклик на будет
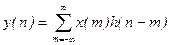. (8.14)
Он имеет вид свертки, что и доказать.
Простой заменой переменных выражение (8.14) может быть преобразовано к виду
 |
. (8.15)
Это может быть отражено схемой
8.2.3. Разностные уравнения
В общем случае линейное разностное уравнение порядка M с постоянными коэффициентами имеет вид
, (8.16)
где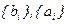 
описывают конкретную систему, причем 
.
