В теле, определяемой функции, могут использоваться глобальные и локальные переменные. Например, в теле следующих функций
In[4]:= exprod[n_]:= Expand[Product[x+i, {i, 1, n}]]
In[5]:= cex[n_, i_]:= (t = exprod[n]; Coefficient[t, x^i])
переменные x и t будут глобальными. Значения глобальных переменных доступны для любых выражений в среде Mathematica.
In[6]:= exprod[5]
Out[6]= 120 + 274 x + 225 x2 + 85 x3 + 15 x4 + x5
In[7]:= cex[5, 3]
Out[7]= 85
In[8]:= t t - глобальная переменная
Out[8]= 120 + 274 x + 225 x2 + 85 x3 + 15 x4 + x5
In[9]:= x=a; x - глобальная переменная
In[10]:= exprond[3]
Out[10]= 6 + 11 a + 6 a2 + a3
Локальные переменные в теле функции или процедуры вводятся с помощью специальной функции
Module[{a,b,c,...}, procedure],
в которой a, b, c,... локальные переменные. Определим функцию ncex с использованием локальной переменной u.
In[11]:= ncex[n_, i_]:= Module[{u}, u = exprod[n]; Coefficient[u, x^i]] u - локальная переменная
In[12]:= ncex[5, 3]
Out[12]= 85
In[13]:= u
Out[13]= u
Структурные операторы
Язык программной системы Mathematica является функциональным языком, поэтому структурные операторы определяются как функции возвращающие соответствующие значенрия.
Goto[tag] - безусловный переход к метке tag.
Label[tag] - определяет метку tag.
If[conditioon, t, f] - условный оператор If возвращает значение t, если condition=true и возвращает значение f, если condition=false.
Do[expr, {i, imax}] - цикл с индексом Do вычисляет expr imax - раз. При этом i меняется от1 до imax с шагом 1.
Do[expr, {i, imin, imax, di] - определяет цикл с индексом i, изменяющимся от imin до imax с шагом di.
Table[expr, {i, imax}] - создает список (list) значений, вычисляемых в expr. Число элементов списка равно imax.
Table[expr, {i, imax},{j, jmax]] - создает матрицу, которая содержит imax строк и jmax столбцов.
While[condition, body] - цикл с предусловием.
Рекурсивный вызов функций
При определении функций в программной системе Mathematica широко используется рекурсия, так как многие математические объекты определяются с помощью рекурсивных выражений. Простейшим примером является факториал:
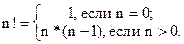
In[1]:= Factorial[n_]:= If[n==0, 1, n*Factorial[n-1]]
In[2]:= Factorial[4]
Out[2]= 24
Пакеты функций
Приведенные выше определения функций в интерактивном режиме работы программной систем размещаются в оперативной памяти. По окончанию работы с программной системой данные определения функций уничтожаются. Пользователь может создавать собственные функции и объединять их в пакеты функций. Пакет функций (Package) представляет собой текстовый файл в кодах ASCII с расширением m. Файлы пакетов функций хранятся в подкаталогах каталога PACKAGES система Mathematica.
При создании пакета функций используются следующие средства:
BeginPackage["NonLSys`AffinS`"] - определяет начало пакета и текущий контекст пакета NonLSys`AffinS`, который является маршрутом доступа к файлу AffinS.m.
f::usage="Text" - вводит объект для экспорта и декларирует функцию f, которая описывается в теле пакета. Каждая функция пользователя, включаемая в пакет должна декларироваться. "Text" представляет собой комментарий, который описывает назначение функции f. При выполнении команды?<имя функции> выводится комментарий "Text"
Begin["`Private`"] - устанавливает текущий контекст для внутреннего использования в пакете. Фактически открывает тело пакета.
f[arg]:= <тело функции> - определение функций включенной в пакет.
End[ ] - возврат к предыдущему контексту.
EndPackage[ ] - конец пакета.
ПРИМЕР определения пакета.
BeginPackage["NonLSys`AffinS2`"]
(* Здесь должен располагаться комментарий *)
GradF::usage="GradF[h, x] returns the gradient dh={dh/dx1...
dh/dxn} of function h. x={x1... xn} is array of state space
variables."
Jacobi::usage="Jacoby[f, x] returns the Jacobi matrix J=df/dx
of vector f. f={{f1(x)},{f2(x)},...} is vector colums"
Begin["`Private`"]
GradF[hh_, xx_]:=Module[{i}, Table[D[hh, xx[[i]] ], {i, Length[xx]}]]
Jacobi[ff_, xx_]:= Module[{i, j},
Table[D[ff[[i, 1]], xx[[j]]], {i, Length[ff]}, {j, Length[xx]}]]
End[ ]
EndPackage[ ] (* NonLSys`AffinS2` *)
После запуска программной системы загружаются лишь встроенные функции ядра. Загрузка функций пакета осуществляется следующим образом.
In[1]:= <<NonLSys`AffinS2`
Построение графиков
Mathematica предоставляет набор функций для построения графиков функций, зависящих от одой и двух переменных, при этом аргументы функции могут быть заданы параметрически. Кроме того графики можно строить в различных системах координат (линейных, логарифмических, полярных и т.д.).
Двухмерные графики
Построение графика функции от одной переменной
Plot[f[x], {x, xmin, xmax}],
где f[x] – функция одной переменной, x – аргумент функции, xmin – начальное значение x, xmax – конечное значение x.
In[1]:= Plot[Sin[x], {x, 0, 2*Pi}]
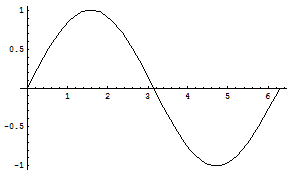
Out[1] = Graphics
При построении графика можно задавать опции, позволяющие нарисовать рамку Frame, наложить сетку GridLines, дать наименования осям GridLines.
In[2]:= Plot[Sin[x^2], {x, 0, 3}, Frame -> True, GridLines -> Automatic,
AxesLabel -> {"x", "Sin[x]"}]
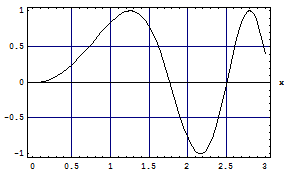
Out[2] = Graphics
Опция PlotRange позволяет задать границы по вертикальной оси при отображении графика.
In[3]:= Plot[Sin[x^2], {x, 0, 3}, PlotRange -> {0, 1.2}]
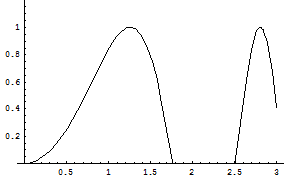
Out[3] = Graphics
Функция Show позволяет вывести вместе несколько графиков, построенных ранее.
In[4]:= Show[Out[2], Out[3]]
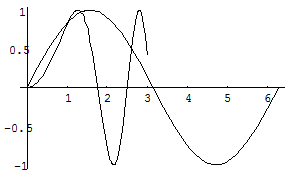
Out[4] = Graphics






