Решение алгебраических уравнений в аналитическом виде:
Solve[lhs == rhs, x] - решить уравнение lhs == rhs относительно переменной x.
Solve 
- решить систему уравнений относительно переменных 
.
Численное решение алгебраических уравнений:
NSolve 
- численная аппроксимация корней полиномиального уравнения.
FindRoot 
- находит решение уравнения численным методом, стартуя из точки 
.
Дифференциальные уравнения
a) DSolve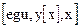 
- находит решение дифференциального уравнения 
, как функцию y[x] от независимой переменной x.
ПРИМЕР аналитического решения дифференциального уравнения.
In[1]= DSolve[y'[x]==2 a x, y[x], x]
Out[1]= {{y[x]->a x2+c[1]}}
b) NDSolve 
- численное решение дифференциальных уравнений на промежутке 
.
ПРИМЕР решения системы дифференциальных уравнений численным методом.
Пусть необходимо решить систему дифференциальных уравнений 2-го порядка
с начальными условиями
относительно переменных 
на промежутке времени t от 0 до 20 секунд.
In[1]:= NDSolve[{x1'[t] == x2[t],
x2'[t] == x2[t] * (1 - x1[t]^2) - x1[t],
x1[0] == 3.0,x2[0] == 0,5},
{x1[t], x2[t]}, {t, 0,20}]
Out[1]= {{x1[t] -> InterpolatingFunction[{0., 20.}, <>][t],
x2[t] -> InterpolatingFunction[{0., 20.}, <>][t]}}
Решение системы дифференциальных уравнений найдено в виде интерполяционной функции {{x1[t] -> InterpolatingFunction[{0., 20.}, <>][t],
x2[t] -> InterpolatingFunction[{0., 20.}, <>][t]}}
Графический вывод фазовых кривых:
In[2]:= ParametricPlot[Evaluate[{x1[t], x2[t]} /.%], {t, 0, 20}]
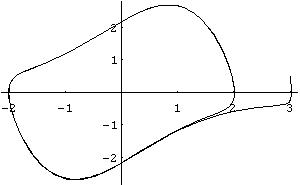
Out[2]= -Graphics-
Графический вывод временных процессов:
In[3]:= Plot[Evaluate[{x1[t], x2[t]} /.%%], {t, 0, 20}]
Out[3]= -Graphics-
Правила преобразования
Правила преобразования применяются для формальной подстановки в математических выражениях вместо lhs компоненты rhs компоненты. Синтаксис записи правил преобразования имеет следующий вид:
expr /.lhs -> rhs,
где expr - математическое выражение; lhs - компонент, который необходимо заменить; rhs - компонент, на который заменяется lhs; -> - оператор замены.
Если к выражению необходимо применить несколько правил преобразования, то правила необходимо записать в виде списка:
expr /. {lhs1 -> rhs1, lhs2 ->rhs2...}
ПРИМЕРЫ применения правил преобразования
In[1]:= x + y /. x->3 - вместо x в выражение подставляется 3
Out[1]= 3 + y
In[2]:= x + y /. {x->a, y->b} - вместо x в выражение подставляется a, а вместо y подстав-
Out[2]= a + b ляется b
expr /.{rules, rules,...} - дает список результатов после применения каждого правила
In[3]:= x+y /. {{x->1, y->2}, {x->4, y->2}}
Out[3]= {3, 6}
expr//.rules - правила преобразования применяются друг к другу и к выражению expr
In[4]:= x^2 + y^6 /. { x->2+a } - обычное применение правил
Out[4]= (2 + a)2 + y6
In[5]:= x^2+y^6 //. { x->2+a, a->3 } - применение правил друг к другу и к выражению
Out[5] = 25 + y6
Замечание: Правило преобразования можно связать с именем.
In[6]:= rt = Sin[x_]^2 + Cos[x]^2 -> 1;
In[7]:= x - Cos[a x^2 + b x + c]^2 - Sin[a x^2 + b x + c]^2 /. rt
Out[7]= x - 1
Функции и программы
Определение функции
Функции в языке программной системы Mathematica определяются следующим образом:
<имя функции>[<список формальных параметров>]:=<тело функции>.
После каждого имени параметра в списке формальных параметров ставится символ "_". Символ "_" в конце имени параметра означат, что параметр является формальным. В теле функции за именем формальный переменой символ подчеркивания не ставится. Пользователь всегда может вывести определение функции. Для этого необходимо ввести команду
?<имя функции>.
Определение функции в процессе работы можно удалить с помощью команды Clear[<имя функции>].
ПРИМЕРЫ:
In[1]:= f[x_]:= x^2 - определение функции
In[2]:= f[a+1] - вызов функции
Out[2]:=( 1 + a)2
In[3]:= ?f - вывод определения функции
Global `f
f[x_]:=x^2
