1 Вынужденные колебания
2 Параметры вынужденных колебаний
3 Явление резонанса
Основные понятия по теме
Рассмотрим электрическую цепь, содержащую активное сопротивление R, конденсатор С, катушку индуктивности L и источник переменного напряжения U (рисунок 11.1).
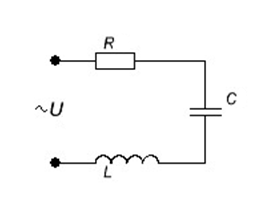
Рисунок 11.1 – Электрическая цепь, содержащая R, С, L
и источник переменного напряжения
В соответствии со вторым законом Кирхгофа полная Э.Д.С., действующая в цепи, равна сумме падений напряжения на всех участках цепи
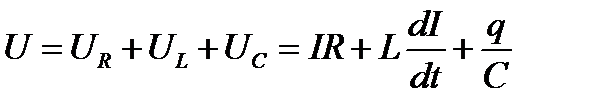(11.1)
Здесь 
- напряжение на катушке, равное с обратным знаком Э.Д.С. самоиндукции, возникающей в катушке, 
– падение напряжения на активном сопротивлении, 
- разность потенциалов обкладок конденсатора. Дифференцируя уравнение (11.1) по времени и учитывая, что dq/dt = I, получим:
(11.2)
Наибольший интерес представляет анализ гармонического переменного тока, поскольку с помощью преобразования Фурье произвольный ток может быть представлен в виде совокупности гармонических составляющих. Для удобства дифференцирования силу тока и напряжение в цепи представим в комплексной форме
, 
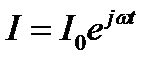, (11.3)
где I0 и U0 - некоторые комплексные числа. При этом необходимо иметь ввиду, что ток и напряжение, как реальные физические величины, должны описываться действительной частью выражений (11.3). Поэтому, после выполнения преобразований согласно (11.2), в найденных решениях необходимо выделить действительную часть. Поскольку уравнение (11.2) является линейным, то окончательный результат будет таким же, как и в случае выполнения преобразования только над действительной частью выражений (11.3). Подставляя (11.3) в уравнение (11.2), после дифференцирования получаем:
(11.4)
Разделив обе части уравнения на 
, можно записать (11.4) в виде
, (11.5)
выражающем закон Ома для цепи переменного тока. Комплексная величина
(11.6)
называется импедансом, она играет роль сопротивления цепи, зависящего от частоты тока w. Импеданс характеризует соотношение между амплитудами и фазами тока и напряжения в цепи, содержащей активное сопротивление, емкость и индуктивность.
Зависимость между током и напряжением (11.5) можно проиллюстрировать графически, путем представления комплексных величин векторами на комплексной плоскости. При этом гармонически изменяющаяся величина изображается вектором, вращающимся с частотой w вокруг начала координат против часовой стрелки. Длина вектора равна амплитуде колебаний рассматриваемой физической величины, а угол между вектором и осью ОХ равен фазе колебаний. Совместим ось ОX с вектором силы тока I в произвольный момент времени (рисунок 11.2), тогда вектор падения напряжения на активном сопротивлении Uа = IR также будет направлен вдоль оси ОХ. Падение напряжения на катушке и конденсаторе соответственно равно
, (11.7)
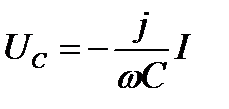. (11.8)
При определении ориентации векторов UL и UC необходимо учесть, что, согласно формуле Эйлера, 
. Следовательно, умножение произвольной комплексной величины 
на 
эквивалентно повороту вектора на комплексной плоскости на угол 
без изменения длины этого вектора:
. (11.9)
В соответствии с этим правилом, напряжение на катушке (формула 11.7) всегда опережает по фазе силу тока на 
, а напряжение на конденсаторе (формула 11.8) отстает по фазе от силы тока на 
. Построив на комплексной плоскости векторы UL и Uc, можно графически определить полное напряжение как сумму падений напряжения на всех участках цепи.
|
|
|
|
|
|
|
Рисунок 11.2 – Векторная диаграмма цепи R, С, L, если индуктивное сопротивление 
больше емкостного 
Векторная диаграмма цепи (рисунок 11.2) показывает, что полное напряжение U может как опережать по фазе силу тока, так и отставать от нее. При этом сдвиг фаз между током и напряжением в цепи определяется выражением
, (11.10)
а амплитуда напряжения и силы тока связаны соотношением:
. (11.11)
Формула (11.10) показывает, что сдвиг фаз между током и напряжением может принимать как положительные, так и отрицательные значения в зависимости от соотношения параметров цепи и частоты тока. Для частоты тока 
, совпадающей с собственной частотой колебательного контура, сдвиг фаз j равен нулю. В этом случае напряжение на конденсаторе и катушке взаимно компенсируются (они равны по величине, но противоположны по знаку, поскольку имеют относительно друг друга сдвиг фаз, равный p). Сила тока такая же, как при отсутствии в цепи реактивных элементов, то есть принимает максимальное значение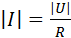 
(в последовательной цепи имеет место резонанс напряжений).
Сдвиг фаз между током и напряжением в цепи переменного тока можно определить с помощью электронного осциллографа. Допустим, необходимо измерить сдвиг фаз между двумя гармоническими сигналами одинаковой частоты. Подадим эти сигналы на горизонтально и вертикально отклоняющие пластины осциллографа. Тогда смещения электронного луча по горизонтали и вертикали будут изменяться с течением времени следующим образом:
, 
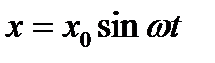, (11.12)
здесь w - частота колебания, j - искомый сдвиг фаз, x0 и y0 - максимальные отклонения электронного луча, зависящие от амплитуды исследуемых сигналов и коэффициентов усиления соответствующих каналов осциллографа. Исключая время t, в результате тригонометрических преобразований из (11.12) можно получить уравнение эллипса, описываемого электронным лучом на экране осциллографа:
, (11.13)
Ориентация этого эллипса относительно осей ОХ и ОY зависит как от сдвига фаз j, так и от максимальных смещений луча x0, y0. Перейдем к системе координат Х′ОY′, оси которой повернуты на угол p/4 относительно осей ХОY. В соответствии с правилом преобразования координат при повороте на угол a, получаем
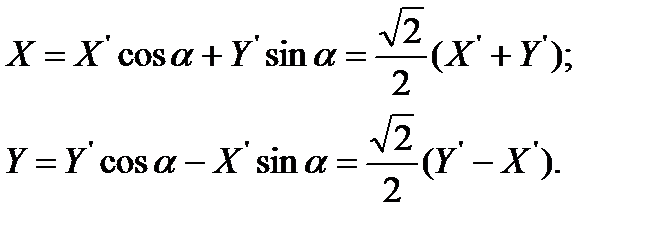
В случае равенства амплитуд x0 = y0, выполнения которого можно добиться регулировкой коэффициентов усиления каналов осциллографа, уравнение эллипса в повернутой системе координат запишется в канонической форме
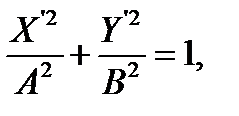
где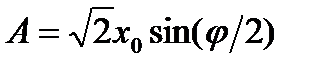 
, 
- главные полуоси эллипса (рисунок 11.3). Измерив непосредственно на экране осциллографа длину больших полуосей, можно определить сдвиг фаз исследуемых колебаний.
Рисунок 11.3 – Определение сдвига фаз
с помощью осциллограммы
Вопросы для самоконтроля
1 Проведите аналогию между вынужденными колебаниями механических и электрических колебательных систем. Сделайте вывод о характере колебаний в этих системах, о влиянии параметров систем на явление резонанса.
2 Охарактеризуйте режим резонанса в контуре.
3 Начертите вид зависимостей XL = f(w), XC = f(w), I = f(w).
4 Выберите R, L, C так, чтобы обеспечить f0 = 5 кГц (резонансная частота), Q = 50 (добротность).
5 Постройте векторные диаграммы контура до резонанса, после резонанса.
Лабораторная работа 11
