Предположим, что площадь сечения тела плоскостью, перпендикулярной оси ОХ, может быть выражена функцией от х: 
при 
, тогда объем тела, заключенный между перпендикулярными оси ОХ плоскостями 
и 
, находится по формуле
. (4.10)
Если криволинейную трапецию (рис.4.10) вращать вокруг оси ОХ, то объем тела вращения будет равен
. (4.11)
Если плоская область, ограниченная кривыми 
и прямыми и , вращается вокруг оси ОХ, то
(4.12)
Аналогично можно записать формулы для вычисления объемов тел вращения вокруг оси ОY:
(4.13)
(4.14)
Если кривые, ограничивающие плоскую область заданы в параметрическом виде, то к формулам (4.10 - 4.14) следует применить соответствующие замены переменной.
Если криволинейный сектор вращать вокруг полярной оси (см.рис.5.7), то
. (4.15)
Пример 49. Вычислить объем тела, полученного при вращении дуги кривой 
, 
вокруг оси ОХ.
Решение. Данная кривая 
называется цепной линией. График ее изображен на рис.4.9. Объем тела вращения (рис.4.10) вычислим по формуле (4.11)
.
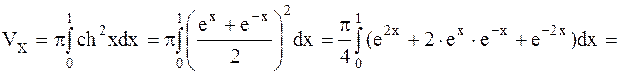
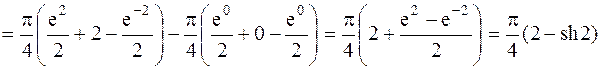Пример 50. Найти объем параболоида вращения, радиус основания которого равен R, а высота - Н.
Решение. Искомый параболоид вращения с указанными параметрами получится, если будем вращать вокруг оси ОY параболу 
, 
(рис.4.11; 4.12), где параметр k легко вычислить исходя из данного условия.
Если 
, то 
, поэтому
.
Далее воспользуемся формулой (4.13)
.
Если 
то 
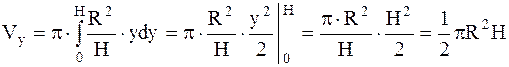(ед3).
Пример 51. Найти объем тела вращения кривой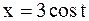 
, 
вокруг оси ОХ.
Решение. Данная кривая задана в параметрическом виде -
это эллипс (рис.4.13). Искомой фигурой вращения
является эллипсоид. Найдем 
по формуле (4.11)
Если 
, то 
, 
.
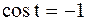Если 
, то 
, 
.
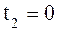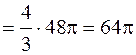(куб.ед.).
Вычисление площади поверхностей тел вращения
Площадь поверхности, образованной вращением гладкой кривой АВ вокруг оси ОХ, равна
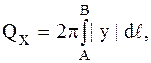где 
- дифференциал дуги кривой.
В зависимости от задания кривой - явное, в параметрическом виде или в полярных координатах - указанную формулу можно расписать так
. (4.16)
. (4.17)
. (4.18)
Пример 52. Найти площадь поверхности, образованной вращением вокруг оси ОХ дуги кривой 
, .
Решение. или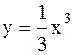 
Воспользуемся формулой (4.16)
С помощью определенного интеграла можно вычислить и многие другие геометрические и физические характеристики фигур: статические моменты и моменты инерции плоских фигур, координаты центра тяжести дуг кривых и плоских фигур, работу, давление и пр. Подробнее об этом см. [2], Гл.XII, [2] §§6,7,8,9.
Список рекомендуемой литературы
1. Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальное и интегральное исчисления. - М.: Наука, 1980. 464.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления. ТТ.1- 2, М.: Интеграл-Пресс, 2001,2002. - 416с., 544с.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. ЧЧ. 1-2. - М.: Высшая школа, 1980-2000. - 304с., 416с.
4. Запорожец Г.И. Руководство к решению задач по математическому анализу. - М.: Высшая школа, 1966. - 460с.
