а) Необходимо вычислить интеграл  ,
,
где f(x) непрерывная функция на [a,b].
Перейдем к новой переменной t, полагая  . Пусть
. Пусть  , кроме того, при изменении t от a до b значения функции
, кроме того, при изменении t от a до b значения функции  не выходят за пределы сегмента [a,b]. Предположим, что функция
не выходят за пределы сегмента [a,b]. Предположим, что функция  непрерывно дифференцируема на промежутке [a,b], то справедлива следующая формула замены переменной
непрерывно дифференцируема на промежутке [a,b], то справедлива следующая формула замены переменной
 .
.
Пример 35. Вычислить 
Решение. Преобразуем подкоренное выражение, выделив полный квадрат
 .
.
Введем новую переменную:  тогда
тогда  ,
,
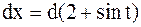 или
или 
Найдем пределы интегрирования новой переменной t:
если  , то
, то 
если  , то
, то  .
.
Воспользуемся формулой замены переменной в определенном интеграле, получим
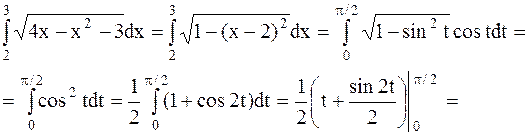

Заметим, что в данном случае при применении формулы замены переменной отпадает необходимость возвращения к старой переменной х по сравнению с неопределенным интегралом. Это вполне объяснимо, ибо определенный интеграл есть некоторое постоянное число, в то время как неопределенный интеграл от той же самой функции есть некоторая функция.
б) Часто вместо замены переменной  употребляют обратную замену переменной
употребляют обратную замену переменной  . На конкретном примере покажем, как это делается.
. На конкретном примере покажем, как это делается.
Покажем это на конкретном примере.
Пример 36. Вычислить  .
.
Решение. Пусть  , тогда
, тогда 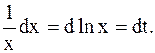
Если  то
то  если
если  , то
, то 
Следовательно,

Формула интегрирования по частям в определенном интеграле
Пусть  и
и  - непрерывные функции вместе со своими первыми производными на [a,b], тогда справедлива формула интегрирования по частям:
- непрерывные функции вместе со своими первыми производными на [a,b], тогда справедлива формула интегрирования по частям:

Пример 37. Вычислить интеграл  .
.
Решение. Применим полученную формулу

Подробнее о методах интегрирования в определенном интеграле см.[1] с.399-403.
Несобственные интегралы
Определение определенного интеграла, его свойства и методы интегрирования рассматривались в предположении, что промежуток интегрирования [a,b] конечен и функция f(x) непрерывна на нем.
Иногда приходится отказываться от одного или обоих этих предположений. В этом случае мы приходим к понятию несобственного интеграла.
Несобственные интегралы с бесконечными
Пределами интегрирования
Рассмотрим функцию  , непрерывную на бесконечном промежутке
, непрерывную на бесконечном промежутке  .
.
Несобственным интегралом от функции f(x) по промежутку  называется
называется  :
:
 .
.
Если указанный предел существует и конечен, то несобственный интеграл с бесконечным пределом интегрирования называется сходящимся, в противном случае - расходящимся.
Если  на
на  и
и  , то данный интеграл представляет собой площадь бесконечной криволинейной трапеции, ограниченной кривой
, то данный интеграл представляет собой площадь бесконечной криволинейной трапеции, ограниченной кривой  , прямой
, прямой  и бесконечным интервалом
и бесконечным интервалом  .
.
 |
Аналогично определяется несобственный интеграл на промежутке  :
:

а на интервале 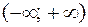 определяется формулой
определяется формулой

где с - любое действительное число.
Если сравнить две криволинейные трапеции на рис.3.1, то конечность или бесконечность их соответствующих несобственных интегралов зависит от скорости убывания функции  и
и  при
при  .
.
Так, например,  сходится при
сходится при 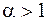 и расходится при
и расходится при  .
.
В этом легко убедится, вычислив  , если
, если  .
.
Если  , то
, то 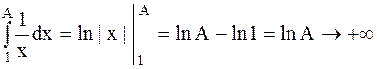 при
при  , поэтому
, поэтому  - расходится, следовательно, и площадь соответствующей криволинейной трапеции бесконечна.
- расходится, следовательно, и площадь соответствующей криволинейной трапеции бесконечна.

 - несобственный интеграл сходящийся, следовательно, площадь криволинейной трапеции, ограниченной линиями
- несобственный интеграл сходящийся, следовательно, площадь криволинейной трапеции, ограниченной линиями  и бесконечным промежутком
и бесконечным промежутком  , является конечной и равна 1.
, является конечной и равна 1.
Пример 38. Исследовать на сходимость несобственный интеграл  .
.
Решение. Воспользуемся определением несобственного интеграла с бесконечным нижним пределом интегрирования и далее - формулой интегрирования по частям

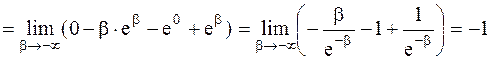 .
.
Несобственный интеграл сходится.
Пример 39. Вычислить несобственный интеграл или установить его расходимость  .
.
Решение. Воспользуемся определением несобственного интеграла с бесконечными пределами интегрирования. Полагаем  .
.



Признак сравнения. Пусть в промежутке  функции f(x) и g(x) непрерывны и
функции f(x) и g(x) непрерывны и  . Если
. Если  сходится, то сходится и интеграл
сходится, то сходится и интеграл  . Если интеграл
. Если интеграл  расходится, то и
расходится, то и  также расходится.
также расходится.
Замечание. Аналогичное утверждение верно для несобственных интегралов и по другим бесконечным пределам интегрирования.
Пример 40. Исследовать на сходимость несобственный интеграл  .
.
Решение. Проведем сравнительный анализ подынтегральной функции при  .
.

 .
.
Но  сходится, т.к.
сходится, т.к.  (см. рассуждения выше). Следовательно, по признаку сравнения сходится и данный интеграл.
(см. рассуждения выше). Следовательно, по признаку сравнения сходится и данный интеграл.




