Пусть функция  имеет разрыв II рода на [a,b] либо в точках а и b, либо в точке
имеет разрыв II рода на [a,b] либо в точках а и b, либо в точке  , тогда несобственные интегралы от разрывной функции определяются следующим образом:
, тогда несобственные интегралы от разрывной функции определяются следующим образом:
1)  - точка разрыва, то
- точка разрыва, то
 ;
;
2)  - точка разрыва, то
- точка разрыва, то
 ,
,
3) 
 , с - точка разрыва, то
, с - точка разрыва, то

Если указанные пределы существуют и конечны, то несобственные интегралы называются сходящимися, в противном случае расходящимися.
Признак сравнения. Пусть функции f(x) и g(x) в промежутках [a,b) непрерывны, а в точке  имеют разрыв II рода; кроме того
имеют разрыв II рода; кроме того  . Если
. Если 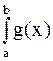 сходится, то сходится
сходится, то сходится  .
.
Если  расходится, то расходится
расходится, то расходится  .
.
Пример 41. Исследовать на сходимость несобственный интеграл  .
.
Решение. Функция  в точке
в точке  имеет разрыв II рода, поэтому
имеет разрыв II рода, поэтому
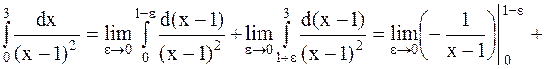
 .
.
Интеграл расходящийся.
Пример 42. Исследовать на сходимость несобственный интеграл от неограниченной функции
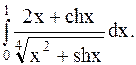
Решение. При  знаменатель функции обращается в 0, а числитель равен 1, следовательно,
знаменатель функции обращается в 0, а числитель равен 1, следовательно,  - точка разрыва II рода. Во всех остальных точках промежутка (0;1] подынтегральная функция непрерывна.
- точка разрыва II рода. Во всех остальных точках промежутка (0;1] подынтегральная функция непрерывна.
Заметим также, что 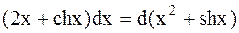 ,
,

Используя определение несобственного интеграла от неограниченной функции, а также формулу Ньютона-Лейбница получим

Интеграл сходящийся.
Приложения определенного интеграла
Вычисление площади плоской фигуры в
Декартовых координатах
Если задана непрерывная функция  на [a,b],
на [a,b],  , то определенный интеграл с геометрической точки зрения представляет собой площадь так называемой, криволинейной трапеции (рис.4.1).
, то определенный интеграл с геометрической точки зрения представляет собой площадь так называемой, криволинейной трапеции (рис.4.1).
 | |||
| |||
(4.1)
Пусть криволинейная трапеция с основанием [a,b] ограничена снизу кривой  (рис.4.2), то из соображений симметрии видим, что
(рис.4.2), то из соображений симметрии видим, что
 | |||
| |||
(4.2)
В некоторых случаях, чтобы вычислить площадь искомой фигуры, необходимо разбить ее на сумму или разность двух или более криволинейных трапеций и применить формулы (4.1) или (4.2) (рис.4.3. и 4.4)


Пример 43. Вычислить площадь фигуры, ограниченной линиями 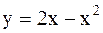 и
и  .
.
Решение.  - парабола. Найдем ее вершину и точки пересечения с осями координат.
- парабола. Найдем ее вершину и точки пересечения с осями координат.
 ;
; 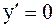 или
или  ,
, 
Если  , то
, то 
 - вершина параболы.
- вершина параболы.
 или
или  или
или 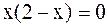
 .
.
 - прямая линия.
- прямая линия.
Найдем абсциссы точек пересечения прямой и параболы:
 или
или 
 .
.
Для вычисления площади заштрихованной области воспользуемся формулой (4.4)


 Пример 44. Вычислить площадь двух частей, на которые круг
Пример 44. Вычислить площадь двух частей, на которые круг  разделен параболой
разделен параболой  .
.
Решение. Сделаем чертеж (рис.4.6)
 - окружность с центром
- окружность с центром
в начале координат и радиусом  .
.
 - парабола, имеющая вершину
- парабола, имеющая вершину
в т.О(0,0)
Найдем точки пересечения параболы
и окружности:

 - не удовлетворяет условию
- не удовлетворяет условию  .
.
Если  , то
, то  или
или  ,
, 
Найдем площадь заштрихованной области по формуле (4.4), в которой изменены переменные интегрирования:

 ;
;
 .
.




 .
.
Найдем площадь второй (незаштрихованной) части, на которую круг разделен параболой


Вычисление площади фигуры, ограниченной линией,
Заданной параметрически
Пусть кривая задана параметрическими уравнениями 
 то площадь криволинейной трапеции, ограниченной этой кривой, прямыми
то площадь криволинейной трапеции, ограниченной этой кривой, прямыми  и
и  и отрезком [a,b] оси ОХ, выражается формулой
и отрезком [a,b] оси ОХ, выражается формулой
 , (4.5)
, (4.5)
где 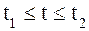 ,
,  ,
,  и
и  определяются из условий
определяются из условий 
 .
.
Пример 45. Найти площадь фигуры, ограниченной осью ОХ и одной аркой циклоиды

 .
.
Решение. Воспользуемся формулой (4.5). Предварительно найдем  :
:
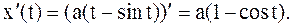


 (кв.ед.)
(кв.ед.)








