Самым распространенным в природе видом электромагнитного излучения является тепловое излучение, или лучеиспускание; оно совершается за счет энергии теплового движения атомов и молекул вещества, т. е. за счет внутренней энергии вещества, и потому ведет к охлаждению излучающего тела. Лучеиспускание присуще всем телам при любой температуре, отличной от абсолютного нуля. Тепловое излучение имеет сплошной спектр, однако распределение энергии в нем существенно зависит от температуры: при низких температурах тепловое излучение является преимущественно инфракрасным, при высоких температурах — видимым и ультрафиолетовым.
Всякое тело, излучая само, вместе с тем поглощает часть лучистой энергии, испускаемой другими (окружающими) телами; этот процесс называется лучепоглощением. Он ведет к нагреванию данного тела.
Очевидно, что, теряя энергию путем лучеиспускания и в то же время получая энергию путем лучепоглощения, данное тело должно в конце концов прийти в состояние теплового, или лучистого, равновесия, при котором потеря энергии за счет лучеиспускания компенсируется притоком энергии за счет лучепоглощения. Температура, соответствующая этому состоянию, называется температурой лучистого равновесия.
Воображаемое тело, поглощающее при любой температуре всю падающую на него лучистую энергию, называется абсолютно черным телом\ лучепоглощательная способность такого тела для всех длин волн одинакова и равна единице (Лх = А = 1). Для видимой части спектра телом, близким по своим свойствам к абсолютно черному, является сажа (А = 0,95).
Практически наиболее совершенным абсолютно черным телом является малое отверстие в рИс. 352 стенке замкнутой полости, внутренняя поверхность которой зачернена (рис. 352). Луч, попавший в отверстие, многократно отражается стенками полости и практически не выходит обратно, поскольку при каждом отражении значительная часть его энергии поглощается стенками
Абсолютно черное тело, поглощая падающую на него лучистую энергию, вместе с тем само излучает. Поэтому при низкой температуре полости отверстие в ней кажется черным; если же полость нагрета до высокой температуры, то отверстие представляется ярко светящимся. Примерами практически абсолютно черных тел могут служить зрачок глаза и смотровое отверстие мартеновской печи.
Закон излучения Кирхгофа -Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы. Известно, что при падении электромагнитного излучения на некоторое тело часть его отражается, часть поглощается и часть может пропускаться. Доля поглощаемого излучения на данной частоте называется поглощательной способностью тела 
. С другой стороны, каждое нагретое тело излучает энергию по некоторому закону 
, именуемым излучательной способностью тела.
Величины и могут сильно меняться при переходе от одного тела к другому, однако согласно закону излучения Кирхгофа отношение испускательной и поглощательной способностей не зависит от природы тела и является универсальной функцией частоты (длины волны) и температуры:
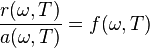
По определению, абсолютно чёрное тело поглощает всё падающее на него излучение, то есть для него 
. Поэтому функция 
совпадает с излучательной способностью абсолютно чёрного тела, описываемой законом Стефана — Больцмана, вследствие чего излучательная способность любого тела может быть найдена исходя лишь из его поглощательной способности.
Законы излучения абсолютно черного тела. Гипотеза Планка
Законы излучения абсолютно чёрного тела[править | править вики-текст]
Классический подход[править | править вики-текст]
Изначально к решению проблемы были применены чисто классические методы, которые дали ряд важных и верных результатов, однако полностью решить проблему не позволили, приведя в конечном итоге не только к резкому расхождению с экспериментом, но и к внутреннему противоречию — так называемой ультрафиолетовой катастрофе.
Изучение законов излучения абсолютно чёрного тела явилось одной из предпосылок появления квантовой механики.
Первый закон излучения Вина[править | править вики-текст]
В 1893 году Вильгельм Вин, воспользовавшись, помимо классической термодинамики, электромагнитной теорией света, вывел следующую формулу:
· 
где u ν — плотность энергии излучения,
ν — частота излучения,
T — температура излучающего тела,
f — функция, зависящая только от частоты и температуры. Вид этой функции невозможно установить, исходя только из термодинамических соображений.
Первая формула Вина справедлива для всех частот. Любая более конкретная формула (например, закон Планка) должна удовлетворять первой формуле Вина.
Из первой формулы Вина можно вывести закон смещения Вина (закон максимума) и закон Стефана — Больцмана, но нельзя найти значения постоянных, входящих в эти законы.
Исторически именно первый закон Вина назывался законом смещения, но в настоящее время термином «закон смещения Вина» называют закон максимума.
Второй закон излучения Вина[править | править вики-текст]
В 1896 году Вин на основе дополнительных предположений вывел второй закон:
где C 1, C 2 — константы. Опыт показывает, что вторая формула Вина справедлива лишь в пределе высоких частот (малых длин волн). Она является частным конкретным случаем первого закона Вина.
Позже Макс Планк показал, что второй закон Вина следует из закона Планка для больших энергий квантов, а также нашёл постоянные C 1 и C 2. С учётом этого, второй закон Вина можно записать в виде:
где h — постоянная Планка,
k — постоянная Больцмана,
c — скорость света в вакууме.
Закон Рэлея — Джинса[править | править вики-текст]
Основная статья: закон Рэлея — Джинса
Попытка описать излучение абсолютно чёрного тела исходя из классических принципов термодинамики и электродинамики приводит к закону Рэлея — Джинса:
Эта формула предполагает квадратичное возрастание спектральной плотности излучения в зависимости от его частоты. На практике такой закон означал бы невозможностьтермодинамического равновесия между веществом и излучением, поскольку согласно ему вся тепловая энергия должна была бы перейти в энергию излучения коротковолновой области спектра. Такое гипотетическое явление было названо ультрафиолетовой катастрофой.
Тем не менее закон излучения Рэлея — Джинса справедлив для длинноволновой области спектра и адекватно описывает характер излучения. Объяснить факт такого соответствия можно лишь при использовании квантово-механического подхода, согласно которому излучение происходит дискретно. Исходя из квантовых законов можно получить формулу Планка, которая будет совпадать с формулой Рэлея — Джинса при 
.
Этот факт является прекрасной иллюстрацией действия принципа соответствия, согласно которому новая физическая теория должна объяснять всё то, что была в состоянии объяснить старая.
Закон Планка[править | править вики-текст]
Основная статья: Формула Планка
Интенсивность излучения абсолютно чёрного тела в зависимости от температуры и частоты определяется законом Планка:
где 
— мощность излучения на единицу площади излучающей поверхности в единичном интервале частот в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с−1·м−2·Гц−1·ср−1).
Эквивалентно,
где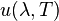 
— мощность излучения на единицу площади излучающей поверхности в единичном интервале длин волн в перпендикулярном направлении на единицу телесного угла (размерность в СИ: Дж·с−1·м−2·м−1·ср−1).
Полная (т.е. испускаемая во всех направлениях) спектральная мощность излучения с единицы поверхности абсолютно чёрного тела описывается этими же формулами с точностью до коэффициента π: ε(ν, T) = π I (ν, T), ε(λ, T) = π u (λ, T)[5].
