Поляриза́ция волн — характеристика поперечных волн, описывающая поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.
В продольной волне поляризация возникнуть не может, так как направление колебаний в этом типе волн всегда совпадает с направлением распространения.[1]
Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Волновой вектор показывает направление распространения волны, а вектор поляризации представляет собой вектор напряженности электрического поля. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.
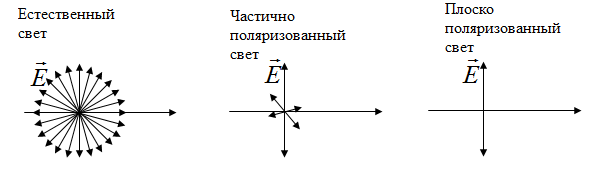
Поляризованным называется свет, в котором направления колебания вектора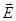 
упорядочены каким-либо образом.
Свет представляет собой суммарное электромагнитное излучение множества атомов. Атомы излучают световые волна независимо друг от друга, поэтому световая волна, излучаемая телом в целом, характеризуется всевозможными равновероятными колебаниями светового вектора 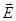. Свет со всевозможными равновероятными ориентациями вектора называется естественным. Свет, в котором имеется преимущественное направление колебаний вектора 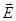и незначительная амплитуда колебаний вектора 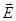в других направлениях, называется частично поляризованным.
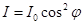- закон Малюса
Закон Малюса: Интенсивность света, прошедшего через поляризатор, прямо пропорциональна произведению интенсивности падающего плоско поляризованного света I 0 и квадрату косинуса угла между плоскостью падающего света и плоскостью поляризатора.
Если на поляризатор падает естественный свет, то интенсивность вышедшего из поляризатора света I 0 равна половине I ест, и тогда из анализатора выйдет
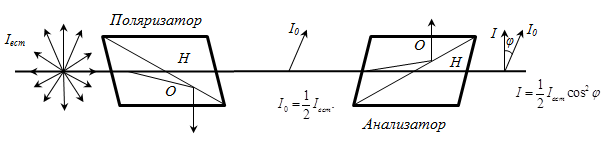
Поляризация при двойном лучепреломлении. Построения Гюйгенса для изотропной и анизотропной сред
Поляризация при двойном лучепреломлении. Обыкновенный и необыкновенный лучи.
Двойно́е лучепреломле́ние — эффект расщепления в анизотропных средах луча света на две составляющие. Впервые обнаружен датским ученым Расмусом Бартолином на кристалле исландского шпата. Если луч света падает перпендикулярно к поверхности кристалла, то на этой поверхности он расщепляется на два луча. Первый луч продолжает распространяться прямо, и называется обыкновенным (o — ordinary), второй же отклоняется в сторону, и называется необыкновенным (e — extraordinary).
Построение Гюйгенса.
Найти направление луча и волнового фронта в кристалле можно и графически, если воспользоваться принципом Гюйгенса.
(1629-1695 гг) предложил принцип, позволяющий по данному положению волнового фронта найти его положение в последующие моменты времени. По Гюйгенсу; всякая точка, которой достиг волновой фронт, может рассматриваться как самостоятельный источник элементарных волн: новый фронт волны представляет собой огибающую всех элементарных волн. Для одноосных кристаллов Гюйгенс предположил, что обыкновенному лучу соответствует волновая поверхность в виде сферы, а необыкновенному – в виде эллипсоида вращения. Форма волновых поверхностей (точнее – их сечений) для одноосного кристалла показана на рисунке.
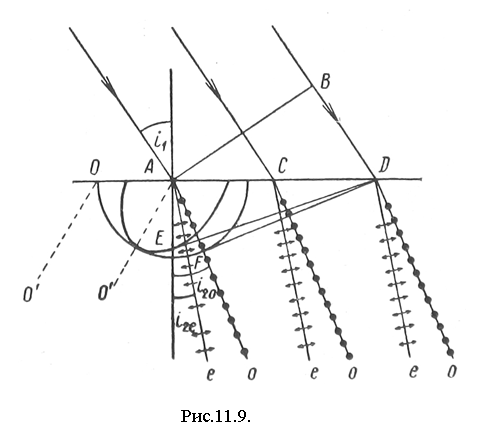
Пример построения Гюйгенса для частного случая показан на рис. 11.9. Обратите внимание – луч определяется как отрезок прямой. проведенной из точки А в точку касания волновой поверхности (результирующей волны) и волновой поверхности элементарного источника. На рисунке показано направление соответствующих лучей. Направление же перемещения фронта волны – это направление нормали к поверхности волнового фронта. Видно, что для обыкновенного луча эти два направления совпадают, а для необыкновенного – нет.
