(l˃˃b)
Нехай на нескінченно довгу щілину падає плоска електромагнітна хвиля. За щілиною розташуємо збиральну лінзу і у її фокальній площині екран паралельний до площини щілини. Розглянемо поперечний переріз щілини, що проходить через оптичний центр лінзи. Розіб’ємо відкриту частину хвильової поверхні на елементарні зони шириною dx паралельно до країв щілини. Вторинні хвилі, що випромінюються електронними запалами під кутом φ, зберуться у точці  екрана, кожна елементарна зона створює у точці
екрана, кожна елементарна зона створює у точці  коливання dE. Обмежимося малими кутами дифракції φ. Амплітуда коливань, які збуджуються елементарною зоною в будь якій точці екрану, залежать тільки від елементарної зони, площа пропорційна dx.
коливання dE. Обмежимося малими кутами дифракції φ. Амплітуда коливань, які збуджуються елементарною зоною в будь якій точці екрану, залежать тільки від елементарної зони, площа пропорційна dx.
Амплітуда d  коливання dE виражається як
коливання dE виражається як
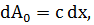
Якщо  – алгебраїчна сума амплітуд коливань, що збуджуються в точці
– алгебраїчна сума амплітуд коливань, що збуджуються в точці  всіма елементарними зонами щілини, то
всіма елементарними зонами щілини, то
 ,
, 
Знайдемо фазові співвідношення між коливаннями dE. Порівняємо фази коливань, що збуджуються в точці  двома елементарними зонами з координатами 0 і x. Оптичні шляхи 0P і QP- однакові (таутохронні), різниця фаз утворюється на шляху xsinφ. Якщо фазу коливань, що збуджуються елементарною зоною з координатою x0 вважатимемо рівною ωt, то фаза коливання, що збуджуються зоною з координатою x, буде
двома елементарними зонами з координатами 0 і x. Оптичні шляхи 0P і QP- однакові (таутохронні), різниця фаз утворюється на шляху xsinφ. Якщо фазу коливань, що збуджуються елементарною зоною з координатою x0 вважатимемо рівною ωt, то фаза коливання, що збуджуються зоною з координатою x, буде
ωt -  x sinφ,
x sinφ,
де x sinφ=  , (
, ( ˂
˂ 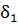 )
)

Коливання dE, що збуджується елементарною зоною з координатою х у точці  екрана виражається так:
екрана виражається так:
dE = 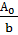 cos(ωt – xsinφ)
cos(ωt – xsinφ) 
Напруженість електричного поля для всієї щілини у точці  рівна сумі електричних напруженостей створених усіма елементарними зонами:
рівна сумі електричних напруженостей створених усіма елементарними зонами:
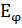 =
=  =
= 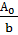 (-
(-  )ˣ
)ˣ
ˣ [sin(ωt –  bsinφ) – sin
bsinφ) – sin  ] =
] = 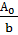
 2sin
2sin  cos(
cos( -
-  ) =
) =  cos(
cos( -
- 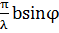 )
)
Амплітуда хвилі змінюється періодично зі зміною φ, I~  змінюється теж періодично.
змінюється теж періодично.
Позначимо u = 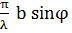
 =
= 
 ; (1)
; (1)
I(φ) = 
Знайдемо максимуми і мінімуми амплітуди, розглянувши екстремуми функції (1).
 =
= 
 = 0
= 0
 =
= 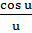 –
–  =
=  (ctg u –
(ctg u –  ) = 0
) = 0

а) Розглянемо випадок φ = 0, u = 0
 =
= 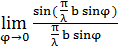 = 1,
= 1,
A =  (sin u ≈ u)
(sin u ≈ u)
Для усіх хвиль буде максимум. Отже φ = 0 – max
б) Інші максимуми: tg u = u. Рівняння розв’яжемо графічно
(ξ на малюнку відповідає u у формулах)
u = 0; 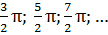
u ≈ 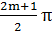 , m = 1, 2, 3, …
, m = 1, 2, 3, …
 = ±
= ± 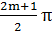
Максимуми:
 =±
=± 
 – max (2)
– max (2)
min:  = 0, коли sin u = 0; u ≠ 0
= 0, коли sin u = 0; u ≠ 0
u = π m
 = ± π m
= ± π m
 =
=  --min, m ≠ 0, m = ±1, ±2, ±3, … (3)
--min, m ≠ 0, m = ±1, ±2, ±3, … (3)
З формули (2) видно, що відстань між максимумами зростає, коли зменшується 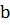 .
.
Якщо  ≤ λ не буде жодного мінімуму (m ≤ 1). Центральний максимум протягнеться до країв екрана.
≤ λ не буде жодного мінімуму (m ≤ 1). Центральний максимум протягнеться до країв екрана.
При зменшенні b зменшиться освітленість екрана.
При b>>λ збільшиться кількість максимумів і мінімумів, центральний максимум буде вузький з великою інтенсивністю.

Інтенсивності максимумів:
φ = 0, A =  (
(
 : sin φ =
: sin φ =  ,
,  =
=  =
=  ,
, 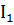 ~
~  ~ (0,21
~ (0,21  )² ≈ 0.045
)² ≈ 0.045 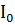
Якщо на щілину падає біле світло, максимуми для різних λ утворюються під різними кутами. Дифракційна картинка буде являти собою сукупність спектрів.
При зміщенні щілини відносно екрана, дифракційна картинка залишиться нерухомою. При зміщенні лінзи відносно щілини, дифракційна картинка на екрані зміщується.






