Короткі теоретичні відомості

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Кафедра Фотоніки

Лабораторна робота № 6

з курсу „Спеціальні розділи фізики”

ДОСЛІДЖЕННЯ ЯВИЩА ДИФРАКЦІЇ СВІТЛА

ЛЬВІВ – 2013
Лабораторна робота №6

ДОСЛІДЖЕННЯ ЯВИЩА ДИФРАКЦІЇ СВІТЛА

Мета роботи: Ознайомитись з явищем дифракції світла. Дослідити дифракцію Фраунгофера на вузькій щілини, отворі та двох отворах.

 

Короткі теоретичні відомості

Дифракцією називається сукупність явищ, що спостерігаються при поширенні світла в середовищі з різними неоднорідностями (поблизу границь непрозорих або прозорих тіл, через малі отвори) і які пов’язані із зміною напрямку поширення світлових хвиль (порівняно з напрямком, передбаченим геометричною оптикою).

Дифракція, зокрема, приводить до огинання світловими хвилями перешкод і проникнення світла в область геометричної тіні.

Між інтерференцією і дифракцією немає суттєвої фізичної відмінності. Інтерференція хвиль – це перерозподіл інтенсивності, який виникає в результаті суперпозиції хвиль, що збуджуються скінченним джерелом когерентних джерел. Перерозподіл інтенсивності, який виникає внаслідок суперпозиції хвиль, що збуджуються когерентними джерелами, які розміщені неперервно, називається дифракцією хвиль.

В залежності від віддаленості джерела світла та площини спостереження від екрану з отвором розрізняють зони дифракції Фраунгофера і Френеля.

Дифракцію Фраунгофера спостерігають у дальній зоні, яка віддалена від екрану на відстань, що у багато раз більша за розміри апертури. Дифракція Френеля має місце у ближній зоні і поширюється до зони дифракції Фраунгофера. Дифракція Фраунгофера є по суті граничним випадком дифракції Френеля на великих віддалях від екрану. Зауважимо, що зона дифракції Френеля також починається на деякій віддалі від області тіні.

Отже, дифракція Фраунгофера – це дифракція плоских світлових хвиль, коли джерело світла і точка спостереження нескінченно віддалені від перешкоди, яка викликала дифракцію. Для здійснення дифракції Фраунгофера потрібно джерело світла помістити у фокусі збірної лінзи 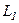, а дифракційну картину досліджувати у фокальній площині другої збірної лінзи 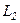, встановленої за перешкодою (рис. 229).

Нехай паралельний пучок монохроматичного світла падає по нормалі на непрозору плоску поверхню, в якій прорізано вузьку щілину ВС, що має сталу ширину а=ВС і довжину l>>а (рис. 1). За принципом Гюйгенса-Френеля точки щілини є вторинними джерелами хвиль, які коливаються в одній фазі, бо площина щілини збігається з фронтом падаючої хвилі.

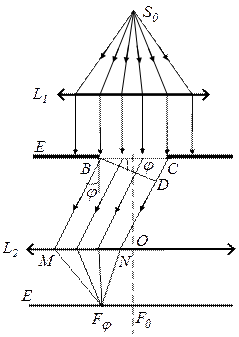
Рис. 1. Дифракція на щілині

 

У побічному фокусі лінзи 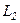збираються всі паралельні промені, які падають на лінзу під кутом 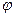до її оптичної осі O 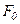, яка перпендикулярна до фронту падаючої хвилі. Оптична різниця ходу 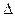між крайніми променями CN і BM, які поширюються від щілини в цьому напрямку, дорівнює , де ВD – перпендикуляр, який опущений з точки В на промінь CN.

Щілину ВС можна розбити на зони Френеля, які мають вигляд смуг, паралельних до ребра В щілини (рис. 2).

 

Рис.2.

 

Ширина кожної зони вибирається так, щоб різниця ходу від країв цих зон дорівнювала , тобто разом на ширині щілини поміститься 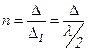зон.

Ширина кожної зони дорівнює 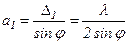, тобто їх площі однакові. Всі зони в заданому напрямку випромінюють світло однакової інтенсивності. При інтерференції світла від кожної пари сусідніх зон амплітуда результуючих коливань дорівнює нулю, бо ці зони спричиняють коливання з однаковими амплітудами, але протилежними фазами. Отже, результат інтерференції світла в точці визначиться тим, скільки зон Френеля вкладається в щілині. Якщо кількість зон парна, то n =2k і

, ,

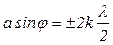в точці утвориться дифракційний мінімум. Знак „–” у правій частині відповідає променям світла, які поширюються від щілини під кутом – j і збираються в побічному фокусі 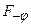лінзи, який симетричний відносно головного фокусу 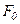. Якщо кількість зон непарна, то

, ,

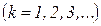в точці буде дифракційний максимум, інтенсивність якого 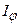і який відповідає дії однієї зони Френеля. Величина k називається порядком дифракційного максимуму.

У напрямку j=0 спостерігатиметься найінтенсивніший центральний максимум нульового порядку інтенсивністю 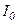оскільки коливання, які спричинюються в точці 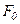всіма ділянками щілини, відбувається в одній фазі.

Залежність відношення 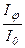від 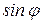зображено на рис. 3.

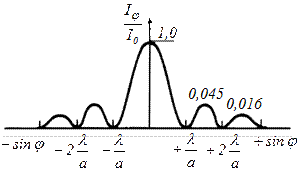
Рис.3.

 

 

Розрахунок показує, що інтенсивності центрального і наступних максимумів співвідносяться як

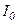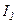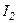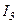: : : =1:0,045:0,016:0,0083:…,

тобто основна частина світлової енергії зосереджена в центральному максимумі.

Шириною дифракційного максимуму на екрані E називають відстань між двома найближчими до нього дифракційними мінімумами.

Ширина максимуму нульового порядку дорівнює відстані між двома мінімумами першого порядку, тобто . Отже, центральна світла смуга тим ширша, чим більша довжина хвилі 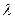і чим менша ширина щілини . В межах самої центральної смуги інтенсивність досить швидко зменшується від її середини до країв. При 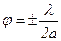інтенсивність дорівнює 0,4 від максимальної.

Для 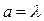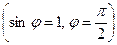головний максимум охоплює всю область екрана, тобто екран освітлений рівномірно. При збільшенні ширини щілини дифракційні смуги стають вужчими, а число мінімумів 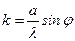зростає. Дифракційна картина стає яскравішою, оскільки через ширшу щілину проходить більший світловий потік. Коли щілина досить широка 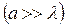, в центрі дифракційної картини буде чітке зображення джерела світла, що відповідає прямолінійному поширенню світла.

Ширина максимуму нульового порядку внаслідок дифракції на щілині при спостереженні на екрані, що розташований на відстані L від щілини (без лінзи) рівна:

У випадку білого світла буде спостерігатися сукупність відповідних картин для різних кольорів. Центральний максимум має райдужне забарвлення по краях. Повного гасіння світла не буде в жодній точці екрана, бо максимуми і мінімуми світла з різними l перекриваються.

 

При дифракції на отворі радіус центрального круга (радіус першого темного кільця) рівний:

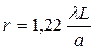
Період інтерференційної картини, яка утворюється при накладанні дифрагованих пучків від двох отворів рівний:

 

2. Опис установки

Оптична схема установки для спостереження дифракції Фраунгофера від однієї щілини у світлі лазера наведена на рис.1.

Паралельний пучок світла від He-Ne-лазера 1 падає нормально на щілину 2. Результат дифракції у вигляді періодичного розподілу інтенсивності світла спостерігається на екрані 3, який розміщений на відстані l > b²/ l від щілини 2 (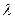 - довжина хвилі випромінювання лазера; 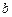– ширина щілини).

Фотодіод 4 можна механічно переміщати горизонтально в межах 100 мм в обидва боки від його середнього положення за допомогою мікрометричного гвинта. Для реєстрації переміщення фотодіода до направляючих механічного вузла, який містить мікрометричний гвинт, прикріплена масштабна лінійка з ціною поділки 1 мм.

 

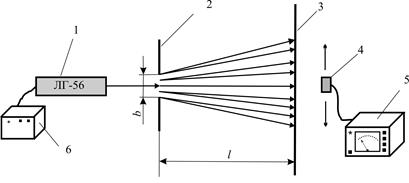
Рис.4. Оптична схема установки для спостереження дифракції Фраунгофера від однієї щілини

1 - Не-Ne лазер; 2 - розсувна щілина; 3 - екран з міліметровою шкалою; 4 - фотодіод; 5 - пристрій для реєстрації електричного сигналу з фотодіода; 6 - блок живлення лазера.

 

Порядок виконання роботи

1. Скласти оптичну схему у такій послідовності: лазер 1, розсувна щілина 2, екран 3. Щілину розмістити на відстані ~ 0,20 м від лазера, екран – майже на краю оптичної лави.

2. Увімкнути блок живлення 6 лазера. УВАГА! Через використання в лазері високої напруги (до 5000 В) слід бути гранично уважним і акуратним при виконанні роботи: така напруга небезпечна для життя.

3. Встановити щілину 2 таким чином, щоб пучок випромінювання від лазера 1 падав перпендикулярно на щілину і симетрично перекривав її.

4. Змінюючи мікрометричним гвинтом ширину щілини 2, отримати на екрані 3 чітку дифракційну картину. При цьому, відстань між мінімумами першого порядку повинна бути не менше 10 мм. УВАГА! Ні в якому разі не зводити мікрометричний гвинт до нуля – це веде до виходу з ладу щілини.

5. За показами мікрометричного гвинта визначити ширину щілини, виміряти відстань L від щілини 2 до екрана 3, а також відстані між першими 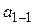, другими 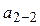, третіми 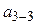і т.д. дифракційними мінімумами. Результати вимірювань записати в таблицю 1.

Таблиця 1

№
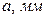
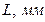
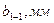
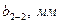
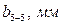
сер.	хххх

 

6. За шириною центрального максимуму розрахувати ширину щілини та порівняти з реальним розміром щілини. Ширину бокових пелюсток розрахувати теоретично та порівняти з експериментальними даними.

7. За експериментально визначеними значеннями a, L та b розрахувати довжину хвилі лазера. Порівняти з відомою довжиною хвилі гелій-неонового лазера та зробити висновки.

8. Розмістити на місці екрана 3 фотодіод 4 на рівні дифракційної картини.

9. Увімкнути пристрій 5, який призначений для реєстрації електричного сигналу з фотодіода 4 в мережу 220 В. Виміряти темновий струм фотодіода_.

10. Переміщаючи фотодіод 4 за допомогою мікрометричного гвинта вздовж дифракційної картини, зняти покази фотоструму 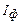в прямому і зворотному напрямках переміщення фотодіода. Вимірювання фотоструму 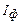проводити через 1 мм переміщення фотодіода. У випадку необхідності чутливість мікроамперметра змінити. Найменший відлік повинен відповідати не менше п’яти поділкам шкали мікроамперметра. Результати вимірювань записати в таблицю 2.

11. Побудувати графік розподілу інтенсивності світла 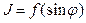в дифракційній картині. При побудові графіка вважати, що інтенсивність світла є пропорційною до величини фотоструму (врахувати значення темнового струму ). Значення 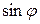при малих кутах дифракції 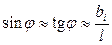( 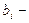відстань між положенням нульового максимуму і точкою на екрані, для якої робиться відлік фотоструму ).

12. Проаналізувати графік залежності та порівняти його з теоретичним графіком 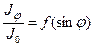, наведеним на рис.3. Зробити висновки.

Таблиця 2

№з/п								…

 

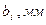
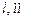
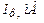
13. Встановити замість щілини екран з круглим отвором. За дифракційним полем від круглого отвору розрахувати діаметр отвору. Результати записати в таблицю.

14. Встановити в лазерний пучок екран з двома близько розміщеними отворами. Порахувати число інтерференційних смуг внаслідок дифракції на двох отворах та визначити період інтерференційних смуг. За розрахованим періодом визначити відстань між двома отворами. Результати записати в таблицю.

 

Контрольні запитання

1. Що таке дифракція світла?

2. Чим відрізняється дифракція Фраунгофера від дифракції Френеля?

3. За якої умови будуть спостерігатися дифракційні максимуми і мінімуми у випадку дифракції Фраунгофера на одній щілині?

4. Промені якої довжини хвилі при дифракції на одній щілині відхиляються від початкового напрямку поширення найбільше?

5. Як розподіляється інтенсивність світла в дифракційних максимумах при дифракції Фраунгофера на одній щілині?

6. Яка картина буде спостерігатися на екрані, якщо ширина щілини , ?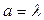

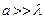7. Від чого залежить радіус першого темного кільця в дифракційній картині при дифракції на круглому отворі?

8. Від чого залежить період інтерференційних смуг, що утворюються при дифракції на двох отворах?