Экзаменационные билеты по геометрии. 7-й класс
Билет 1
- Определение равнобедренного треугольника. Свойство углов при основании равнобедренного треугольника. (1. Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя — основанием. 2. Свойства- Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой. Также равны биссектрисы, медианы и высоты, проведённые из этих углов.)
- Определение биссектрисы угла. Построение биссектрисы угла. (1.Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла. Биссектриса угла — геометрическое место точек внутри угла, равноудалённых от сторон угла. 2. Построение биссектрисы угла: a) берем произвольный раствор циркуля и описываем дугу с центром в вершине угла так, чтобы она пересекала стороны угла, b) этим же раствором проводим дуги с вершиной в точках пересечения исходной дуги со сторонами. Через точку, где эти две новые дуги пересеклись, проводим прямую, которая проходит и через вершину угла. Полученная прямая и будет биссектрисой угла.)
- Найдите величины смежных углов, если один из них в 5 раз больше другого.(Пусть меньший смежный угол равен х. Тогда другой будет равен 5х. По теореме о сумме смежных углов, получаем:
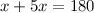
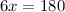
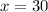 .
.
Мы нашли меньший угол. Теперь найдем больший: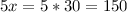
Ответ: 30, 150.)
Билет 2
- Определение смежных углов. Свойство смежных углов. (1.Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой. 2. Сумма смежных углов равна 180º.)
- Определение треугольника. Построение треугольника по трем сторонам. (1.Треугольник - это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, соединяющих эти точки.2. Для построения треугольника по трем сторонам с помощью циркуля и линейки мы будем использовать следующий алгоритм построения. (Алгоритм построения треугольника с помощью циркуля и линейки, раздаю каждому учащемуся))
- Отрезки MN и DK пересекаются в их общей середине B. Докажите равенство треугольников MDB и NKB. (Рассмотрим треуг. MDB и NKB: 1) МВ=BN по условию. 2) DВ=ВК по условию. 3) /_МВD=/_NBK т. к. вертикальные. Треугольник МDВ равен треугольнику NKB по двум сторонам и углу между ними.
Билет 3
- Определение вертикальных углов. Свойство вертикальных углов. (1. Углы, у которых стороны одного угла являются продолжением сторон другого угла, называются вертикальными. Свойство: вертикальные углы равны.)
- Определение перпендикулярных прямых. Построение прямой, проходящей через точку, не лежащую на данной прямой и перпендикулярную к данной прямой. (1.Перпендикулярными называются прямые, которые пересекаются под прямым углом.2. Допустим точка не лежащая на прямлй - точка А.
Берем ее центром окружности. Проводим окружность с цнтром в точке А, так что бы она пересекала прямую.
Получили на прямой еще две точки (пересечение с окружностью)
Теперь из этихточек проводим окружности одинакового радиуса, так чтобы они пересеклись друг с другом.
Теперь проводим прямую через точку А и точки пересечения маленьких двух окружностей, эта прямая будет перпендикулярна данной) - Найдите периметр равнобедренного треугольника ADC с основанием AD, если AD = 7 см, DC = 8 см. (Сторона АС = ДС (тр.-к равнобедренный). Периметр тр.-ка Р = АД + АС + ДС = 7 + 8 + 8 = 23(см)
Билет 4
- Определение равных треугольников. Признаки равенства треугольников (доказательство одного из признаков по выбору учащегося).
(Определения:
1. Два треугольника называются равными (Δ ABC = Δ A1B1C1), если у них соответствующие стороны равны
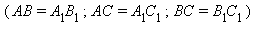
и соответствующие углы равны
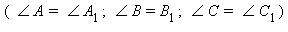
b Равные треугольники совпадают при наложении
Признаки равенства:
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.)
- Определение отрезка. Деление отрезка пополам. (Отрезок - Это ЧАСТЬ прямой, ограниченная с двух сторон. Деление отрезка пополам - это нахождение на отрезке середины)
- Найдите неразвернутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 126°. (Если углы не развернутые то они вертикальные, а вертикальные углы равны то есть углы = 126/2 =63градуса 1 и 2 угол)
Билет 5
- Определение медианы треугольника. Свойство медианы равнобедренного треугольника. (1Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. 2Медиана равнобедренного треугольника одновременно является биссектрисой и высотой этого треугольника.)
- Определение угла. Построение угла, равного данному. (1Угол — геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (которая называется вершиной угла.2 Если дана прямая, а не луч, то вершину нового угла можно выбрать на ней произвольно. Если же дан луч, то вершиной угла считается точка, от которой отложен луч.
Алгоритм построения угла, равного данному, на луче: a)Нарисовать окружность (или часть окружности) с центром в вершине данного угла так, чтобы она пересекла стороны данного угла. b)Нарисовать окружность (или ее часть) с тем же радиусом, что и в п. 1, но с вершиной в точке, от которой отложен луч. При этом луч и окружность должны иметь точку пересечению. c)Зафиксировать циркулем расстояние между точками пересечения окружности из п. 1 со сторонами данного угла.d)Нарисовать окружность (или ее часть) радиусом, полученным в п. 3, и с центром в точке пересечения данного луча и нарисованной в п. 2 окружности. При этом окружности (или их части) должны иметь точку пересечения.В точку пересечения двух окружностей, полученную в п. 4, провести новый луч из точки, от которой отложен данный по условию задачи луч. Эти два луча составляют угол, равный данному.
Чтобы доказать, что полученный угол равен данному, надо рассмотреть треугольники, образованные точками пересечения сторон угла и окружностей. Треугольники будут равны по трем сторонам.).
- Точки М, N и R лежат на одной прямой, MN = 11 см, RN = 20 см. Найдите расстояние MR. (11+20=31см-Значит MR=31см)
Билет 6
- Определение параллельных прямых. Признаки параллельности прямых (доказательство одного из признаков по выбору учащегося).(Параллельными прямыми называются прямые, которые лежат в одной плоскости, а также либо совпадают, либо не пересекаются. признак: Если внутренние накрестлежащие углы равны, то прямые параллельны.)
- Определение треугольника. Построение треугольника по стороне и двум углам. (Треугольник - это геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки. Построение: струятся сначала отрезок. Из первого его конца строим 1 угол. Из второго - 2 угол. затем лучи проведенные из концов отрезка пересекутся в одной точке. что даст нам 3ью вершину (1 и 2 - это концы отрезка). И соединив вершины мы получим треугольник.
- Угол, противолежащий основанию равнобедренного треугольника, равен 50°. Найдите величину внешнего угла при основании. (Угол при основании = (180-50) /2=65
Внешний угол при основании = 180-65 = 1150)
Билет 7
- Аксиома параллельных. Теоремы об углах, образованных двумя параллельными прямыми и секущей. (Доказательство одной из теорем по выбору учащегося.)
(Теорема:
1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.
3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°.
Доказательство
1. Пусть параллельные прямые a и b пересечены секущей MN (c). Докажем что накрест лежащие углы 3 и 6 равны. Допустим, что углы 3 и 6 не равны. Отложим от луча MN угол PMN, равный углу 6, так, чтобы угол PMN и угол 6 были накрест лежащими углами при пересечении прямых МР и b секущей MN. По построению эти накрест лежащие углы равны, поэтому МР||b. Мы выяснили, что через точку М проходят две прямые (прямые a и МР), параллельные прямой b. Но это противоречит аксиоме параллельных прямых. Значит, наше допущение неверно и угол 3 равен углу 6.
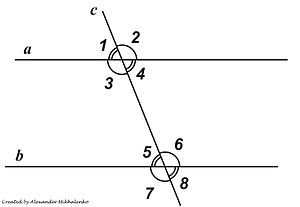 )
)
2 Определение треугольника. Построение треугольника по двум сторонам и углу между ними.
(1.Треугольник — геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.
2.Построение циркулем и линейкой: 1.Строим угол, равный данному.2.На сторонах угла откладываем длины заданных отрезков.3.Соединяем полученные точки отрезком.)
3 Найдите углы треугольника, на которые высота разбивает равносторонний треугольник. (У равностороннего треугольника все углы равны 60*. Высота делит треугольник под прямым углом. Поэтому у получившихся двух одинаковых треугольников будут три угла - один 60*, другой 90*, и третий 30* (так как он делится высотой на две половины))
Билет 8
- Определение треугольника. Теорема о сумме углов треугольника.
(1.Треугольник— геометрическая фигура, образованная тремя отрезками, которые соединяют три не лежащие на одной прямой точки.2. Теорема: Сумма углов треугольника равна 180°.
- Построение равнобедренного треугольника по боковой стороне и высоте, проведенной к основанию. Теорема (свойство высоты равнобедренного треугольника) Высота равнобедренного треугольника, проведенная к основанию, является его медианой и биссектрисой.
- Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них равен 42° (пусть прямые АВ и СД параллельны и пересекаются секущей КН в точках М и Т. пусть угол КМВ=42* по условию.
Тогда угол АМТ=КМВ=42*как вертикальные, угол АМК=180-42=138* как смежные в развернутом углу, угол ТМВ=АМК=138* как вертикальные. Угол МТД=КМВ=42*как соответствующие. Угол СТН=МТД=428 как вертикальные, угол МТС=180-42=138* как смежные, угол НТД=МТС=138* как вертикальные)
Билет 9
- Определение внешнего угла. Свойство внешнего угла. (1.Углы, смежные с углами треугольника, называются внешними.2. Свойства внешних углов треугольника:
Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна.
Сумма внешнего и внутреннего угла при одной вершине равна.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.)
- Определение медианы треугольника. Построение медианы треугольника.(1. Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.2. Чтобы построить медиану треугольника, надо:
1) С помощью линейки найти и отметить середину стороны треугольника.
2) Соединить полученную точку с вершиной, лежащей напротив этой стороны.)
- Найдите все углы, образованные при пересечении двух параллельных прямых секущей, если один из них 126°.(180-126=54. Итак: 126;54;126;54 - это не одной из параллейных линий и точно также на другой.)
Билет 10
- Определение прямоугольного треугольника. Свойство катета, лежащего напротив угла в 30°. (Свойства прямоугольного треугольника:
Сумма двух острых углов прямоугольного треугольника равна 90º
Сумма углов треугольника равна 180º, а прямой угол равен 90º, поэтому сумма двух острых углов прямоугольного треугольника равна 90º.
Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы.)
- Определение высоты треугольника. Построение высоты. (1.Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону.2.
Чтобы провести высоту в треугольнике ABC из заданной вершины B, выполните последовательно:
1.Установите раствор циркуля больше, чем расстояние от точки B до стороны AC, и проведите две дуги с центрами в точке B, пересекающие AC в точках P и Q.
2.Произвольным раствором циркуля проведите две дуги с центрами в точках P и Q, пересекающиеся в точке E.
3.Проведите прямую BE, пересекающую AC в точке H. Отрезок BH является высотой, опущенной из вершины B на сторону AC.)
- Найдите смежные углы, если один из них на 55° больше другого. (х+х+55=180 2х=125х=62,5 угол1=62,5 угол2=117,5 (62,5+55))
Билет 11
- Соотношение между сторонами и углами в треугольнике.(Теоремы.
Во всяком треугольнике:
1) против равных сторон лежат равные углы,
2) против большей стороны лежит больший угол.
Обратные теоремы.
Во всяком треугольнике:
1) против равных углов лежат равные стороны,
2)против большего угла лежит большая сторона.
Следствие 1.
В равностороннем треугольнике все углы равны.
Следствие 2.
В равноугольном треугольнике все стороны равны. - Построение прямой, проходящей через данную точку и параллельную данной прямой. (Через точку проводим перпендикуляр к данной прямой, и через точку проводим перпендикуляр построенного перпендикуляра)
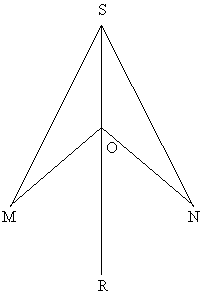
- Луч SR является биссектрисой угла S, а отрезки SM и SN равны. Докажите равенство треугольников SMO и SNO. (Отрезки SM и SN равны, углы равны, SO общая. Две стороны треугольника и угол между ними равны - значит треугольники равны.)
Билет 12
- Равнобедренный треугольник. Признак равнобедренного треугольника. (Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми, а третья сторона – основанием.
Признаки равнобедренного треугольника.
Теорема: Если в треугольнике два угла равны, то он равнобедренный.
Теорема: Если в треугольнике медиана является и высотой, то такой треугольник равнобедренный.
Теорема: Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
- Определение перпендикулярных прямых. Построение прямой, проходящей через точку, лежащую на данной прямой, перпендикулярно к данной прямой. (1.Две прямые которые при пересечении образуют прямые углы. 2. 1. Начертить прямую. 2. Отметить на ней точку, через которую нужно провести перпендикулярную к ней прямую.3. Циркулем отмерить от данной точки произвольным раствором по обе стороны от нее отрезки. 4. Из концов этих отрезков раствором циркуля, несколько больше первого, провести окружности с центрами в отмеченных точках (по обе стороны от данной)5. Точки пересечения этих окружностей по обе стороны от прямой соединить. Получился искомый перпендикуляр.)
- Найдите длину отрезка AM и градусную меру угла ABK, если BM – медиана, а BK – биссектриса треугольника ABC и известно, что AC = 17 см, угол ABC равен 84°. (В треугольнике АВС ВМ - медиана следовательно делит АС пополам АМ=АС/2=17/2=8,5-
угол ВК - биссектриса делит угол АВС пополам ABK =АВС/2=84/2=42 --угол ABK = 42 AM=8.5cm
Задачи 4 к экзаменационным билетам по геометрии. 7 класс
(Данные задачи ученик получает на экзамене)
Билет 1
Докажите равенство отрезков, соединяющих середину основания равнобедренного треугольника с серединами боковых сторон.
(Пусть ABC - равнобедренный треугольник с основанием AC, EN и EM - отрезки, соединяющие основание с соответственными сторонами: AB и BC. Нужно доказать равенство треугольников ANE и CME (из этого будет следовать и равенство отрезков); Они равны, т.к. по условию AE = СE (E -середина основания), углы BAE = BCE - углы при основании равнобедренного треугольника, AN = MC - по условию отрезки EN и EM соединяют середины боковых сторон, которые также равны.Треугольники ANE и CME равны, из этого следует, что EN = EM.)
Билет 2
Известно, что 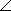 OAM =
OAM = 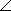 OAK и
OAK и 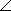 MBS =
MBS = 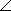 KBS. Докажите,что AK = AM, BM = BK.
KBS. Докажите,что AK = AM, BM = BK.
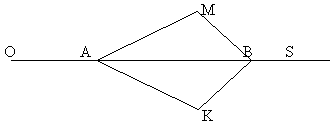
(Доказательство
Если ОАМ =ОАК значит МАВ=ВАК, так же равны МВА и КВА.
АВ - общая сторона, по второму признаку равенства треугольников, треугольники АМВ и АВК равны.
Значит: АК = АМ, ВМ = ВК.)
Билет 3
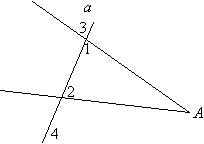
Прямая а пересекает стороны угла A. Докажите,что 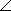 1 =
1 = 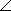 2, если известно, что
2, если известно, что 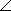 5 =
5 =  6.
6.
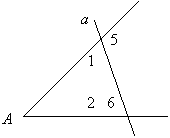
(Угол 1=углу 3(как вертикальные)
Угол 2=углу 4(как вертикальные)
А т.к. угол 3=4, то и 1=2)
Билет 4
Отрезки AB и CM пересекаются в точке O. Луч OK является биссектрисой угла MOB. Найдите угол MOK, если угол AOM равен 86°.(Т.к. угол AOM=86°, то угол смежный с ним BOM равен 180°-86°=94° Т.к. OK - биссектриса, то угол BOK=углу MOK=94°/2=47° Ответ: 47°)
Билет 5
Прямая а пересекает стороны угла А. Докажите,что  1 =
1 =  2, если известно, что
2, если известно, что 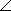 3 =
3 = 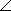 4.
4.
Билет 6
Найдите углы при основании MP равнобедренного треугольника МОР, если MK – его биссектриса и 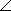 OKM = 96°. (Угол 1=углу 3(как вертикальные) угол 2=углу 4(как вертикальные) а т.к. угол 3=4, то и 1=2
OKM = 96°. (Угол 1=углу 3(как вертикальные) угол 2=углу 4(как вертикальные) а т.к. угол 3=4, то и 1=2
Билет 7
В треугольнике MOK 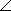 O = 76°, а угол M в 3 раза меньше внешнего угла при вершине K. Найдите неизвестные углы треугольника.(Пусть х -угол М
O = 76°, а угол M в 3 раза меньше внешнего угла при вершине K. Найдите неизвестные углы треугольника.(Пусть х -угол М
Тогда 3х - внешний угол при вершине угла К
180-3х - угол К
Сумма всех углов треугольника=180
Составим уравнение:
х+(180-3х)+76=180
х+180-3х+76=180
-2х=-76
х=38° - угол М
180-(76+38)=66° - угол К
Билет 8
Отрезки AB и CM параллельны и равны.Докажите, что AM = BC.
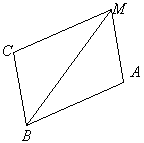
(Т. к оба отрезка лежат в одной плоскости и не пересекаются. Притом по условию они равны следовательно они параллельны и равны)
Билет 9
Докажите, что AB = CM.

(АВ = СМ, потому что




