Существуют устройства (демпферы), которые создают силу пропорциональную относительной скорости  (рис.17). Коэффициент пропорциональности называется коэффициентом демпфирования или коэффициентом вязкого сопротивления.
(рис.17). Коэффициент пропорциональности называется коэффициентом демпфирования или коэффициентом вязкого сопротивления.

Рис.17
Дифференциальное уравнение движения точки с массой m, закрепленной на упругом элементе и демпфере имеет вид:
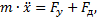

Начальные условия имеют вид: t=0, 
Характеристическое уравнение имеет вид:  .
.
Корни характеристического уравнения равны: 
Рассмотрим возможные решения:
1-й случай 
Решение имеет вид:

 - условная амплитуда затухающих колебаний;
- условная амплитуда затухающих колебаний;
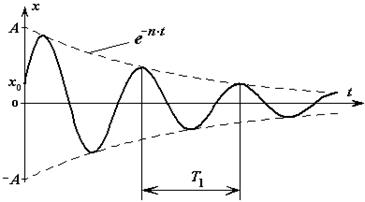
Рис.18
 - круговая или циклическая частота затухающих колебаний. Измеряется в рад/сек.
- круговая или циклическая частота затухающих колебаний. Измеряется в рад/сек.
 - фазовый угол (или просто фаза).
- фазовый угол (или просто фаза).
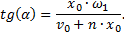
 - период затухающих колебаний (рис.18).
- период затухающих колебаний (рис.18).
 - частота колебаний (1 колеб/cек=1 Гц)
- частота колебаний (1 колеб/cек=1 Гц)

 - логарифмический декремент колебаний.
- логарифмический декремент колебаний.
Материальная точка совершает гармонические колебания с частотой  и амплитудой, величина которой все время убывает.
и амплитудой, величина которой все время убывает.
Движение изображающей точки на фазовой плоскости показано на рис. 19.
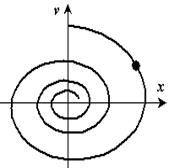
Рис.19
2-й случай 
Решение имеет вид:

Материальная точка совершает затухающее неколебательное движение (рис.39).

Рис.20
3-й случай  (два одинаковых корня)
(два одинаковых корня)
Решение имеет вид:
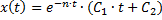
Материальная точка так же совершает затухающее неколебательное движение (рис.20).
Вынужденные колебания с вязким сопротивлением.
Рассмотрим движение точки под действием трех сил: одна восстанавливающая сила, вторая - сила демпфирования (сила вязкого сопротивления), а третья зависит от времени.  - гармоническая возмущающая сила.
- гармоническая возмущающая сила.
F0 - амплитуда возмущающей силы.
 - круговая частота возмущающей силы.
- круговая частота возмущающей силы.

Рис.21
Дифференциальное уравнение движения точки с массой m, закрепленной на упругом элементе и демпфере (рис.21), под действием возмущающей гармонической силы имеет вид:

Задавая решение уравнения в виде:  и подставляя его в дифференциальное уравнение получим алгебраическое уравнение для определения амплитуды вынужденных колебаний.
и подставляя его в дифференциальное уравнение получим алгебраическое уравнение для определения амплитуды вынужденных колебаний.

Разделим его на массу и обозначим  тогда
тогда  и окончательно
и окончательно
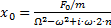 - амплитуда вынужденных колебаний.
- амплитуда вынужденных колебаний.
 - частота собственных колебаний
- частота собственных колебаний
Материальная точка колеблется с амплитудой  и частотой возмущающей силы
и частотой возмущающей силы  .
.
Построим зависимость модуля амплитуды  от частоты возмущающей силы
от частоты возмущающей силы  (рис.22).
(рис.22).

Рис.22
Модуль амплитуды вынужденных колебаний возрастает от  (при
(при  ) до некоторой величины, а затем убывает до нуля (при
) до некоторой величины, а затем убывает до нуля (при  ).
).
Примеры решения задач
Пример 1. Колебания материальной точки происходят относительно положения равновесия по закону х=А∙sinωt с периодом T=12 с. Определить, за какой наименьший промежуток времени t1 точка удалится от положения равновесия на расстояние, равное половине амплитуды x=A/2. За какой промежуток времени t2 она пройдет оставшуюся часть пути до максимального отклонения.
Найти: t1-? t2-?
Решение. В момент времени t1 cмещение равно А/2: А/2=А∙sinωt1, sinωt1=1/2, т.е. ωt1=π/6, или (2π/Т)t1=π/6.
Отсюда t1=T/12=1 c.
Расстояние от точки равновесия до точки максимального отклонения материальная точка проходит за t=T/4. Следовательно, t2=T/4- T/12= 2 c.
Пример 2. За какую часть периода точка, совершающая гармонические колебания по закону косинуса, сместится на половину амплитуды, если в начальный момент она находилась в положении равновесия?
Решение. Колебания точки описываются уравнением x=Acos(ω0t+α). Поскольку при t = 0 смещение х = 0, то начальная фаза φ должна равняться π /2, т.е. уравнение имеет вид:
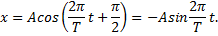
По условию смещение x=A/2, следовательно, 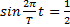 (знак «минус» не учитываем, т.к. нас интересует первое попадание колеблющейся частицы в данное положение).
(знак «минус» не учитываем, т.к. нас интересует первое попадание колеблющейся частицы в данное положение).
Отсюда  и
и 
Пример 3. Точка совершает колебания по закону x=5cosω0t (м), где ω0= 2 с–1. Определить ускорение точки в момент времени, когда ее скорость равна 8 м/с.
Решение. Зависимости скорости и ускорения колеблющейся точки от времени задаются уравнениями

и при α=0

Следовательно,  . Тогда
. Тогда  и с учетом того, что α=0, получаем
и с учетом того, что α=0, получаем 
Пример 4. Максимальная скорость точки, совершающей гармонические колебания, равна 10 см/с, максимальное ускорение равно 100 см/с2. Найти циклическую частоту колебаний, их период и амплитуду.
Решение. Из формул
x=Acos(ω0t+α),
v=-Acos(ω0t+α)=-vmaxsin(ω0t+α),
a=-A  cos(ω0t+α)=- amaxcos(ω0t+α),
cos(ω0t+α)=- amaxcos(ω0t+α),
видно, что xmax=A; vmax=Aω; amax=Aω2.

Откуда ω0=10 с–1.
Период 
Амплитуда 
Пример 5. Амплитуда гармонических колебаний материальной точки А = 0,02 м, полная энергия колебаний W=3∙10–7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F= 2,25 ∙ 10–5 Н?
Решение. Из  можно выразить
можно выразить 
Тогда, используя выражение F=-kx, получим

Искомое смещение

Пример 6. В качестве физического маятника используется стержень, подвешенный за один из его концов. Чему равен период колебаний при длине стержня 1 м?
Решение. Для того, чтобы воспользоваться формулой  , необходимо по теореме Штейнера посчитать момент инерции стержня относительно оси, проходящей через точку подвеса:
, необходимо по теореме Штейнера посчитать момент инерции стержня относительно оси, проходящей через точку подвеса:
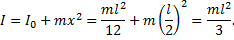
Тогда, учитывая, что x= l /2,

Пример 7. Два одинаково направленных гармонических колебания заданы уравнениями x1=A1∙sinω0t и x2=A2∙cosω0t, где А1 = 1 см; А2 = 2 см; ω0 = 1 с–1. Определить амплитуду результирующего колебания А, его частоту v и начальную фазу α. Найти уравнение этого движения.
Решение. Преобразуем первое уравнение, заданное в условии задачи, к виду x=A∙cos(ω0t+α) и получим

Тогда по формуле  амплитуда результирующего колебания:
амплитуда результирующего колебания:

=1+4+2∙2∙cos0,5π=5 см2.
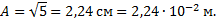
Частота результирующего колебания равна частоте складывающихся колебаний

Начальную фазу находим по формуле:

Начальная фаза α=arctg(-0,5)=-26,6°=-0,46 рад.
Уравнение результирующего колебания имеет вид x=2,24∙10-2cos(t-0,46) м.
Пример 8. Складываются два колебания одинакового направления (рис.23), выражаемых уравнениями x1=A1cosω(t+τ1) и x2=A2cosω(t+τ2), где А1=1 см; А2=2 см; τ1=1/6 с; τ2=1/2 с; ω=π рад/с. Определить начальные фазы φ1 и φ2 составляющих колебаний; найти амплитуду А и начальную фазу φ результирующего колебания.
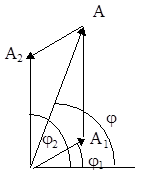
Рис.23
Решение. Уравнение гармонического колебания имеет вид:
х=А∙cos(ωt+φ) (1)
Преобразуем уравнения, заданные в условии задачи, к такому же виду:
x1=A1cos(ωt+ωτ1) и x2=A2cos(ωt+ωτ2) (2)
Из сравнения выражений (2) с (1) находим начальные фазы первого и второго колебаний: φ1=ωτ1=π/6 рад и φ2= ωτ2=π/2 рад.
Для определения амплитуды А результирующего колебания удобно воспользоваться векторной диаграммой, представленной на рис.23.
Согласно теореме косинусов, получим:

φ2-φ1=π/3 рад.
Подставим значения А1, А2 и φ2-φ1 в (3), извлечем корень и получим: А=2,65 см.
Тангенс начальной фазы результирующего колебания определим непосредственно из рисунка 41.1:

Тогда φ=arctg(5/  )=70,9°=0,394π рад.
)=70,9°=0,394π рад.
Так как циклические частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту ω.
Это позволяет написать уравнение результирующего колебания в виде х=А∙cos(ωt+φ),
где А=2,65 см, ω=π рад/с, φ=0,394π рад.
Пример 9. Шарик массой m=10-2 кг=10 г совершает гармонические колебания с амплитудой А=0,2 м и периодом Т=4 с. В начальный момент времени t=0: х=А. Найти кинетическую и потенциальную энергию в момент времени t= 1 с.
Найти: Ек-? Еп-?
Решение: Запишем уравнение гармонических колебаний
х=Аcos(ωt+φ0), где ω=2π/Т.
Т.к. при t=0 х=А, то можно определить начальную фазу Асоs(ω∙0+φ0)=A, соsφ0=1, φ0=0.
Таким образом, х=0,2cos[(2π/4)t]= 0,2cos[(π/2)t] (м).
Кинетическая энергия шарика определяется по формуле: Ек=mv2/2, где v=dx/dt=-Aω∙sinωt.
Ек=[mA2ω2∙sin2ωt]/2=5∙10-3 Дж.
Потенциальная энергия шарика равна:
Еп=kx2/2=[kА2cos2ωt]/2=[kА2cos2(π/2)]/2,
Еп=0.
Пример 10. Физический маятник представляет собой стержень длиной l= 1 м и массой mc=3m1 с прикрепленным к одному из его концов обручем диаметром d= l/2 и массой mо=m1. Горизонтальная ось ОZ проходит через середину стержня перпендикулярно ему (рис. 24). Определить период колебаний такого маятника T -?.
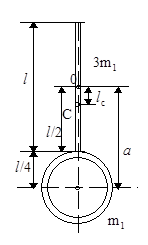
Рис.24
Решение. Период колебаний физического маятника определяется по формуле

где J - момент инерции маятника относительно оси колебаний, m - его масса, lc - расстояние от центра масс маятника до оси колебаний. Момент инерции маятника равен сумме моментов инерции стержня J1 и обруча J2:
J=J1+J2. (2)
Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его центр масс, определяется по формуле J1=mc l 2/12, т.е. J1=m1 l 2/4.
Момент инерции обруча найдем, воспользовавшись теоремой Штейнера J=Jo+m a 2. Применив эту формулу к обручу, получим
J2=m1(l /4)2+ m1(3 l /4)2 = (5/8)m1 l 2.
Подставив выражения J1 и J2 в формулу (2), найдем момент инерции маятника относительно оси вращения:
J= m1 l 2/4+(5/8)m1 l 2=(7/8)m1 l 2.
Расстояние l c от оси маятника до его центра масс равно
l c=(Σmixi)/Σmi=(3m1∙0 + m1(3 l /4))/(3m1+m1)=(3/16) l.
Подставив в формулу (1) выражения J, Jc и массы маятника (m=3m1+m1=4m1), найдем период его колебаний:

После вычисления по этой формуле получим Т=2,17 с.
Пример 11. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях (рис.25), выражаемых уравнениями x=2cosω0t (см) и y=sinω0t (см). Найти уравнение траектории точки и построить ее, указав направление движения, если ω0=π/3 (с–1).

Рис.25
Решение. Преобразуем второе уравнение к виду y=Аcos(ω0t+α) и получим:

Как видно, разность фаз складывающихся колебаний α= -π/2 и это соответствует частному случаю, когда уравнение траектории имеет вид:  . Траекторией движения в этом случае является эллипс, приведенный к главным осям, уравнение которого
. Траекторией движения в этом случае является эллипс, приведенный к главным осям, уравнение которого  .
.
Для того, чтобы указать направление движения точки, необходимо проследить, как меняется ее положение с течением времени. Для этого найдем координаты точки для двух ближайших моментов времени. Период результирующих колебаний  Поэтому моменты времени, отличающиеся на одну секунду, можно считать достаточно близкими.
Поэтому моменты времени, отличающиеся на одну секунду, можно считать достаточно близкими.
При t=0: x1=2cos0=2; y1=1cos(-π/2)=0;
При t=1 c: x2=2cos(π/3)=1; y2=1cos(π/3-π/2)=1cos(-π/6)=0,86.
Следовательно, точка 1 имеет координаты (2; 0), а точка 2 – (1; 0,86). Это означает, что движение происходит против часовой стрелке.
Пример 12. Амплитуда колебаний математического маятника длиной 1 м за время 10 мин уменьшилась в 2 раза. Определить коэффициент затухания, логарифмический декремент затухания колебаний и количество колебаний, совершенных за это время. Записать уравнение колебаний, если в начальный момент маятник был отведен из положения равновесия на 5 см и отпущен.
Решение. Период и частоту колебаний математического маятника найдем из выражения:

Запишем отношение амплитуд (начальной A0=5 см и через время t = 10 мин = 600 с):

следовательно, βt=ln2, отсюда

Количество колебаний N, совершенных за время t, найдем из того, что t=NT, а, значит, βNT=ln2, и тогда

Логарифмический декремент затухания определим по:
δ=βT=2∙10-3.
Выбор гармонической функции для написания уравнения колебаний проведем на основании того, что в начальный момент смещение точки от положения равновесия равно амплитуде, а этому условию удовлетворяет функция косинус. Тогда уравнение данных затухающих колебаний имеет вид: x=5∙10-2e-0,001tcosπt (м).
Пример 13. Пружинный маятник, (жесткость пружины которого равна k = 10 Н/м, а масса груза m = 100 г) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r = 0,02 кг/с. Определить коэффициент затухания β и резонансную амплитуду Арез, если амплитудное значение вынуждающей силы F0 = 10 мН.
Решение. Коэффициент затухания:

Собственная частота:

Тогда резонансная частота:

Пример 14. Тело D массы mD = 10 кг расположено на гладкой плоскости, наклоненной под углом  = 30° к горизонту, и прикреплено к концу A пружины, коэффициент жесткости которой с = 36.1 Н / см (рис. 26). В некоторый момент к грузу D присоединяют груз Е массы mЕ = 15 кг. В тот же момент времени верхний конец пружины B начинает двигаться вдоль наклонной плоскости по закону
= 30° к горизонту, и прикреплено к концу A пружины, коэффициент жесткости которой с = 36.1 Н / см (рис. 26). В некоторый момент к грузу D присоединяют груз Е массы mЕ = 15 кг. В тот же момент времени верхний конец пружины B начинает двигаться вдоль наклонной плоскости по закону  см, причем точка O1 совпадает со средним положением точки B (при
см, причем точка O1 совпадает со средним положением точки B (при  ). Сопротивление движению двух грузов пропорционально их скорости v,
). Сопротивление движению двух грузов пропорционально их скорости v,  , где
, где 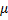 = 100 (Нс) /м – коэффициент сопротивления. Найти уравнение движения грузов D и E.
= 100 (Нс) /м – коэффициент сопротивления. Найти уравнение движения грузов D и E.

Рис.26
Решение. Направим оси Ox и  вдоль наклонной плоскости вниз, в сторону растяжения пружины (рис. 27). Начало O координатной оси Ox совместим с положением покоя грузов D и E, соответствующим статической деформации пружины, при условии, что точка B занимает свое среднее положение (
вдоль наклонной плоскости вниз, в сторону растяжения пружины (рис. 27). Начало O координатной оси Ox совместим с положением покоя грузов D и E, соответствующим статической деформации пружины, при условии, что точка B занимает свое среднее положение ( ). В этом положении пружина растянута на величину
). В этом положении пружина растянута на величину  , где
, где  и
и  – статические деформации пружины под действием груза D и E.
– статические деформации пружины под действием груза D и E.

Рис.27
Изобразим грузы в промежуточном положении, отстоящем от начала координат на величину x (точка M). Если бы верхний конец пружины был неподвижен, то в этом положении пружина была бы растянута на величину ( ). Но при смещении вниз верхнего конца пружины на некоторую величину
). Но при смещении вниз верхнего конца пружины на некоторую величину  удлинение пружины окажется меньшим на эту величину
удлинение пружины окажется меньшим на эту величину  , т.е.
, т.е. 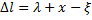 . Следовательно, проекция силы упругости пружины на ось x в точке M будет определяться выражением:
. Следовательно, проекция силы упругости пружины на ось x в точке M будет определяться выражением:  . Проекция силы сопротивления
. Проекция силы сопротивления  . Таким образом, дифференциальное уравнение движения грузов в проекции на ось x имеет вид
. Таким образом, дифференциальное уравнение движения грузов в проекции на ось x имеет вид
 ,
,
где  . Учитывая, что в состоянии статического равновесия грузов
. Учитывая, что в состоянии статического равновесия грузов  , получим
, получим
 ,
,
или
 , (1)
, (1)
где



Начальные условия для уравнения (1) определяются соотношениями

Как известно, решение линейного дифференциального уравнения (1) складывается из общего решения  соответствующего однородного уравнения
соответствующего однородного уравнения
 (2)
(2)
и частного решения x 2 неоднородного уравнения (1)
 . (3)
. (3)
Общее решение однородного уравнения (2) имеет вид
 . (4)
. (4)
Частное решение неоднородного уравнения (3) будем искать в виде
 . (5)
. (5)
Определив производные  подставив их в уравнение (3), получим
подставив их в уравнение (3), получим

Чтобы полученное равенство выполнялось в любой момент времени, необходимо равенство нулю выражений в квадратных скобках. Таким образом, для определения коэффициентов A1 и A2 имеем систему из двух линейных уравнений

решение которой записывается так

или после подстановки численных данных
А 1 = –0.7472 см, А 2 = –0.0034 см.
|

причем скорость точки равна


Постоянные интегрирования C1 и C2 определим из начальных условий: С 1 = –1.2928 см, С 2 = –0.2181 см. В результате уравнение движения груза имеет вид
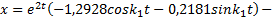

Вопросы для самопроверки
- Под действием какой силы совершаются свободные колебания материальной точки?
- Какой вид имеет дифференциальное уравнение свободных колебаний материальной точки?
- От каких факторов зависят частота, период, амплитуда и начальная фаза свободных колебаний материальной точки?
- Каков вид графиков свободных и затухающих колебаний, а также апериодического движения материальной точки?
- Какой вид имеет дифференциальное уравнение вынужденных колебаний материальной точки и каково его общее решение?
- Из каких составляющих движений складывается движение материальной точки, находящейся под действием восстанавливающей и возмущающей сил?
- Каковы частота и период вынужденных колебаний материальной точки?
- Какие вынужденные колебания называются колебаниями малой частоты и какие – колебаниями большой частоты? Чем характеризуется тот и другой вид колебаний?
- От каких факторов зависит амплитуда вынужденных колебаний точки?
- Что называют коэффициентом динамичности и каков график его зависимости от отношения p / k?
- При каком условии возникает явление биений? Каков график биений?
- При каких условиях возникает резонанс и каковы уравнения и график вынужденных колебаний материальной точки при резонансе?
- Как влияет сопротивление, пропорциональное скорости, на амплитуду, фазу, частоту и период вынужденных колебаний?
- Как определить максимальное значение амплитуды вынужденных колебаний при данном значении коэффициента затухания n?
- При каком значении коэффициента затухания максимум амплитуды вынужденных колебаний не существует?
- Какова зависимость сдвига фазы колебаний  от частоты изменения возмущающей силы p и от коэффициента затухания n?
от частоты изменения возмущающей силы p и от коэффициента затухания n?






