Если сила, которая вывела систему из положения равновесия, продолжает действовать, то такое колебание не будет свободным, будет вынужденным. И эта сила называется возмущающей силой.
Рассмотрим колебательное движение под действием обобщенной возмущающей силы, изменяющейся по гармоническому закону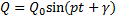 
, где 
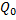- максимальная величина возмущающей силы; р – частота изменения силы; 
– начальная фаза изменения силы.
Дифференциальное уравнение вынужденных колебаний получится таким
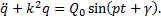(15)
Решение этого линейного неоднородного дифференциального уравнения состоит из общего решения соответствующего однородного уравнения и частного решения. Общее решение уже было получено в (7) или (8). Частное решение ищем в виде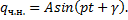 
Подставив его в дифференциальное уравнение (15), получим
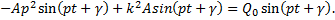Отсюда
Значит полное решение уравнения (15)
(17)
Так как общее и частное решения совершаются с разными частотами, то вынужденные колебания не будут гармоническими. Но, как нам уже известно, общее решение определяет свободные колебания, которые с течением времени довольно быстро затухают. Поэтому интерес представляют только установившиеся колебания:
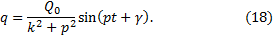
Отсюда следует, что установившиеся вынужденные колебания будут гармоническими с частотой р, равной частоте возмущающей силы и, что они не зависят от начальных условий.
И, самое интересное, – амплитуда колебаний А зависит от частоты р возмущающей силы. График этой зависимости дан на рис.7.
Рис.7
Первое, что надо отметить, при p = k (частота возмущающей силы равна частоте свободных колебаний) амплитуда увеличивается до бесконечности.
Это явление называется резонансом.
Как известно из курса высшей математики, при p = k решение (17) не будет удовлетворять уравнению (15). Частное решение надо искать в другом виде:
Подставив его в уравнение (15), получим:
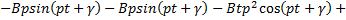
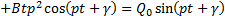
Отсюда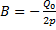 
и частное решение, определяющее вынужденные колебания при резонансе, получится таким
Видим, что амплитуда колебаний беспредельно равномерно увеличивается (рис.8). Амплитуда не сразу становится бесконечно большой. И даже малая возмущающая сила может раскачать систему до больших амплитуд и вызвать разрушение конструкции.
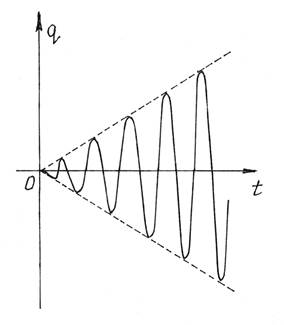
Рис.8
Интересен еще один случай, при котором частота р возмущающей силы близка к частоте свободных колебаний,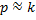 
, но не равна ей.
Воспользуемся решением (17), положив для простоты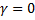 
. Пусть в начале движения координата и скорость равнялись нулю (при t = 0 q = 0 и 
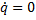). Подставим эти начальные условия в уравнения
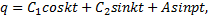
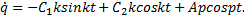
Получим два уравнения: 0=C1 и 0=C2k+Ap, из которых находим C1=0, C2=-Ap/k. Тогда уравнение колебаний 
Так как 
и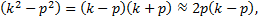 
то, по (16),
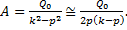
Кроме того 
Уравнение движения получится таким
(20)
Рассматривая функцию, стоящую перед cospt, как амплитуду колебаний, замечаем, что она изменяется по гармоническому закону с периодом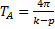 
от нуля до максимального значения 
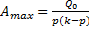(рис.9).
Сами колебания совершаются с частотой р и периодом 
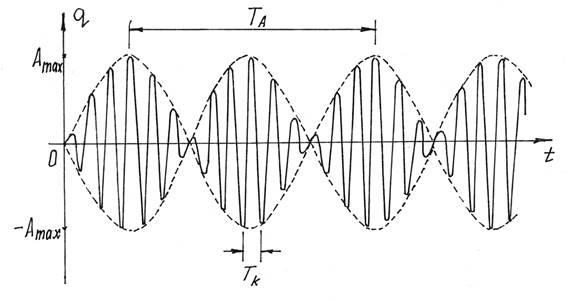
Рис.9
Чем ближе частота возмущающей силы р к частоте k, т.е. чем ближе к резонансу, тем больше будет период амплитуды TA и больше амплитуда Amax. И тем больше будет похож график на рис.9 на график на рис.8, изображающий колебания при резонансе. Эти колебания с периодически изменяющейся амплитудой называются биениями. Такое явление часто встречается, например, в радиотехнике.
Мы исследовали вынужденные колебания под действием возмущающей силы, изменяющейся по гармоническому закону. Но нередко она оказывается более сложной. Приходится использовать специальные математические методы, чтобы получить более-менее точный результат.
Если возмущающая сила периодическая и ее можно разложить в ряд Фурье, то решение может оказаться не очень сложным.
Пусть возмущающая сила описывается периодической функцией Q = Q (t) с периодом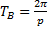 
, р – частота изменения этой функции. И пусть конструкция ее позволяет разложить функцию в ряд Фурье:
где Qj и 
- коэффициенты Фурье, определяемые по специальным формулам.
Частное решение дифференциального уравнения (15) получится в виде ряда:
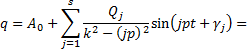
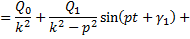
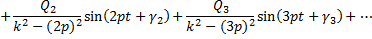
Количество s членов этого ряда стараются иметь не очень большим, если ряд хорошо сходится.
Решение получается как сумма нескольких синусоид («гармоник») с кратными частотами. Наименьшая частота р – называется основной частотой.
Интересно, что в полученном решении возможно несколько резонансов, столько, сколько гармоник: при p = k, p=k/2, p=k/3 и т.д.
