Цель: отработать навыки решения дифференциальных уравнений первого и
второго порядка.
Форма работы: решение задач.
Задания для самостоятельной работы:
1. Решить дифференциальные уравнения первого порядка с разделяющимися переменными:
;
;
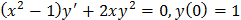2. Решить линейные дифференциальные уравнения первого порядка:
;
3.Решить дифференциальное уравнение второго порядка:
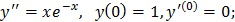
Список рекомендуемой литературы:
Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki
1. БогомоловН.В., СамойленкоО.Н.Математика//Учебник для техникумов.- М.: Наука, 2004.
2. Данко П.Е., Попов А.Г., Коженикова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. – М.: Высшая школа, 1999.
3. ПехлецкийИ.Д..Математика//Учебник для техникумов.- М.: Наука, 2001.
Порядок проверки, защиты самостоятельной работы:
проверка рабочей тетради
Тема 2.1 Элементы теории погрешностей
Цель: выработка умений и навыков по нахождению и обработке информации.
Форма работы: изучение основной и дополнительной литературы
Задания для самостоятельной работы.
Подготовить сообщение: «История возникновения теории ошибок»
Список рекомендуемой литературы:
Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki
4. БогомоловН.В., СамойленкоО.Н.Математика//Учебник для техникумов.- М.: Наука, 2004.
5. Данко П.Е., Попов А.Г., Коженикова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. – М.: Высшая школа, 1999.
6. ПехлецкийИ.Д..Математика//Учебник для техникумов.- М.: Наука, 2001.
7. www.sheynin.de/download/Istoria_Teorii_Oshibok.pdf
Порядок проверки, защиты самостоятельной работы:
проверка рабочей тетради
Тема 2.2 Численное интегрирование
Цель: выработка умений и навыков по решению задач.
Форма работы: изучение основной и дополнительной литературы, решение задач.
Задания для самостоятельной работы.
1. Вычислить 
методом прямоугольников, разделив промежуток [0, π] на 10 равных частей. Найти точное значение интеграла по формуле Ньютона – Лейбница и относительную погрешность приближенного вычисления.
2. Вычислить по формуле трапеций интеграл и сравнить с результатом предыдущей задачи.
3. Вычислить по формуле Симпсона интеграл 
Список рекомендуемой литературы:
Википедия – свободная энциклопедия http://ru.wikipedia.org/wiki
8. БогомоловН.В., СамойленкоО.Н.Математика//Учебник для техникумов.- М.: Наука, 2004.
9. Данко П.Е., Попов А.Г., Коженикова Т.Я. Высшая математика в упражнениях и задачах. Часть 2. – М.: Высшая школа, 1999.
10. ПехлецкийИ.Д..Математика//Учебник для техникумов.- М.: Наука, 2001.
Порядок проверки, защиты самостоятельной работы:
проверка рабочей тетради
