Цель работы: 1) изучить экспериментальные методы определения угла смачивания, 2) изучить влияние ПАВ на угол смачивания
Краткое теоретическое введение
В гетерогенных системах, содержащих жидкость, в микроскопическом масштабе наблюдаются явления, которые связаны с существованием механических сил, действующих в поверхностных слоях жидкости. Существование таких сил становится наиболее очевидным, если рассмотреть опыт, схематически представленный на рис. 6.1. В петлю из химически инертной металлической проволоки с подвижной перемычкой помещена капля жидкости, например мыльного раствора. Если перемычку слегка потянуть в сторону увеличения площади петли, капля растянется до тонкой плёнки. Чтобы поддерживать плёнку в растянутом виде, нужна сила F, пропорциональная длине перемычки L, что свидетельствует о некоторой упругости плёнки. По третьему закону Ньютона, внешняя сила F должна быть уравновешена противоположно направленной силой, действующей в плоскости плёнки и так же пропорциональной длине перемычки L. Обозначив эту силу в расчете на единицу длины s, можно записать:
F = – s×L (6.1)
Тот же опыт можно рассмотреть иначе. Представим бесконечно малое перемещение перемычки из положения равновесия d x. Очевидно, при этом совершается работа:
d W = – F ×d x = s×L ×d x
Поскольку произведение L ×d x равно изменению площади плёнки d S, это уравнение можно переписать:
d W = s ×d S (6.2)
Таким образом, одну и ту же величину s можно определить как силу в расчете на единицу длины, с основной единицей измерения Н/м, и как работу образования единицы площади плёнки, с основной единицей измерения Дж/м2.
Рассматриваемая величина s по физическому смыслу аналогична механическому напряжению, которое возникает в упругом теле при действии на него деформирующей силы. Когда речь идёт о поверхности раздела жидкость/газ, эта величина называется поверхностным натяжением. Когда речь идёт о поверхности раздела жидкость/жидкость или жидкость/твёрдое, её обычно называют межфазным натяжением. По определению, поверхностное натяжение жидкости – это сила, действующая в поверхностном слое тангенциально (или по касательной) к поверхности, и отнесённая к единице длины. В отсутствии внешних сил, поверхностное натяжение стягивает поверхность жидкости и заставляет её (жидкость) принимать шарообразную форму. Например, очень маленькая капля жидкости в воздухе или в объёме другой жидкости (которая не смешивается с первой) имеет форму шара. Более крупные капли или большие объёмы жидкости деформируются и принимают другую форму под действием силы тяжести.
Стремление малой капли иметь сферическую форму удобно объяснять, рассматривая s как работу образования единицы площади поверхности раздела фаз. Сфера – геометрическое тело, которое при данном объёме имеет минимальную площадь поверхности. Поэтому при образовании сферической капли система совершает минимальную возможную работу. Аналогичное объяснение можно дать из соображений термодинамической устойчивости. Свободная энергия обратимого процесса равна
, (6.3)
где Sэ – энтропия системы, W – другие виды работы, совершаемой системой, кроме механической работы изменения объёма V; остальные символы имеют обычное значение. В однокомпонентной системе, образование (плоской) поверхности раздела фаз связано с единственным видом работы (6.2), так что
, (6.3a)
откуда следует, что при постоянных T и V величина s представляет удельную свободную поверхностную энергию:
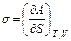, (6.4)
избыточную по отношению к гипотетической равновесной системе с теми же Sэ, P, V, и T, но без поверхности раздела фаз. Поскольку при равновесии система должна иметь минимальную свободную энергию, площадь поверхности раздела фаз должна быть минимальной. Из этого следует, что форма капли должна быть сферической. (В многокомпонентной системе, работа образования поверхности раздела включает также химическую составляющую, связанную с адсорбцией, из-за чего удельная поверхностная энергия не равна s. Это, однако, не меняет вывода о том, что при равновесии, в отсутствии гравитационного поля, капля должна иметь форму с минимальной площадью поверхности).
В системах жидкость/газ/твёрдое и жидкость/жидкость/твёрдое капля жидкости может иметь другую форму. Если очень маленькая капля нанесена на плоскую гладкую поверхность твёрдого тела, она, как правило, образует сферический сегмент, ограниченный снизу твёрдой поверхностью (рис. 6.2). В зависимости от свойств трёх контактирующих фаз, форма сегмента отвечает большему или меньшему растеканию капли по твёрдой поверхности. Окружность в основании сегмента, вдоль которой соприкасаются все три фазы, называется линией смачивания. Степень растекания капли характеризуется так называемым краевым углом или углом смачивания q – углом между касательной, проведённой к поверхности сегмента через любую точку линии смачивания, и твёрдой поверхностью, причем этот угол отсчитывается в сторону жидкой фазы. В отношении этого угла принято различать три случая
1) если 90°< q < 180° (рис. 6.2 а), жидкость называют несмачивающей по отношению к данной поверхности, а поверхность называют лиофобной по отношению к жидкости. Если жидкость – вода, то поверхность называют гидрофобной. Примеры: капля воды на поверхности полипропилена, фторопласта или парафина, капля ртути на поверхности чистого стекла.
2) если 0°< q < 90° (рис. 6.2 б), жидкость называют ограниченно смачивающей по отношению к данной поверхности, а поверхность называют лиофильной по отношению к жидкости (гидрофильной, если жидкость - вода). Пример: вода на поверхности стали и многих других металлов.
3) если q = 0°, то есть жидкость полностью растекается, её называют полностью смачивающей. Примеры: ртуть на свинце, вода на свеже полученном оконном стекле (обычное стекло, поверхность которого выщелачена, смачивается водой ограниченно). Полное смачивание является следствием химической нестойкости твёрдого тела по отношению к жидкости (например, стекла по отношению к воде) или следсвтием образования твёрдого раствора (например, растворение ртути в поверхностном слое свинца с образованием амальгамы).
Угол смачивания определяется величинами межфазного натяжения на границах пар каждой из трёх фаз: s тж, s тг, и s жг, где индексы т, ж, и г обозначают твёрдую, жидкую и газообразную фазу, соответственно. Представим, что капля на рис. 6.2 увеличивает площадь основания сегмента на бесконечно малую величину d S. При этом поверхностная энергия раздела твёрдое/газ уменьшается на величину s тг×d S, поверхностная энергия раздела твёрдое/жидкость увеличивается на величину s тж×d S, поверхностная энергия раздела жидкость/газ увеличивается на величину s жг×d S жг, где изменение площади d S жгпредставляет проекцию изменения площади основания d S на поверхность жидкость/газ, то есть d S жг= d S ×cos q ·. Суммарное изменение свободной энергии при T и V = const составляет
d А = – s тг×d S + s тж×d S + s жг×d S ×cos q (6.5)
При бесконечно малом отклонении от равновесия d А = 0. Поэтому из (6.5), после сокращения d S, следует соотношение, известное как уравнение Юнга:
s тж– s тг+ s жг×cos q = 0 (6.6)
или:
(6.6а)
Практическое применение этого уравнения ограничено, так как межфазное натяжение на границе твёрдых тел с другими фазами не может быть измерено экспериментально прямыми методами. Тем не менее, оно позволяет делать некоторые важные выводы о смачивании. Например, предположим, что сравнивается смачивание некоторого твёрдого тела водой и водным раствором дифильного ПАВ. Дифильные ПАВ, как известно, адсорбируются и снижают межфазное натяжение на любых поверхностях раздела фаз (см. лаб. работу 3). Поэтому при добавлении ПАВ к воде s жгуменьшается и уменьшается знаменатель дроби в правой части (6.6а). Величина s тжтак же уменьшается, а s тгостаётся постоянной (при условии, что ПАВ нелетуч и не может адсорбироваться на границе твёрдое/газ). То есть, числитель в (6.6а) увеличивается, что вместе с уменьшением знаменателя должно вести к увеличению cos q и уменьшению q (поскольку косинус – убывающая функция в области q от 0 до 180°). Таким образом, из уравнения Юнга следует, что добавление ПАВ к воде должно увеличивать смачивание любых твёрдых поверхностей.
Другое полезное термодинамическое соотношение касается работы адгезии жидкости к поверхности твёрдого тела (adhesion - прилипание). Представим, что при постоянных T и V сферический сегмент жидкости на рис. 6.2 отделяется от твёрдой поверхности без изменения его формы. При этом поверхностная энергия раздела твёрдое/газ увеличивается на величину s тг× S, где S – площадь основания сегмента; поверхностная энергия раздела твёрдое/жидкость уменьшается на величину s тж× S (эта поверхность раздела просто исчезает), поверхностная энергия раздела жидкость/газ увеличивается на величину s жг× S, так что полная работа (в отсутствии адсорбции) составляет
W = s тг ×S - s тж ×S + s жг ×S
В расчёте на единицу площади получается уравнение
w = s тг - s тж + s жг(6.7)
называемое уравнение Дюпре. В комбинации с уравнением Юнга (6.6) работу адгезии можно выразить через угол смачивания:
w = s жг(1 + cos q) (6.7а)
Из этой формы записи видно, что чем меньше угол смачивания и чем больше поверхностное натяжение жидкости, тем больше работа адгезии капли.
Смачивание можно наблюдать не только при нанесении маленькой капли на твёрдую поверхность, но и при любом контакте жидкости с твёрдой поверхностью, когда угол между свободной поверхностью жидкости и поверхностью твёрдого тела отличается от равновесного угла смачивания. Например, если жидкость находится в сосуде с вертикальными стенками, то её свободная поверхность является плоской и горизонтальной, из-за действия силы тяжести. При внимательном наблюдении (особенно с помощью увеличительного стекла) можно заметить, что в месте контакта со стенками сосуда поверхность жидкости искривлена. Такой искривлённый участок называется мениском жидкости. Наиболее удобно его наблюдать, когда жидкость находится внутри капилляра – в узкой трубке с диаметром менее приблизительно 0.5 мм (иногда капилляром называют даже более широкие трубки, однако следует обратить внимание на определение константы капиллярности, данное ниже). Предположим, капиллярная трубка, открытая с обоих концов, погружена одним концом в жидкость. Внутри капилляра жидкость образует мениск (рис. 6.3). Угол между касательной, проведённой к поверхности мениска через любую точку линии смачивания, и поверхностью капилляра, отсчитанный в сторону жидкости – это угол смачивания q, который мог бы наблюдаться в той же системе жидкость/твёрдое/газ, если бы твёрдая поверхность была плоской и горизонтальной, а жидкость была маленькой каплей (рис. 6.2).
Искривление поверхности жидкости внутри капилляра является причиной поднятия или опускания столба жидкости выше или ниже, соответственно, уровня плоской поверхности (за пределами капилляра). Согласно закону Лапласа, давление под сферической поверхностью жидкости отличается от давления в газовой фазе над поверхностью жидкости на величину:
D Р = Р газ – Р ж = 2s/R
где R – радиус кривизны сегмента (он равен радиусу сферы, до которой достраивается сферический сегмент). Если мениск выпуклый в сторону жидкости, то радиус кривизны отрицательный, D Р < 0 и столб жидкости в капилляре поднимается выше уровня плоской поверхности жидкости (рис. 6.3 б). Если мениск выпуклый в сторону газа, то радиус кривизны положительный, D Р > 0 и столб жидкости в капилляре остаётся ниже уровня плоской поверхности жидкости (рис. 6.3 а). Высота h мениска над или под плоской поверхностью может быть найдена из равенства перепада давления D Р капиллярному давлению – то есть избытку (или недостатку) гидростатического давления столба жидкости (r ж- r г) hg по сравнению с жидкостью за пределами капилляра:
2 s/R = (r ж- r г) hg
откуда следует 
Как можно вывести из геометрического рассмотрения, радиус кривизны шарового сегмента связан с радиусом капилляра r соотношением R = r /cos q. Поэтому последнее уравнение можно переписать в виде:
(6.8)
В такой записи это уравнение известно как уравнение Жюрена. Из него следует, что если q > 90° (cos q < 0), то h < 0 (рис. 6.3 а). Если q < 90° (cos q > 0), то h > 0 (рис. 6.3 б).
Формулу Жюрена часто представляют в ви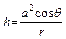де 
, где 
называется капиллярной постоянной или константой капиллярности. Эта константа имеет размерность длины и характеризует относительную способность жидкости к капиллярным явлениям, например к поднятию или опусканию столба жидкости в капилляре. Иначе можно сказать, что она характеризует радиус капилляра, при котором данная жидкость начинает проявлять капиллярные свойства. Например, для воды а = 0.38 мм при 20 °С. Это значит, что в случае воды, капиллярные явления становятся заметны при радиусах капилляра менее 0.38 мм.
Приборы и методы измерений
Методы определения угла смачивания основаны на получении увеличенного изображения зоны контакта между тремя фазами и геометрического анализа этой зоны. Одним из наиболее точных является метод наклонной пластинки. Из исследуемого твёрдого материала изготавливают плоскопараллельную пластину с гладкими плоскими поверхностями, погружают её в испытуемую жидкость (или в контактирующие жидкости), и с помощью оптического прибора наблюдают форму поверхности раздела жидкость/газ (или жидкость/жидкость), примыкающей к поверхности пластины. В общем случае, эта поверхность искривлена. Пластину наклоняют (относительно вертикали) до такого положения, при котором искривление поверхности раздела ж/г (или ж/ж) исчезает полностью, так что эта поверхность становится плоской вплоть до поверхности пластины (рис. 6.4). Угол между пластиной в таком положении и горизонтальной поверхностью раздела ж/г (или ж/ж) равен углу смачивания. Преимущество этого метода в том, что с помощью подходящих механических и оптических аксессуаров угол наклона пластины может быть измерен и отрегулирован с очень большой точностью.
Менее точным, но более распространённым является метод "сидячей" капли, при котором каплю испытуемой жидкости наносят на гладкую плоскую поверхность твёрдого материала и анализируют увеличенное изображения её силуэта. Есть два основных варианта анализа: 1) прямое измерение и 2) геометрический анализ шарового сегмента. В первом способе находят положение касательной к поверхности сегмента и определяют её угол наклона. Во втором способе измеряют высоту сегмента h (в геометрии её иногда называют стрелкой сегмента), и радиус основания сегмента х (рис. 6.5). Если форма капли соответствует шаровому сегменту в точности, угол смачивания может быть найден из соотношения:
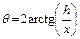(6.9)
Геометрические параметры h и х могут быть измерены с большой точностью, в связи с чем считается, что этот метод анализа имеет преимущество перед прямым методом нахождения касательной. К сожалению, реальные капли, как правило, более или менее деформированы из-за действия силы тяжести. Деформация приводит к заниженным значениям высоты (рис. 6.5). Степень деформации зависит от размера капли и капиллярной постоянной жидкости. Большие капли с малой константой капиллярности наиболее подвержены деформации. Обычно, формула (6.9) даёт достаточно точные результаты при размере капель менее 1.5 мм. Однако такие малые капли довольно быстро испаряются, что является другим источником занижения h. Чтобы предотвратить испарение, необходимо обеспечить равновесное давление паров жидкости в пространстве вокруг капли, но это представляет сложную техническую проблему в данном методе. В качестве альтернативы, анализируют капли большего размера (2-3 мм) и вводят поправки на деформацию, которые зависят от константы капиллярности и наблюдаемой высоты h.
В настоящей работе используется метод сидячей капли с прямым измерением угла смачивания. Хотя измерение угла наклона касательной является менее точным, чем измерение параметров h и х, этот угол менее чувствителен к деформации больших капель, чем высота h. Благодаря этому, можно использовать сравнительно большие капли (до 3 мм) без применения поправок на деформацию.
Каплю жидкости, размером ~2 мм, наносят с помощью шприца на чистую гладкую поверхность твёрдого вещества в виде пластины, которая установлена на подвижную подставку между источником света и объективом проектора. На экране проектора появляется увеличенное перевёрнутое изображение капли (АВС на рис. 6.6) и её отражения (АDC) в плоскости пластины. Граница раздела пластина/воздух и пластина/капля при таком изображении почти не различима. Однако её можно определить как прямую, соединяющую точки А и С в местах, где соединяются дуги АВС и АDC. Изображение капли, включая точки А и С фотографируют или копируют иным способом на лист бумаги, проводят прямую через точки А и С и продолжают несколько дугу АВС (штриховые линии на рис. 6.6), как продолжение сегмента сферы, для более удобного построения касательных. Через точки А и С проводят касательные и находят углы между ними и линией АС, отсчитываемые в сторону жидкости.
Последовательность выполнения работы
В настоящей работе исследуются три твёрдых материала в виде пластин: пластмасса (фторопласт), металл (нержавеющая сталь) и стекло. Исследуемыми жидкостями являются вода и водные растворы олеата натрия. Концентрации олеата натрия могут быть выбраны такие же, как в работе № 5. (См. приготовление растворов в работе 5). Достаточно приготовить очень небольшие объёмы растворов. Например, 5 мл каждого раствора достаточно с избытком в данной работе.
Пластины из твёрдых материалов моют обильно водопроводной водой и затем ополаскивают дистиллированной водой. После этого протирают их ватой или фильтровальной бумагой и в дальнейшем избегают загрязнения рабочих поверхностей (в частности, избегают касания их руками).
Рекомендуется начинать измерения с дистиллированной воды в порядке пластмасса-металл-стекло, повторяя затем измерения на каждом из этих материалов (в том же порядке) с очередной более высокой концентрацией олеата натрия. При таком проведении измерений можно использовать один шприц, который следует промыть водой только в заключении измерений. Испытуемые пластины при переходе от одной концентрации к другой достаточно промокнуть насухо фильтровальной бумагой и по окончанию экспериментов промыть водопроводной и дистиллированной водой.
Очередную пластину устанавливают на деревянную подставку между источником света и объективом проектора и наносят на неё каплю очередного раствора из шприца. Следует стремиться к получению малых капель, не более 2 мм. Включают освещение прибора (и, если в этом есть необходимость, выключают общее освещение в помещении). Наблюдая за изображением капли на экране, регулируют положение пластины (вместе с подставкой) до наиболее резкого изображения капли. Затем на экран проектора накладывают полупрозрачную бумагу и копируют изображение карандашом. Следует по возможности точно копировать то, что является существенным для определения q, а именно – положение точек А и С, указывающих положение поверхности пластины, и те участки дуги АВС, которые примыкают к этим точкам. Можно заранее нанести на лист бумаги прямую линию (с помощью линейки) и положить лист на экран проектора так, чтобы эта линия проходила через точки А и С, после чего скопировать участки дуги АВС, примыкающие к этим точкам, или всю дугу АВС. После получения копии освещение в проекторе следует выключить во избежание нагревания прибора. Процедуру повторяют на каждой из трёх пластин и с каждым из растворов. При наличии навыков достаточно двух измерений с одной каплей (углы q1 и q2 на рис. 6.6) для каждого раствора. Однако для приобретения необходимых навыков следует сделать две серии определений (по две капли и четыре измерения q) с первой жидкостью – водой на всех трёх пластинах.
Обработка и оформление результатов
1. На каждом из полученных изображений продолжают дугу АВС за пределы линии поверхности пластины, как показано штриховыми линиями на рис. 6.6, имея в виду, что скопированная дуга является дугой окружности. К точкам А и С на полученных дугах проводят касательные по одному из методов, описанных в приложении 2.2. Затем измеряют углы наклона касательных с помощью транспортира или вычисляют их из тригонометрических соотношений. Для вычисления можно построить любой прямоугольный треугольник с гипотенузой, лежащей на касательной. Измерить противолежащий катет а и прилежащий катет b (противолежащий и прилежащий по отношению к углу смачивания), и вычислить q = arctg(a/b). Можно использовать другие соотношения в треугольнике, однако в любом случае следует помнить, что точность такого вычисления существенно зависит от размера построенного треугольника – чем меньше треугольник, тем меньше точность.
2. Найденные углы смачивания занести в таблицу (см. табл. 6.1) и усреднить для каждого раствора на каждой пластине.
3. Вычислить работу адгезии каждого раствора по уравнению (6.7а). Для этого вычислить косинусы углов и использовать значения поверхностного натяжения, найденные сталагмометрическим методом в работе 5 для соответствующих концентраций.
4. Построить три кривые (для трёх материалов пластин) зависимости cos q от концентрации ПАВ.
5. Сделать выводы о свойствах трёх материалов в отношении смачивания водой и о влиянии ПАВ на смачивание.
Контрольные вопросы
1. Что называется поверхностным натяжением?
2. Как объяснить, почему маленькие капли жидкости стремятся принять форму шара?
3. Сформулируйте по возможности точно, что называется углом смачивания.
4. Как классифицируются жидкости по отношению к данной твёрдой поверхности с точки зрения смачивания? Как классифицируются твёрдые материалы по отношению к смачиванию данной жидкостью?
5. Как и почему влияют ПАВ на смачивание твёрдых тел водными растворами?
6. Что называется работой адгезии и от чего она зависит?
7. Что называется капилляром? Чем капилляры отличаются от обычных трубок?
8. Объясните, почему уровень столба жидкости внутри капилляра обычно бывает выше или ниже уровня свободной поверхности жидкости?
9. Какие экспериментальные методы применяются для определения угла смачивания гладких твердых поверхностей?
10. Чем неудобны малые капли и чем плохи большие капли при определении угла смачивания?
11. Какие геометрические построения делаются при определении угла смачивания методом сидячей капли?
12. Перечислите основные стадии проведения экспериментальной работы. Что предстоит сделать сначала, что потом и т.д.?
13. Как может влиять мицеллообразование на зависимость угла смачивания от концентрации олеата натрия?
Литература
Зимон А.Д., Балакирев А.А., Дехтяренко Н.Г., Бабак В.Г., Аксёнов В.Н. Коллоидная химия. Лабораторный практикум. Часть 1. М: ВЗИПП 1986, Лаб. работа 6.
Адамсон А. Физическая химия поверхностей. (пер. с англ.) М: Мир 1979, Глава 7.
Surface and colloid science. Vol. 2 (Ed. E. Matijevic) N.Y. etc.: J. Wiley & Sons, 1969, Chapter 2.
Surface and colloid science. Vol. 11 (Ed. E. Matijevic) N.Y. etc.: J. Wiley & Sons, 1979, Chapter 2.
Рис. 6.1 Плёнка жидкости в петле с подвижной перемычкой.
Рис. 6.2 Форма очень маленькой капли на твёрдой поверхности. (а) несмачивание поверхности, (б) ограниченное смачивание
Рис. 6.3 Мениск жидкости в капилляре и капиллярное поднятие жидкости. (а) несмачивание капилляра, (б) ограниченное смачивание капилляра.
Рис. 6.4 Принципиальная схема метода наклонной пластинки
Рис. 6.5 Измерения в методе шарового сегмента. Непрерывной линией показана форма, не подверженная деформации силой тяжести. Пунктирной линией показана форма деформированной капли.
Рис. 6.6 Изображение капли в проекторе (жирные линии) и дополнительные построения (тонкие и штриховые линии), используемые для определения угла смачивания.
· при бесконечно малом увеличении основания шарового сегмента происходит также изменение угла смачивания dq. Однако можно показать (это требует дополнительных математических выкладок), что изменение cos(q + dq) имеет второй порядок малости по сравнению с dq, поэтому им можно пренебречь.
