Цель работы: Определение критической концентрации мицеллообразования по зависимости поверхностного натяжения растворов ПАВ от концентрации.
Краткое теоретическое введение
Наиболее эффективные поверхностно-активные вещества (ПАВ) имеют дифильное строение молекул. Этот термин означает, что часть молекулы имеет высокое сродство к воде и другим полярным растворителям, то есть является гидрофильной, тогда как другая часть той же молекулы имеет высокое сродство к неполярным растворителям и является липофильной. По отношению к воде липофильность эквивалентна гидрофобности. Гидрофобной частью является углеводородный радикал, который должен включать от 8 до 20 атомов углерода чтобы молекула имела действительно высокую поверхностную активность. Гидрофильной частью является полярная группа, способная диссоциировать на ионы в случае ионогенных ПАВ или неспособная диссоциировать в случае неионогенных ПАВ. Часто под термином ПАВ подразумеваются вещества именно с таким строением, хотя более общее определение ПАВ – это вещества, снижающие поверхностное натяжение раствора независимо от того, какое они имеют строение и сколько атомов углерода содержат в цепи.
Дифильное строение молекул является причиной ряда уникальных свойств. ПАВ легко адсорбируются на любых поверхностях раздела фаз. При этом гидрофильные части молекул ориентируются в сторону более полярной фазы, а гидрофобные цепи располагаются в неполярной фазе. Адсорбция обычно является обратимой и поэтому может быть охарактеризована химическим равновесием. Обозначив молекулу ПАВ символом A и молекулу растворителя – воды W, равновесие адсорбции можно записать в виде:
A + W(адсорб.) 
A(адсорб.) + W (5.1)
где (адсорб.) означает нахождение молекулы в адсорбционном слое.
В объёме раствора, независимо от присутствия или отсутствия поверхностей раздела фаз, молекулы ПАВ находятся в виде отдельных молекул (то есть в молекулярно-дисперсном состоянии), но могут также объединяться между собой с образованием коллоидных частиц, находящихся в равновесии с молекулярно-дисперсным ПАВ. Такие частицы принято называть мицеллами. При невысокой ионной силе водного раствора мицеллы имеют шарообразную форму и состоят из молекул ПАВ, гидрофильные группы которых находятся на поверхности мицеллы и контактируют с растворителем, а гидрофобные цепи ориентированы внутрь мицеллы и образуют её ядро, изолированное гидрофильной поверхностью от воды (см. рис. 7.2 и 7.3). В отсутствии других липофильных компонент размер мицелл определяется длиной углеводородного радикала, и для данного ПАВ может колебаться в сравнительно небольших пределах. У большинства ПАВ средний радиус сферических мицелл составляет от 1 до 10 нм. Число молекул ПАВ, образующих мицеллу, принято называть числом агрегации мицеллы. Это число определяется необходимостью образовать замкнутую сферу, поверхность которой состоит только из гидрофильных групп. В большинстве случаев оно составляет 50 – 100.
Движущей силой мицеллообразования являются так называемые гидрофобные взаимодействия, которые проявляются при растворении ПАВ в полярных растворителях. В частности, в воде молекулы растворителя взаимодействуют между собой с помощью водородных связей. Появление в воде протяжённых углеводородных радикалов приводит к нарушению кооперативного водородного связывания между молекулами растворителя, что является энергетически не выгодным, так как не компенсируется сольватацией углеводородных радикалов. Таким образом, в энергетическом отношении гидрофобные взаимодействия объясняются не столько взаимодействиями между углеводородными цепями в ядре мицеллы, сколько энергетической выгодностью взаимодействий молекул полярного растворителя между собой за пределами мицеллы. Аналогичным образом, при растворении ПАВ в неполярном растворителе можно говорить о гидрофильных взаимодействиях, суть которых состоит в энергетической невыгодности контактов гидрофильных групп ПАВ с молекулами неполярного растворителя. Результатом этого является образование так называемых обратных мицелл, ядро которых образовано гидрофильными группами молекул ПАВ и другими полярными молекулами (если они присутствует), а внешняя поверхность – липофильными углеводородными цепями.
Мицеллообразование зависит от концентрации ПАВ в растворе. Для данного ПАВ, при данной температуре, существует определённая концентрация, ниже которой весь ПАВ находится в молекулярно-дисперсном состоянии, и выше которой образуются мицеллы, находящиеся в равновесии с молекулярно-дисперсным ПАВ. Эту концентрацию называют критической концентрацией мицеллообразования (ККМ). Поскольку размер мицелл превышает 1 нм, растворы ПАВ с концентрацией выше ККМ являются коллоидными. Их принято относить к классу лиофильных коллоидов, то есть таких, которые образуются самопроизвольно и являются термодинамически равновесными.
Существуют две теории мицеллообразования. В одной из них, называемой псевдофазной теорией, мицеллы рассматриваются как частицы отдельной фазы, которые, несмотря на очень высокую дисперсность, являются термодинамически стабильными благодаря очень низкому межфазному натяжению на границе раздела мицелла/раствор. Мицеллообразование рассматривается как образование новой фазы, тогда как ККМ рассматривается как растворимость этой фазы. При концентрации ниже ККМ растворы являются ненасыщенными; при концентрации равной ККМ они являются насыщенным, а при концентрации выше ККМ они представляет собой гетерогенную систему, состоящую из насыщенного раствора с концентрацией молекулярно-дисперсного ПАВ равной ККМ и коллоидных частиц другой фазы, включающей весь ПАВ избыточный по отношению к ККМ.
В альтернативной теории, которую иногда называют квазихимической, растворы ПАВ рассматриваются как гомогенные, а мицеллообразование объясняется равновесием вида
nA An (5.2)
где An - мицелла с числом агрегации n.
Равновесия такого типа известны в химии как реакции ассоциации. (По этой причине коллоидные ПАВ называют также "ассоциативными коллоидами"). Хорошо известным примером является ассоциация уксусной кислоты
2СH3COOH (СH3COOH)2 (5.3)
которая происходит благодаря образованию сильных водородных связей между гидроксильной группой С–ОН одной молекулы и окси-группой С=О другой. Однако большинство таких реакций характеризуются числом агрегации 2, в отличие от мицеллообразования, при котором n = 50-100.
Чтобы понять как эта теория объясняет существование ККМ, необходимо рассмотреть математический аспект равновесия (5.2). В пренебрежении коэффициентами активности это равновесие можно описать константой:
, (5.4)
где скобки [ ] означают равновесную концентрацию в молярной шкале. Если весь ПАВ находится в виде либо молекул А, либо мицелл An, общая аналитическая концентрация ПАВ в растворе, С, равна сумме
С = [ A ] + n [ An ] (5.5)
Удобно рассматривать долю общей концентрации ПАВ, приходящуюся на мицеллы:
x = n [ An ]/ С (5.6)
Тогда равновесные концентрации можно записать в виде
[ An ] = xС / n, и [ A ] = (1– x) C
откуда следует
(5.7)
Это уравнение невозможно решить аналитически относительно x из-за высокой степени n, однако его можно решить относительно С:
(5.8)
и вычислить С для любого значения x. Рис. 5.1 а) показывает результаты вычислений для n = 2 и 100 при некоторых произвольных константах равновесия. Рис. 5.1 б) показывает те же результаты в области низких концентраций. Можно видеть, что при n = 2 доля молекул А в составе димеров А2 возрастает с ростом общей концентрации постепенно, без видимых особенностей на кривой. При n = 100, агрегированные частицы А100 практически отсутствуют при концентрациях менее ~ 0.09 ммоль/л (9×10–5 моль/л), но появляются и быстро увеличиваются по своему содержанию в узком интервале концентраций, прилегающем к 0.09 ммоль/л. Соответственно, доля 1– x молекулярно-дисперсного вещества А равна практически 1 при низких концентрациях, но уменьшается при С > ~ 0.09 ммоль/л, так что его абсолютная концентрация остаётся практически постоянной (рис. 5.1 в). Эта критическая концентрация, 0.09 ммоль/л, представляет в данном случае "точку" ККМ.
Положение точки ККМ зависит от степени агрегации n и от константы равновесия К, тогда как сам факт существования ККМ, то есть узкого интервала концентраций, в пределах которого происходит быстрый рост доли x агрегированного вещества, является исключительно следствием большой величины n. При малых n, например n = 2 (рис. 5.1 а и б), критическая концентрация отсутствует. Из сопоставления кривых для n = 2 и 100 на рис. 5.1 ясно так же, что для существования хорошо определённого значения ККМ мицеллы должны быть более или менее монодисперсными, потому что широкое распределение чисел агрегации приведёт к плавному увеличению x в широком интервале концентраций.
Следует заметить, что равновесие мицеллообразования (5.2) принято характеризовать именно величиной ККМ, а не константой равновесия (5.4). Для этого есть две причины. Во-первых, ККМ может быть определена экспериментально без большого труда и со сравнительно высокой точностью, тогда как для константы равновесия К и чисел агрегации n возможны лишь грубые оценки. Во-вторых, использование константы К неудобно из-за математических трудностей при вычислениях равновесных концентраций, связанных с высокими степенями n в уравнениях (5.4, 5.7 и 5.8).
Для разных дифильных ПАВ величины ККМ находятся в диапазоне концентраций приблизительно от 10 до 0.1 ммоль/л (от 10–2 до 10–4 моль/л). Точное значение зависит от природы ПАВ и внешних условий. В частности, при данном виде гидрофильной группы, ККМ изменяется таким образом:
- уменьшается с увеличением длины углеводородного радикала;
- уменьшается с уменьшением радиуса противоиона в случае катионактивных ПАВ (например, ККМ бромида цетилтриметиламмония много меньше, чем ККМ фторида цетилтриметиламмония);
- слабо зависит от радиуса противоиона в случае анионактивных ПАВ, но заметно уменьшается с увеличением его заряда (например, додецилсульфат кальция имеет меньшую ККМ, чем та же соль натрия);
- уменьшается с увеличением ионной силы раствора в случае ионогенных ПАВ (например, при добавлении NaCl или аналогичной соли к раствору ПАВ).
ККМ уменьшается с уменьшением температуры, однако для каждого ПАВ мицеллообразование ограничено некоторым интервалом температур, ниже которого (в случае ионогенных ПАВ) или выше которого (в случае неионогенных ПАВ) раствор расслаивается на две макроскопические фазы. Одна из них является молекулярно-дисперсным раствором, не содержащим мицелл, а другая является твёрдой или жидкой фазой ПАВ.
Приборы и методы измерений
Экспериментальные методы определения ККМ основываются на изменении зависимости свойств раствора от концентрации вблизи ККМ. Например, если какое-либо свойство J описывается зависимостью ¦(С) в области С < ККМ, то в области С > ККМ оно должно описываться другой зависимостью, скажем J = j(С). Концентрация, при которой происходит наиболее очевидный переход от ¦(С) к j(С), рассматривается как ККМ. Некоторые примеры таких зависимостей собраны на рис. 5.2.
Прямым методом определения ККМ является измерение мутности раствора как функции концентрации (турбидиметрические или нефелометрические измерения). В области низких концентраций (С < ККМ) раствор является истинным, поэтому его мутность низкая и едва увеличивается с ростом концентрации. В области С > ККМ раствор является коллоидным, соответственно его мутность быстро растёт с увеличением концентрации в этой области. Если построить график зависимости мутности от концентрации С в интервале С охватывающем ККМ, то вблизи ККМ будет наблюдаться изменение хода этой зависимости.
Осмотическое давление так же может быть использовано для нахождения ККМ. Если выбрать такую полупроницаемую мембрану, через которую проходят молекулы ПАВ, но не проходят мицеллы, то давление по обоим сторонам мембраны будет одинаковым, потому что молекулярно-дисперсный ПАВ будет находится в равновесии (5.2) с мицеллами в обоих камерах осмометра. Если выбрать мембрану правильно – то есть такую, которая не пропускает ни мицеллы, ни молекулярно-дисперсный ПАВ, то осмотическое давление в камере с раствором ПАВ будет расти с ростом концентрации: быстро вплоть до ККМ, но медленно при более высоких концентрациях (см. рис. 5.2). Это объясняется тем, что мицеллы имеют много больший молекулярный вес, чем молекулярно-дисперсный ПАВ, в связи с чем они слабо влияют на осмотическое давление. Применение этого метода ограничено необходимостью работать с очень плотными мембранами, способными задерживать относительно небольшие по размерам молекулы ПАВ.
Более распространённым методом, в случае ионогенных ПАВ, являются кондуктометрические измерения (измерения электрической проводимости). Ионогенный молекулярно-дисперсный ПАВ обычно является сильным электролитом. Поэтому с ростом С в области С < ККМ удельная проводимость растёт, а эквивалентная проводимость уменьшается, последняя в соответствии с законом квадратного корня l = l¥– АÖС. В области С > ККМ, при увеличении концентрации удельная проводимость растёт значительно медленнее, а эквивалентная проводимость уменьшается много быстрее, чем в области С < ККМ. Для этого есть две причины. Во-первых, подвижность мицелл значительно меньше подвижности молекулярно дисперсных ионов. Во-вторых, ПАВ в составе мицелл является слабым электролитом, потому что значительная часть противоионов связана электростатическими силами в слое Штерна мицелл и при наложении внешнего электрического поля эти противоионы не могут перемещаться самостоятельно (см. рис. 7.2 в работе 7). Упрощенно можно сказать, что весь электрический ток переносится молекулярно-дисперсным ПАВ, тогда как мицеллярный ПАВ почти не участвует в переносе электричества. В результате, при С > ККМ проводимость в расчёте на единицу объёма раствора (удельная проводимость) почти не зависит от концентрации ПАВ, так как в этой области концентрация [ A ] постоянна (рис. 5.1 в), тогда как проводимость в расчёте на моль растворённого ПАВ (эквивалентная проводимость) уменьшается, потому что доля 1– x молекулярно-дисперсного ПАВ уменьшается.
Другим методом является потенциометрическое измерение активности противоионов с помощью ионоселективных электродов. Например, активность противоионов Na+ можно легко измерить с помощью Na+–селективного стеклянного электрода в комплекте с обычным рН-метром. Активность противоионов всегда увеличивается с увеличением концентрации ПАВ, однако в области С > ККМ наклон кривой оказывается меньше, из-за того что часть противоионов остаётся в слое Штерна мицелл. Этот метод получил широкое распространение в последние годы (вместе с распространением ионоселективных электродов) благодаря тому что он менее чувствителен к присутствию посторонних примесей, чем турбидиметрический или кондуктометрический методы.
В настоящей работе ККМ определяется по данным о зависимости поверхностного натяжения раствора от его концентрации. Поверхностное натяжение связано с адсорбцией G по известному уравнению Гиббса. В его простой записи (3.6а) оно справедливо для растворов, содержащих только один растворённый компонент, тогда как растворы дифильных ПАВ в общем случае содержат два растворённых компонента – молекулярно дисперсный ПАВ и мицеллы. По этой причине для поверхностного натяжения s необходимо использовать более общее уравнение 3.5а, которое в обозначениях настоящей работы может быть записано таким образом:
(5.9)
В области концентраций С < ККМ, концентрация мицелл 
равна нулю и [ A ] = С. С учётом этого из (5.9) получается следующая зависимость s от концентрации
, (5.10)
где s 0 – поверхностное натяжение чистого растворителя. Уравнения Гиббса и Лэнгмюра в этой области концентраций имеют вид
, 
где b – отношение константы равновесия (5.1) к концентрации растворителя (воды).
В области концентраций С ³ ККМ, концентрация молекулярно-дисперсного ПАВ приблизительно постоянна и равна ККМ, а концентрация мицелл составляет 
= С – ККМ. Поэтому член d ln [ A ] в уравнении (5.9) приблизительно равен нулю. Тогда из уравнения (5.9) следует:
(5.10а)
Таким образом, зависимость s от концентрации описывается разными уравнениями в областях концентраций С < ККМ и С ³ ККМ. Эти уравнения (5.10 и 5.10а) отличаются величинами адсорбции ГА и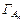 
. Молекулярно-дисперсный дифильный ПАВ имеет асимметричное химическое строение – гидрофильную группу атомов на одном конце молекулы и протяженный углеводородный радикал с другой стороны. Благодаря этому его адсорбция ГА велика и положительна. Поэтому в области С < ККМ следует ожидать сильное уменьшение s с увеличением концентрации. Мицеллы имеют симметричное химическое строение. Углеводородные цепи в них обращены внутрь ядер, а сферическая поверхность является гидрофильной. Из-за этого для них можно ожидать небольшую отрицательную или близкую к нулю адсорбцию 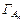. Следовательно, по уравнению (5.10а) можно ожидать приблизительное постоянство или небольшое увеличение s при увеличении концентрации выше точки ККМ.
Фактически, у большинства дифильных ПАВ s сильно уменьшается в области С < ККМ и продолжает уменьшаться в области С > ККМ, но в значительно меньшей степени, чем при С < ККМ (см. рис. 5.2). Вероятно, это объясняется тем, что концентрация молекулярно-дисперсного ПАВ не совсем постоянна в области С > ККМ. Тем не менее, ККМ может быть легко найдена из графика зависимости s от С как концентрация, при которой наблюдается переход от одной зависимости s от С к другой.
Для измерения поверхностного натяжения в настоящей работе применяется сталагмометрический метод. Сталагмометр представляет собой вертикальную капиллярную трубку, служащую для медленного контролируемого истечения жидкости в виде отдельных капель. Согласно уравнению Тейта (1863 г), вес капли (mg), отрывающейся от кончика трубки, пропорционален длине внешней окружности трубки 2p R и поверхностному натяжению s:
mg = 2p Rs (5.11)
где R – внешний радиус трубки. Это уравнение основано на предположении, что после достижения критического веса, достаточного для преодоления сил поверхностного натяжения, вся выступившая капля отрывается целиком, оставляя кончик трубки "сухим". В действительности, как показано на рис. 5.3, при достижении критического веса капля вытягивается с образованием цилиндрической шейки, по которой происходит её разрыв. В результате только часть выступившей капли отрывается, а часть остаётся висеть на кончике трубки. Чтобы учесть остающуюся часть капли, необходимо вводить поправочный коэффициент Y
mg = 2p Rs×Y, (5.11а)
который зависит от радиуса R и кубического корня из объёма капли v:
Y = ¦ 
(5.12)
Эта функция является эмпирической и задаётся в виде таблицы или графика (рис. 5.4).
В сталагмометрическом методе вес капель определяют косвенно, путем подсчёта числа капель n, за которое истекает определённый объём испытуемой жидкости из капилляра. Для этой цели, капиллярная трубка имеет расширение, служащее резервуаром для жидкости (на рис. 5.3 оно не показано). Жидкость поднимают в трубку до верхней метки, расположенной выше расширения, и позволяют стекать пока мениск не опустится до нижней метки, расположенной ниже расширения. При этом подсчитывают число капель n. Если весь объём вытекшей жидкости составляет V, то средний объём v и средний вес mg капли могут быть вычислены по формулам
v = V/n (5.13)
mg = v×r×g (5.14)
где r - плотность жидкости. Комбинируя (5.14) и (5.11а) можно найти рабочее выражение для поверхностного натяжения
(5.15)
Объём V, необходимый для вычислений по уравнению (5.13), находится в отдельных калибровочных измерениях и является постоянным для данного сталагмометра. Однако радиус конца сталагмометра приходится определять периодически ·. Это может быть сделано с помощью экспериментов с жидкостью, поверхностное натяжение и плотность которой известны с хорошей точностью. Радиус R вычисляется по уравнению:
, (5.16)
в котором индекс ноль указывает на отношение данного параметра к калибровочной жидкости (в данной работе – к воде). Поскольку коэффициент Y в этом уравнении является функцией искомого радиуса R, вычисления приходится проводить путём последовательных приближений в соответствии с циклическим алгоритмом, описанным в табл. 5.1. Цикл обрывают, когда разница между двумя последовательными приближениями R становится равной или меньше некоторой приемлемой погрешности. Последнее приближение (например R ''') принимают в качестве искомого радиуса R и используют далее для вычислений поверхностного натяжения исследуемых растворов ПАВ.
Для применимости уравнения (5.11а) необходимо, чтобы капля жидкости, отрывающаяся от кончика капиллярной трубки, в момент отрыва находилась в равновесии с её паром в окружающей среде. Для этого важны две особенности экспериментальной установки. Во-первых, конец сталагмометра должен находиться в атмосфере насыщенных или близких к насыщению паров испытуемой жидкости. Это достигается тем, что его опускают по возможности низко над поверхностью соответствующей жидкости в приемнике. В наиболее точных измерениях приёмник жидкости изолируют от окружающей атмосферы крышкой с узким отверстием для сталагмометра, как показано на рис. 5.3, и термостатируют при определённой температуре до установления давления насыщенных паров над поверхностью жидкости. Однако этого не достаточно для обеспечения равновесия капля/пар, потому что поверхность жидкости в приёмнике является плоской, тогда как вытекающая из трубки капля имеет искривлённую поверхность. Как известно из уравнения Кельвина, давление паров Р над искривлённой поверхностью жидкости несколько отличается от давления паров над плоской поверхностью Р ¥: Р = 
где vm – молярный объём жидкости, r – радиус кривизны поверхности, равный радиусу шара в случае сферической капли. Поэтому давление паров, равновесное по отношению к капле, несколько отличается от того давления, которое является равновесным по отношению к плоской поверхности жидкости в приёмнике. Чтобы равновесие капля/пар устанавливалось более точно, скорость формирования капли на конце трубки должна быть по возможности низкой. Для этого внутренний диаметр капилляра должен быть очень малым. В наиболее точных измерениях скорость формирования каждой капли регулируют дополнительно, надев на верхний конец сталагмометра резиновую или другую эластичную трубку с устройством, регулирующим доступ воздуха (металлический зажим, стеклянный кран и т.д.). С помощью этого устройства позволяют капле сформироваться приблизительно на 80 % по объёму, затем перекрывают доступ воздуха и заставляют её висеть на конце сталагмометра несколько минут, после чего доступ воздуха открывают и дают капле сформироваться окончательно и вытечь.
Последовательность выполнения работы
1. Из исходного водного раствора олеата натрия С17Н33СООNa с концентрацией 1.00 г/л и дистиллированной воды готовят не менее шести разбавлений до наименьшей концентрации ~ 0.1 ммоль/л. Например, может быть использована следующая схема:
| объём исходного раствора олеата натрия, мл: | ||||||
| объём добавляемой воды, мл: | - | |||||
| концентрация приготовленного раствора, г/л: | 0.5 | 0.3 | 0.177 | 0.1 | 0.05 |
Предварительно необходимо убедиться, что температура растворов одинакова с точностью до 1 °С. Температуру растворов Т, а так же объём сталагмометра V, записывают в лабораторный журнал. (Если преподавателем или лаборантом не указано иначе, объём V следует принять 1.103 см3)
2. В сосуд (стаканчик или колбу), служащий приёмником жидкости, вытекающей из сталагмометра, наливают около 10 мл очередного раствора и опускают в него сталагмометр так, чтобы его нижний кончик был лишь немного выше уровня жидкости и много ниже краёв сосуда. Оставляют установку в таком виде на 5-10 минут для установления приблизительного равновесия жидкость/пар над поверхностью раствора.
3. Подняв приёмник так, чтобы кончик сталагмометра погрузился в исследуемый раствор, заполняют сталагмометр раствором выше верхней метки с помощью груши или вакуумного насоса. Отсоединяют грушу (или насос) и опускают приёмник. Когда мениск жидкости достигает верхней метки, начинают счёт числа капель и прекращают его, когда мениск жидкости достигает нижней метки. Число капель n записывают.
Скорость истечения жидкости должна составлять не более 1 капли в минуту. Если скорость оказывается больше, её регулируют, периодически закрывая и открывая вручную доступ воздуха в верхний конец капиллярной трубки.
4. Измерения начинают с дистиллированной воды и продолжают в порядке увеличения концентрации ПАВ, повторяя их по пп. 2 и 3 не менее трёх раз для каждого раствора.
Обработка и оформление результатов
1. Результаты измерения числа капель n для каждого раствора заносят в таблицу (см. табл. 5.2) и вычисляют средние числа капель 
.
2. Вычисляют средний объём v 0 капли воды (с = 0) по уравнению 5.13, используя среднее число капель 
. Вычисляют далее радиус R сталагмометра по алгоритму, данному в табл. 5.1. Значения s 0 и r 0 , необходимые для вычисления коэффициента В, следует найти интерполяцией данных в табл. П4.2 в приложении 4 для фактической температуры измерений. Промежуточные вычисления последовательных приближений Y и R удобно вести в отдельной таблице (табл. 5.3). Значения Y находят для данного 
по рис. 5.4. Вычисления продолжают до тех пор, пока последовательные приближения R iи R i-1не станут различаться на величину расхождения e =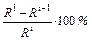 
, меньшую чем 0.5 %. После достижения этой точности, вычисления останавливают и последнее приближение R принимают за окончательное значение.
3. Вычисляют средний объём капли по уравнению 5.13 для каждого раствора ПАВ и соответствующие отношения 
. Эти значения следует занести в отдельную таблицу (см. табл. 5.4). Находят по рис. 5.4 коэффициенты Y для вычисленных значений 
. С помощью полученных значений v и Y вычисляют поверхностное натяжение s по уравнению 5.15. В отношении плотности r растворов ПАВ, входящей в уравнение 5.15, следует учесть, что при концентрациях менее 0.1 г/л она практически равна плотности воды при данной температуре (приложение 4, табл. П4.3)
4. Строят график зависимости s от концентрации. Следует пользоваться молярной концентрацией, поскольку именно в этой шкале принято сравнивать величины ККМ разных ПАВ. Обычно график имеет точку излома или изгиба при ККМ (рис. 5.5), которая бывает видна более отчетливо, когда в качестве переменной по оси абсцисс откладывается логарифм концентрации. Если, тем не менее, излом на полученной кривой не достаточно отчётлив, следует использовать графический способ, показанный на рис. 5.5: находят два приблизительно линейных участка на кривой и строят к ним касательные, абсцисса пересечения которых представляет искомое значение ККМ (логарифма ККМ, если использована логарифмическая шкала).
5. В качестве вывода из работы указать значение ККМ в молярной и весовой (г/л) шкалах концентрации.
Контрольные вопросы
1. Что называется дифильностью молекул? Как классифицируются дифильные ПАВ?
2. Какие особые свойства имеют растворы дифильных ПАВ в сравнении с растворами других веществ?
3. Что называется критической концентрацией мицеллообразования?
4. Что является движущей силой мицеллообразования?
5. Какие существуют теоретические объяснения ККМ?
6. Какую величину ККМ имеют большинство коллоидных ПАВ? Какие факторы на неё влияют?
7. Какие экспериментальные методы применяются для определения ККМ?
8. Как зависит электрическая проводность растворов дифильных ПАВ от концентрации? Отличается ли эта зависимость от того, что известно для обычных электролитов?
9. Как зависит поверхностное натяжение растворов дифильных ПАВ от концентрации? Чем отличается эта зависимость от той, что известна для обычных ПАВ, например для водных растворов бутилового спирта?
10. Что называется сталагмометром? Опишите принцип сталагмометрического определения поверхностного натяжения.
11. От чего зависит вес капли, отрывающейся от кончика сталагмометра?
12. От чего зависит точность определения s сталагмометрическим методом? Что является важным в этом методе для получения правильных результатов?
13. Почему поверхностное натяжение не изменяется при увеличении концентрации ПАВ выше ККМ?
14. Какую роль играет внутренний диаметр капилляра в методе сталагмометрического измерения s? Влияет ли он на вес капли, отрывающейся от кончика трубки сталагмометра?
15. Какой вид имеет уравнение Лэнгмюра для адсорбции ПАВ в областях концентраций меньше ККМ и больше ККМ?
Литература
Зимон А.Д., Балакирев А.А., Дехтяренко Н.Г., Бабак В.Г., Аксёнов В.Н. Коллоидная химия. Лабораторный практикум. Часть 1. М: ВЗИПП 1986, Лаб. работа 5.
Berthod A. Structures physico-chimiques des milieux disperses, micelles, emulsions et microemulsions. Journal de chimie physique 1983, vol. 80, p. 407-424 (о ККМ).
Адамсон А. Физическая химия поверхностей. (пер. с англ.) М: Мир 1979, Глава 1 (об определении s), Глава 11 (о ККМ).
Dickinson E., Stainsby G. Colloids in food. L: Applied Science 1982, Chapter 4 (о ККМ).
Мелвин-Хьюз Э.А. Физическая химия. Том 2. (пер. с англ.) М: Издатинлит 1962, Глава 19 (об определении s).
Micelles, membranes, microemulsions, and monolayers. (Ed. W.M. Gelbart, A. Ben-Shaul, D. Roux) N.Y.: Springer-Verlag, 1994, Chapter 1 (рисунок 5.2)
Harkins W.D., Brown F.E. The determination of surface tension (free surface energy), and the weight of falling drop. Journal of the American Chemical Society 1919, vol. 41, 499-524 (эксперимнтальные точки для рис. 5.4)
Бовкун О.П., Маркина З.Н., Гракова Т.С. Определение критической концентрации мицеллообразования водных растворов мыл с добавками диоксана, метилового спирта и этиленгликоля. Коллоидный журнал 1970, том 32, 327-332 (эксперимнтальные точки для рис. 5.5)
Рис. 5.1 (а, б) Распределение растворенного вещества между ассоциированными молекулами (x, в долях единицы) и неассоциированными молекулами (1–x) при некоторых произвольных значениях констант равновесий. (мМ – ммоль/л) (в) – зависимость абсолютных концентраций ассоциированных и неассоциированных молекул ПАВ от общей концентрации С при n = 100.
Рис. 5.2 Зависимость некоторых свойств J от концентрации типичного ПАВ (додецилсульфата натрия) вблизи ККМ
Рис. 5.3 Схематическое изображение капли, вытекающей из кончика капиллярной трубки. Кончик находится в стеклянном приёмнике над поверхностью жидкости, которую наливают за некоторое время до начала капания из трубки.
Рис. 5.4 Поправочный коэффициент Y как функция отношения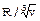 
. При 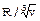> 0.3 следует пользоваться рис (а), при 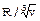< 0.3 – рис. (б)
Рис. 5.5 (образец) Изменение поверхностного натяжения в интервале концентраций, охватывающем ККМ. Показаны элементы графических построений, которые могут быть полезны для более надёжного определения этой точки.
· внешняя окружность конца сталагмометра должна быть очень гладкой. Поэтому её подвергают периодической шлифовке.
