До сих пор мы говорили о состоянии системы (на микро- или макроуровнях) в какой-то определённый момент времени. Перейдём к рассмотрению процессов.
Термодинамические параметры, можно разделить на внешние и внутренние. Внешние параметры характеризуют внешние условия, в которых находится система. Изменение этих параметров будем считать настолько медленными, что в каждый момент времени состояние системы можно рассматривать как равновесное. Такие процессы называются квазистатическими. Они обратимы. Если внешние параметры или температура термостата проходят через те же значения в обратном порядке, то и система проходит через те же равновесные состояния в обратном порядке.
Из выражения (2.2.1) следует, что изменение внутренней энергии макроскопической системы можно представить в виде:
(2.2.4)
Здесь 
– изменение энергетических уровней системы при очень малом изменении её внешних параметров 
:
.
При этом распределение вероятностей микросостояний остаётся неизменным. Величина 
– сила, действующая на систему при изменении i -ого энергетического уровня вследствие изменения параметра 
. Подставляя 
в первое слагаемое правой части соотношения (2.2.4), получаем:
.
Здесь 
– средняя обобщенная сила, действующая на подсистему при изменении параметра . Таким образом,
(2.2.5)
есть работа, производимая над подсистемой при изменении внешних параметров на величину 
. Например, если – высота поршня h в цилиндре с газом, то 
, где р – давление газа, S – площадь поршня. Тогда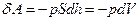 
, где dV – изменение объёма подсистемы (газа в цилиндре). 
не является полным дифференциалом какого-либо выражения. Обобщённая сила 
зависит от внешних параметров и температуры 
. Работа, произведённая над системой при изменении параметра :
зависит от пути интегрирования. Нельзя определить работу, зная только начальное и конечное состояние системы, она не является функцией состояния.
Второе слагаемое в соотношении (2.2.4) преобразуем следующим образом:
(2.2.6)
Поскольку 
, то получаем 
. Так как 
, то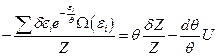 
.
Подставляем последнее выражение в (2.2.6):
.
Для макроскопической системы: 
.
Следовательно 
и 
. Поскольку энтропия 
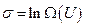есть функция состояния, то элементарное изменение этой величины 
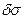заменяем дифференциалом 
.
Если энергетические уровни системы остаются неизменными (внешние параметры не меняются), то энергия, подводимая к системе или отдаваемая ею, идёт на изменение распределения вероятностей микросостояний. Изменение энергии подсистемы возникает вследствии непосредственного взаимодействия частиц среды и подсистемы. Эту часть изменения энергии называют количеством теплоты 
. Таким образом:
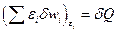(2.2.7)
Для квазистатических процессов:
(2.2.8)
Подставляя (2.2.5) и (2.2.7) в соотношение (2.2.4) находим полное изменение внутренней энергии системы:
(2.2.8)
Для квазистатических процессов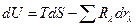 
. Если внешний параметр – объём системы V, то
(2.2.9)
Это одно из важнейших термодинамических соотношений.
Количество теплоты , так же как и работа, не является функцией состояния. Количество теплоты , которым подсистема обменивается с окружающей средой, зависит от процесса. Функция состояния – это функция, которая в заданном состоянии системы имеет вполне определённое значение независимо от того, каким путём или способом система в это состояние приводится. Для функции состояния интеграл по замкнутому циклу изменения состояний равен нулю. Например 
, для обратимых процессов 
.
2.4. Второе начало термодинамики и «стрела времени».
