Упорядоченная тройка некомпланарных векторов 
, 
, 
с общим началом в точке O называется правой, если кратчайший поворот от вектора к вектору , наблюдаемый из конца вектора , происходит против движения часовой стрелки. В противном случае тройка называется левой.
Векторным произведением векторов и называется вектор , обозначаемый = 
, который удовлетворяет следующим трем условиям:
1) 
;
2) ^ , ^ ;
3) тройка , , – правая.
Основные свойства векторного произведения векторов:
1) = – ( );
2) (λ ) = λ ( ) = (λ );
3) ( + ) = + ;
4) = 0 
|| ;
5) | | = S, где S – площадь параллелограмма, построенного на векторах и , имеющих общее начало в точке O.
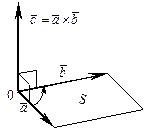
Если = (x 1, y 1, z 1), = (x 2, y 2, z 2), то векторное произведение выражается через координаты данных векторов и следующим образом:
.
С помощью векторного произведения можно вычислить вращающий момент M силы 
, приложенной к точке B тела, закрепленного в точке A: M = 
.
Пример. Вычислить координаты вращающего момента M силы = (3, 2, 1), приложенной к точке A (– 1, 2, 4), относительно начала координат O.
►Имеем
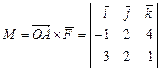= (– 6, 13, – 8).◄
Смешанное произведение векторов и его приложения
Смешанным произведением векторов , , называется число ( )· .
Основные свойства смешанного произведения векторов:
1) ( )· = ·( ), поэтому смешанное произведение можно обозначить проще: ;
2) = = = – = – = – ;
3) = 0 , , компланарны.
Если = (x 1, y 1, z 1), = (x 2, y 2, z 2), = (x 3, y 3, z 3), то
= 
.
4) геометрический смысл смешанного произведения заключается в следующем: = ± V, где V – объем параллелепипеда, построенного на перемножаемых векторах, взятый со знаком «+», если тройка векторов , , – правая, или со знаком «–», если она левая;
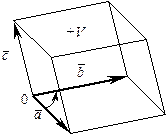
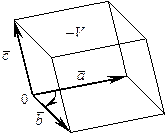
Объем V пар параллелепипеда, построенного на векторах , и , и объем V пир образованной ими треугольной пирамиды находятся по формулам
V пар = 
, V пир = 
.
Задание 2
2.1. Даны векторы , и . Необходимо:
а) вычислить смешанное произведение трех векторов;
б) найти модуль векторного произведения;
в) вычислить скалярное произведение двух векторов;
г) проверить, будут ли коллинеарны или ортогональны два вектора;
д) проверить, будут ли компланарны три вектора.
2.1.1. = 2 
– 3 
+ 
, = + 4 , = 5 + 2 – 3 ;
а) , 3 , ; б) 3 , 2 ; в) , – 4 ; г) , ; д) , 2 , .
2.1.2. = 3 + 4 + , = – 2 + 7 , = 3 – 6 + 21 ;
а) 5 , 2 , ; б) 4 , 2 ; в) , ; г) , ; д) 2 , – 3 , .
2.1.3. = 2 – 4 – 2 , = 7 + 3 , = 3 + 5 – 7 ;
а) , 2 , 3 ; б) 3 , – 7 ; в), , – 2 ; г) , ; д) 3 , 2 , 3 .
2.1.4. = – 7 + 2 , = 2 – 6 + 4 , = – 3 + 2 ;
а) , – 2 , – 7 ; б) 4 , 3 ; в) 2 , – 7 ; г) , ; д) 2 , 4 , 3 .
2.1.5. = – 4 + 2 – , = 3 + 5 – 2 , = + 5 ;
а) , 6 , 3 ; б) 2 , ; в) , – 4 ; г) , ; д) , 6 , 3 .
2.1.6. = 3 – 2 + , = 2 – , = – 3 + 2 – ;
а) , – 3 , 2 ; б) 5 , 3 ; в) – 2 , 4 ; г) , ; д) 5 , 4 , 3 .
2.1.7. = 4 – + 3 , = 2 + 3 – 5 , = 7 + 2 + 4 ;
а) 7 , – 4 , 2 ; б) 3 , 5 ; в) 2 , 4 ; г) , ; д) 7 , 2 , 5 .
2.1.8. = 4 + 2 – 3 , = 2 + , = – 12 – 6 + 9 ;
а) 2 , 3 , ; б) 4 , 3 ; в) , – 4 ; г) , ; д) 2 , 3 , – 4 .
2.1.9. = – + 5 , = – 3 + 2 + 2 , = – 2 – 4 + ;
а) 3 , – 4 , 2 ; б) 7 , – 3 ; в) 2 , 3 ; г) , ; д) 7 , 2 , – 3 .
2.1.10. = 6 – 4 + 6 , = 9 – 6 + 9 , = – 8 ;
а) 2 , – 4 , 3 ; б) 3 , – 9 ; в) 3 , – 5 ; г) , ; д) 3 , – 4 , – 9 .
2.1.11. = 5 – 3 + 4 , = 2 – 4 – 2 , = 3 + 5 – 7 ;
а) , –4 , 2 ; б) – 2 , 4 ; в) – 3 , 6 ; г) , ; д) , –– 2 , 6 .
2.1.12. = – 4 + 3 – 7 , = 4 + 6 – 2 , = 6 + 9 – 3 ;
а) – 2 , , – 2 ; б) 4 , 7 ; в) 5 , – 3 ; г) , ; д) – 2 , 4 , 7 .
2.1.13. = – 5 + 2 – 2 , = 7 – 5 , = 2 + 3 – 2 ;
а) 2 , 4 , – 5 ; б) – 3 , 11 ; в) 8 , – 6 ; г) , ; д) 8 , – 3 , 11 .
2.1.14. = – 4 – 6 + 2 , = 2 + 3 – , = – + 5 – 3 ;
а) 5 , 7 , 2 ; б) – 4 , 11 ; в) 3 , – 7 ; г) , ; д) 3 , 7 , – 2 .
2.1.15. = – 4 + 2 – 3 , = – 3 + 5 , = 6 + 6 – 4 ;
а) 5 , – , 3 ; б) – 7 , 4 ; в) 3 , 9 ; г) , ; д) 3 , – 9 , 4 .
2.1.16. = – 3 + 8 , = 2 + 3 – 2 , = 8 + 12 – 8 ;
а) 4 , – 6 , 5 ; б) – 7 , 9 ; в) 3 , – 8 ; г) , ; д) 4 , – 6 , 9 .
2.1.17. = 2 – 4 – 2 , = – 9 + 2 , = 3 + 5 – 7 ;
а) 7 , 5 , – ; б) – 5 , 4 ; в) 3 , – 8 ; г) , ; д) 7 , 5 , – .
2.1.18. = 9 – 3 + , = 3 – 15 + 21 , = – 5 + 7 ;
а) 2 , – 7 , 3 ; б) – 6 , 4 ; в) 5 , 7 ; г) , ; д) 2 , – 7 , 4 .
2.1.19. = – 2 + 4 – 3 , = 5 + – 2 , = 7 + 4 – ;
а) , – 6 , 2 ; б) – 8 , 5 ; в) – 9 , 7 ; г) , ; д) , – 6 , 5 .
2.1.20. = – 9 + 4 – 5 , = – 2 + 4 , = – 5 + 10 – 20 ;
а) – 2 , 7 , 5 ; б) – 6 , 7 ; в) 9 , 4 ; г) , ; д) – 2 , 7 , 4 .
2.1.21. = 2 – 7 + 5 , = – + 2 – 6 , = 3 + 2 – 4 ;
а) – 3 , 6 , – ; б) 5 , 3 ; в) 7 , – 4 ; г) , ; д) 7 , – 4 , 3 .
2.1.22. = 7 – 4 – 5 , = – 11 + 3 , = 5 + 5 + 3 ;
а) 3 , – 7 , 2 ; б) 2 , 6 ; в) – 4 , – 5 ; г) , ; д) – 4 , 2 , 6 .
2.1.23. = 4 – 6 – 2 , = – 2 + 3 + ,
|
|
|
|
|
|
Дата добавления: 2015-11-05; Мы поможем в написании ваших работ!; просмотров: 1897 | Нарушение авторских прав
Лучшие изречения: