В последние десятилетия использование портфельной теории значительно расширилось. Все большее число инвестиционных менеджеров, управляющих инвестиционных фондов применяют ее методы на практике, и хотя у нее имеется немало противников, ее влияние постоянно растет не только в академических кругах, но и на практике, включая российскую. Присуждение Нобелевских премий по экономике ее создателям и разработчикам является свидетельством этого.
Под инвестированием в широком смысле понимается любой процесс, имеющий целью сохранение и увеличение стоимости денежных или других средств. Средства, предназначенные для инвестирования, представляют собой инвестиционный капитал. С течением времени этот капитал может принимать различные конкретные формы.
Из определения инвестирования видна важнейшая роль двух факторов: времени и стоимости. Важнейший принцип инвестирования состоит в том, что стоимость актива меняется со временем.
Со временем связана еще одна характеристика процесса инвестирования – риск. Хотя инвестиционный капитал имеет вполне определенную стоимость в начальный момент времени, его будущая стоимость не известна. Для инвестора эта будущая стоимость есть ожидаемая величина.
Одним из традиционных методов оценки и управления риском считается статистический метод. Основными инструментами статистического анализа являются – дисперсия, стандартное отклонение, коэффициент вариации. Суть этого метода состоит в анализе статистических данных за возможно больший период времени.
Под инвестиционным портфелем понимается некая совокупность ценных бумаг, принадлежащих физическому или юридическому лицу, либо юридическим или физическим лицам, выступающая как целостный объект управления. Обычно на рынке продается некое инвестиционное качество с заданным соотношением Риск / Доход, которое в процессе управления портфелем может быть улучшено.
Основная задача портфельного инвестирования – улучшить условия инвестирования, придав совокупности ценных бумаг такие инвестиционные характеристики, которые недостижимы с позиции отдельно взятой ценной бумаги, и возможны только при их комбинации.
Выбор ценных бумаг для портфельного инвестирования зависит от целей инвестора и его отношения к риску. Для всех инвесторов принято выделять три типа целей инвестирования и связанного с ними отношения к риску.
Инвестор стремится защитить свои средства от инфляции; для достижения цели он предпочитает вложения с невысокой доходностью, но с низким риском. Этот тип инвестора называют консервативным.
Инвестор пытается произвести длительное вложение капитала, обеспечивающее его рост. Для достижения этой цели он готов пойти на рискованные вложения, но в ограниченном объеме, подстраховывая себя вложениями в слабодоходные, но и малорискованные ценные бумаги. Такой тип инвестора называют умеренно-агрессивным.
Инвестор стремится к быстрому росту вложенных средств, готов для этого делать вложения в рискованные ценные бумаги, быстро менять структуру своего портфеля, проводя спекулятивную игру на курсах ценных бумаг. Этот тип инвестора принято называть агрессивным.
На практике используют множество методик формирования оптимальной структуры портфеля ценных бумаг. Большинство из них основано на методике Марковица. Он впервые предложил математическую формализацию задачи нахождения оптимальной структуры портфеля ценных бумаг в 1951 году, за что позднее был удостоен Нобелевской по экономике.
Основная идея модели Марковица заключается в том, чтобы статистически рассматривать будущий доход, приносимый финансовым инструментом, как случайную переменную, то есть доходы по отдельным инвестиционным объектам случайно изменяются в некоторых пределах. Тогда, если неким образом случайно определить по каждому инвестиционному объекту вполне определенные вероятности наступления, можно получить распределение вероятностей получения дохода по каждой альтернативе вложения средств. Это получило название вероятностной модели рынка. Для упрощения модель Марковица полагает, что доходы распределены нормально.
По модели Марковица определяются показатели, характеризующие объем инвестиций и риск, что позволяет сравнивать между собой различные альтернативы вложения капитала с точки зрения поставленных целей и тем самым создать масштаб для оценки различных комбинаций.
В качестве масштаба ожидаемого дохода из ряда возможных доходов на практике используют наиболее вероятное значение, которое в случае нормального распределения совпадает с математическим ожиданием.
Для измерения риска служат показатели рассеивания, поэтому, чем больше разброс величин возможных доходов, тем больше опасность, что ожидаемый доход не будет получен.
Таким образом, любой портфель ценных бумаг характеризуется двумя величинами:
1) Ожидаемой доходностью
, (11)
где 
– доля общего вложения, приходящаяся на 
-ю ценную бумагу;
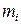– ожидаемая доходность -ой ценной бумаги, в %;
– ожидаемая доходность портфеля, в %.
2) Мерой риска – среднеквадратическим отклонением доходности от ожидаемого значения
(12)
где 
– мера риска портфеля;
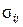– ковариация между доходностями -ой и 
-ой ценных бумаг;
и 
– доли общего вложения, приходящиеся на -ю и -ю ценные бумаги;
– число ценных бумаг портфеля.
Проблема заключается в численном определении относительных долей ценных бумаг в портфеле, которые наиболее выгодны для владельца. Марковиц ограничивает решение модели тем, что из всего множества «допустимых» портфелей, т.е. удовлетворяющих ограничениям, необходимо удалить те, которые рискованнее, чем другие.
Отобранные таким образом портфели объединяют в список, содержащий сведения о процентном составе портфеля из отдельных ценных бумаг, а также о доходе и риске портфелей.
Объяснение того факта, что инвестор должен рассмотреть только подмножество возможных портфелей, содержится в следующей теореме об эффективном множестве: «Инвестор выберет свой оптимальный портфель из множества портфелей, каждый из которых обеспечивает максимальную ожидаемую доходность для некоторого уровня риска».
На рис. 23 представлены недопустимые, допустимые и эффективные портфели, а также линия эффективного множества.
Рис. 23. Допустимое и эффективное множества
Задание
На рынке обращается 6 ценных бумаг ЦБ-1 – ЦБ-6. Известна доходность (в %) этих ценных бумаг за последние 5 периодов (табл. 1):
Таблица 1
Доходность ценных бумаг за последние 5 периодов, в %
| Период | ЦБ-1 | ЦБ-2 | ЦБ-3 | ЦБ-4 | ЦБ-5 | ЦБ-6 |
| 17,08 | 16,40 | 17,25 | 16,39 | 16,14 | 16,55 | |
| 16,74 | 16,00 | 17,10 | 16,14 | 15,99 | 16,18 | |
| 16,59 | 15,65 | 17,01 | 15,99 | 16,24 | 16,59 | |
| 17,01 | 15,85 | 16,61 | 16,48 | 15,93 | 16,39 | |
| 16,43 | 15,74 | 16,57 | 16,02 | 15,73 | 16,31 |
Необходимо:
1. Определить ковариации между доходностями каждой пары ценных бумаг.
2. Определить доходность и риск портфеля.
3. Найти с помощью надстройки «Поиск решения» в Microsoft Excel минимальный риск портфеля.
4. Найти с помощью надстройки «Поиск решения» в Microsoft Excel риск, получаемый при максимальной доходности портфеля.
5. Построить эффективное множество портфелей ценных бумаг по модели Марковица и выбрать на нем портфель с приемлемым соотношением доходности и риска.
6. Построить в Microsoft Excel график зависимости риска портфеля от максимального значения дохода, достигаемого при этом риске.
7. Выбрать портфели для инвесторов консервативного, умеренно-агрессивного и агрессивного типов, обосновав свой выбор.
Решение.
1. Определим ковариации между доходностями каждой пары ценных бумаг.
Для этого создаем в Microsoft Excel новую книгу и сохраняем ее под названием «Портфель ценных бумаг». На листе 1 новой книги в ячейки А1:G7 вводим исходные данные задачи, как на рис. 24.
Рис. 23. Ввод исходных данных задачи 3
Далее в ячейках А11:G17 формируем таблицу для расчета ковариационной матрицы, в ячейки В12:В17 вводим формулы с использованием встроенной функции «КОВАР» (категория «Статистические»), в качестве параметров которой указываются диапазоны ячеек с доходностями соответствующих ценных бумаг за все периоды (рис. 25).
Рис. 24. Ввод формул для определения ковариации
Затем скопируем формулы в ячейках В12:В17 в остальные ячейки данной таблицы, в результате получим следующее:
Рис. 25. Ковариационная матрица (результат вычисления)
Итак, получили ковариационную матрицу, элементами которой являются ковариации между доходностями каждой пары ценных бумаг.
2. Определим доходность и риск портфеля
Сначала найдем математическое ожидание доходности каждой ценной бумаги. Математическое ожидание доходности вычисляется как среднее значение доходности, полученной во всех периодах. Определим математические ожидания каждой ценной бумаги в ячейках В8:G8 с помощью встроенной функции «СРЗНАЧ» Microsoft Excel (рис. 26).
Рис. 26. Определение математических ожиданий
Для определения доходности и риска портфеля добавим к ковариационной матрице напротив обозначения каждой ценной бумаги столбец с долей этой ценной бумаги в портфеле (в ячейки Н12:Н17) вводим нулевые первоначальные значения), ниже которого вводим формулу суммы долей (рис. 27). Для удобства нахождения риска портфеля продублируем с помощью равенства столбец долей ценных бумаг в строку (ячейки В18:G18).
Рис. 27. Ввод формулы для определения суммы долей ценных бумаг в портфеле
Для нахождения риска портфеля по формуле (12) сначала составим таблицу со значениями (
) для всех и : в ячейку В22 вводим формулу: «=$H12*B$18*B12», затем копируем ее во все остальные ячейки таблицы нахождения риска портфеля (рис. 28).
Все значения полученной таблицы будут равны нулю, поскольку доля ценных бумаг в портфеле не задана.
Рис. 28. Нахождение риска портфеля (промежуточные расчеты)
Для окончательного расчета риска портфеля по формуле (12) в отдельную ячейку В29 вводим формулу суммы всех значений таблицы нахождения риска портфеля: «=СУММ(B22:G27)».
Ниже, в ячейку В30, вводим формулу (11) расчета ожидаемой доходности портфеля: «=СУММПРОИЗВ(B8:G8;B18:G18)».
В результате в ячейках В29 и В30 получим значения риска и доходности портфеля соответственно (рис. 29).
Рис. 29. Вычисление риска и доходности портфеля
Значения риска и доходности портфеля в ячейках В29 и В30 будут равны нулю до тех пор, пока не будут заданы доли ценных бумаг в портфеле, после чего пересчет произойдет автоматически (рис. 29).
3. Найдем с помощью надстройки «Поиск решения» в Microsoft Excel минимальный риск портфеля ценных бумаг, т.е. найдем такую структуру портфеля (доли ценных бумаг), чтобы риск портфеля принимал минимальное значение при соблюдении определенных условий.
Для этого необходимо выделить ячейку, содержащую значение риска портфеля (ячейку В29), и выполнить команду «Сервис»/ «Поиск решения…»[1]. В открывшемся окне надстройки «Поиск решения…» в поле «Целевая ячейка» уже будет указано: «$B$29» (т.е. ячейка, содержащая значение риска портфеля), необходимо установить флажок «Равной минимальному значению», в поле «Изменяя ячейки» – выбрать «$H$12:$H$17», т.е. ячейки со значениями доли каждой ценной бумаги в портфеле (рис. 30). Далее указываем ограничения следующим образом: нажимаем кнопку «Добавить», и в открывшемся окне вводим ограничение неотрицательности доли ценных бумаг в портфеле (рис. 31), еще раз нажимаем кнопку «Добавить» и вводим ограничение на сумму долей ценных бумаг, которое должно быть равно 1 (рис. 32), нажимаем «ОК». В окне поиска решений (рис. 30) нажимаем «Выполнить».
Рис. 30. Окно "Поиск решений"
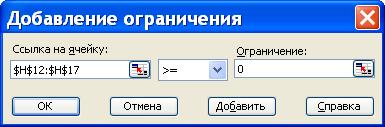
Рис. 31. Ввод первого ограничения
Рис. 32. Ввод второго ограничения
В результате получим минимальный риск портфеля, равный 0,022 – ячейка В29, а также долю каждой ценной бумаги в портфеле – ячейки Н12:Н17 (рис. 33).
Рис. 33. Минимальный риск портфеля
4. Аналогично с помощью надстройки «Поиск решения» в Microsoft Excel найдем риск, получаемый при максимальной доходности портфеля, т.е. найдем такую структуру портфеля (доли ценных бумаг), чтобы доходность портфеля принимала максимальное значение при соблюдении определенных условий.
Для этого необходимо выделить ячейку, содержащую значение доходности портфеля (ячейку В30), и выполнить команду «Сервис»/ «Поиск решения…». В открывшемся окне надстройки «Поиск решения…» в поле «Целевая ячейка» уже будет указано: «$B$30», необходимо установить флажок «Равной максимальному значению», в поле «Изменяя ячейки» – выбрать «$H$12:$H$17», далее указываем все ограничения (рис. 34).
Рис. 34. Окно «Поиск решения»
В результате риск портфеля, соответствующий его максимальной доходности в 15,808% (ячейка В30), составит 0,100 (ячейка В29), доли ценных бумаг в портфеле представлены в ячейках Н12:Н17 (рис. 35).
Рис. 35. Максимальная доходность портфеля
5. Построим эффективное множество портфелей ценных бумаг по модели Марковица и выберем на нем портфель с приемлемым соотношением доходности и риска.
Эффективное множество портфелей можно построить с помощью надстройки «Поиск решения» в Microsoft Excel, т.е. при заданном значении риска портфеля (стандартного отклонения портфеля), рассчитанного по формуле (12), необходимо максимизировать величину дохода, полученного при помощи формулы (11).
Диапазон, в котором лежат значения риска портфелей, составляющих эффективное множество, имеет нижнюю границу, равную минимальному риску портфеля ценных бумаг, и верхнюю границу, равную риску при максимальной доходности портфеля.
Теперь определим максимальную доходность портфеля и его структуру (т.е. доли в нем ценных бумаг), зафиксировав значение риска в этом диапазоне с некоторым шагом, например 0,01 (последним значением риска возьмем не 0,102, т.к. это значение выходит за допустимый диапазон риска, а верхнюю границу диапазона – 0,100).
Для поиска решения при риске 0,022 добавим новое ограничение «$B$29=0,022». Тогда окно поиска решений будет выглядеть следующим образом (рис. 36)[2]:
Рис. 36. Расчет максимальной доходности при риске 0,022
В результате для риска 0,022 получим следующие результаты: доходность составляет 15,457%, доля ЦБ-1=0, доля ЦБ-2=0, доля ЦБ-3=0,41, доля ЦБ-4=0,46, доля ЦБ-5=0, доля ЦБ-6=0,13.
Поскольку при новом поиске решения полученные результаты изменятся на новые, то создадим таблицу, в которую будем вводить все результаты вычислений при различных значениях риска. Запишем полученные при риске 0,022 результаты в отдельные ячейки B33:I33 (рис. 37).
Рис. 37. Результат вычисления при риске 0,022
Теперь определим максимальную доходность портфеля и его структуру, зафиксировав значение риска на следующем шаге (0,022+0,01). Для этого изменим первое ограничение на «$B$29=0,032». Получим следующие результаты, которые перенесем в ячейки B34:I34, и т.д.
Определив показатели для всех значений риска в диапазоне от минимального до максимального с некоторым шагом (в данном примере 0,01) и сохранив результаты в отдельных ячейках (в т.ч. и значения долей ценных бумаг в портфеле, при которых получается данное значение риска), получим эффективное множество портфелей ценных бумаг, в которое входят портфели, обеспечивающие максимальную ожидаемую доходность для диапазона уровня риска от 0,022 до 0,100. Эффективное множество портфелей ценных бумаг представлено в ячейках А32:I41 (рис. 38).
Выбрать на нем портфель с приемлемым соотношением доходности и риска
6. Построим в Microsoft Excel график зависимости риска портфеля от максимального значения дохода, достигаемого при этом риске.
Для этого выделяем значения столбцов «Риск» и «Доход» эффективного множества портфелей ценных бумаг, затем выполняем команду «Вставка»/ «Диаграмма», в открывшемся окне выбираем тип «Точечная». Пройдя все шаги построения диаграммы и указав все ее параметры, получает следующий график зависимости риска портфеля от максимального значения дохода, достигаемого при этом риске (рис. 38):
Рис. 38. Зависимость дохода от риска
7. Выберем портфели для инвесторов консервативного, умеренно-агрессивного и агрессивного типов.
Конечный выбор портфеля инвестором зависит от его стратегии поведения на рынке. Консервативный инвестор выберет 1-й портфель (вложит 41% средств в ЦБ-3, 46% в ЦБ-4 и 13% в ЦБ-6), при этом инвестор получит минимальную доходность при минимуме риска.
Если инвестор намерен вести политику агрессивного роста стоимости портфеля, то он выберет 3-й или 4-й портфель, т.к. они обеспечивают высокую доходность, правда при достаточно большом риске нестабильности получения дохода. Выбор инвестором 5-9-го портфелей маловероятен, т.к. они дают практически такую же доходность, как и 3-й или 4-й портфель, но при заметном увеличении риска.
Умеренно-агрессивный инвестор, скорее всего, выберет 2-й портфель, поскольку он готов пойти на рискованные вложения, но в ограниченном объеме, подстраховывая себя вложениями в слабодоходные, но и малорискованные ценные бумаги.
