При подборе теоретического закона распределения необходимо знать, что опытная исходная информация об изменениях случайной величины обычно представляет собой некоторую выборку из всей генеральной совокупности возможных значений случайной величины. Поэтому статистический ряд распределения и кривая накопленных опытных вероятностей содержат ошибки исходной информации.
Однако этих ошибок можно избежать, если при определении показателей надежности изделий (в частности, доремонтного ресурса гильз цилиндров) правильно подобрать и использовать теоретический закон распределения (ТЗР), характеризующий соотношение между возможными значениями случайной величины и их вероятностью.
Замена опытного закона распределения теоретическим называется сглаживанием или выравниванием статистической информации. Теоретический закон применяют как к полной совокупности, так и к любой частной совокупности данного наименования.
ТЗР известен, если определены теоретическая дифференциальная f(T) и теоретическая интегральная F(T) функции распределения. Применительно к надежности с.-х. техники используются, главным образом, закон нормального распределения (ЗНР) и закон распределения Вейбулла (ЗРВ).
Предварительный выбор ТЗР осуществляется по величине коэффициента вариации (V). Если V<0,3 то распределение подчиняется ЗНР, если V>0,5 – ЗРВ. Если V лежит в интервале от 0,3 до 0,5, то выбирается тот закон, который лучше совпадает с опытной информацией. Точность совпадения оценивается по критерию согласия.
В нашем случае коэффициент вариации V=0,5, поэтому подходит как ЗНР, так и ЗРВ. Для окончательного решения о выборе ТЗР необходимо рассчитать дифференциальную f(T) и интегральную F(T) функции распределения ресурса детали по ЗНР и ЗРВ, а затем с помощью критерия согласия выбрать ТЗР.
Дифференциальная функция ЗНР определяется по формуле:
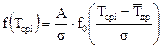, (11)
где А – протяженность интервала, мото-ч.;
s – среднее квадратическое отклонение, мото-ч.;
Тсрi – середина i-го интервала, мото-ч.;
f0 – центрированная дифференциальная функция (табулирована, ее значение определяется по таблице Б2 приложения Б).
Необходимо учитывать, что:
f0(-T)=f0(T) (12)
Расчет ведется для каждого интервала.
В нашем примере для первого интервала:
Значение f0(-1,47) находится по таблице Б2 приложения Б, для чего в первой вертикальной колонке 
находим строку 1,4, а в седьмой вертикальной колонке 7, получаем f0=0,14.
Для второго интервала:
Аналогичные расчеты проводят и для остальных интервалов:
Полученные данные заносят в таблицу 3.
Значение интегральной функции F(Tki) ЗНР в конце i-го интервала определяется по формуле:
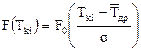, (13)
где F0 – центрированная интегральная функция (табулирована, ее значение определяется по таблице Б3 приложения Б);
Ткi – значение ресурса в конце i-го интервала статистического ряда;
– среднее значение ресурса;
s – среднее квадратическое отклонение.
Необходимо помнить, что:
F0(-T)=1-F0(+T). (14)
Расчет ведется для каждого интервала.
Для нашего примера конец первого интервала Ткi=1478 мото-ч.
Полученные значения интегральных функций записывают в таблицу 3.
Дифференциальная функция ЗРВ определяется по формуле:
, (15)
где А – протяженность интервала в мото-ч;
а – параметр ЗРВ, мото-ч;
tсм – смещение начала рассеивания, мото-ч;
fТ – центрированная дифференциальная функция (табулирована и ее значение определяют по таблице Б5 приложения Б).
. (16)
Коэффициенты ЗРВ (Кв, b, Sв) в зависимости от коэффициента вариации V определяют по таблице Б4 приложения Б.
В нашем случае V=0,5.
Следовательно: b=2,1; Кв=0,886; Sв=0,567.
.
Расчет f(Tсрi) для ЗРВ ведется для каждого интервала и полученные данные также заносят в таблицу 3.
Значения дифференциальной функции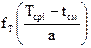 
определяют при необходимости с использованием двойного интерполирования по b и 
.
Ниже приводится пример использования двойного интерполирования для определения значения fT.
Воспользуемся выпиской из таблицы Б5 приложения Б.
| Параметр b | ||
| 2,0 | 2,1 | 3,0 | |
| 0,20 0,22 0,30 | 0,38 Х1 0,55 | Х | 0,12 Х2 0,26 |
Сначала находят значения Х1 и Х2 интерполированием с использованием следующего соотношения:
;
откуда
Затем определяют искомое значение 
=Х, применяя следующие соотношения:
.
Тогда Х=0,41– 
, следовательно, fT(0,22)=0,38 при b=2,1.
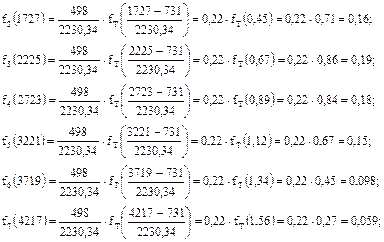
Интегральная функция ЗРВ определяется по формуле:
, (17)
где F(Tki) – интегральная функция ЗРВ в конце i-го интервала;
FT – табулированное значение интегральной функции (см. таблицу Б6 приложения Б);
tсм – смещение начала рассеивания;
а – параметр ЗРВ.
Для нашего примера:
Полученные расчетным путем значения для функций ЗНР и ЗРВ заносят в таблицу 3.
Окончательный выбор теоретического закона распределения ресурсов выполняют с помощью критерия согласия. Применительно к показателям надежности с.-х. техники чаще всего используют критерий Пирсона (χ2) и критерий Колмогорова (
). По величине критерия согласия можно определить вероятность совпадения опытных и теоретических законов и на этом основании принять или отбросить выбранный теоретический закон распределения, или обоснованно выбрать один теоретический закон из двух или нескольких.
Таблица 3 – Выбор теоретического закона распределения ресурсов
| Интервал, мото-ч. | 980-1478 | 1478-1976 | 1976-2474 | 2474-2972 | 2972-3470 | 3470-3968 | 3968-4466 | 4466-4964 | 4964-5462 | |
| Конец интервала, мото-ч | ||||||||||
| Середина интервала, мото-ч | ||||||||||
| ЗНР | f(T) | 0,07 | 0,12 | 0,17 | 0,20 | 0,17 | 0,12 | 0,06 | 0,03 | 0,01 |
| F(T) | 0,11 | 0,23 | 0,41 | 0,60 | 0,77 | 0,89 | 0,96 | 0,99 | 1,00 | |
| ЗРВ | f(T) | 0,084 | 0,16 | 0,19 | 0,18 | 0,15 | 0,098 | 0,059 | 0,027 | 0,013 |
| F(T) | 0,098 | 0,26 | 0,44 | 0,63 | 0,79 | 0,89 | 0,94 | 0,98 | 0,99 |
Следует помнить, что критической вероятностью совпадения принято считать Р=10%. Если Р<10%, то выбранный для выравнивания опытной информации теоретический закон распределения следует считать недействительным.
Критерий согласия Пирсона определяют по формуле:
, (18)
где ny – число интервалов в укрупненном статистическом ряду;
mTi – теоретическая частота в i-ом интервале статистического ряда;
mi – опытная частота в i-ом интервале статистического ряда.
, (19)
где N – количество точек информации;
F(Tik) и F(TiH) – интегральные функции, соответственно, в конце и начале i-го интервала значений показателя надежности, которые определяются по формулам для ЗНР и ЗРВ.
Если исходная информация о показателях надежности представлена в виде статистического ряда (как в нашем примере), то для определения критерия согласия χ2 составляют укрупненный статистический ряд, соблюдая правило: ny³ 4, mi³ 5. При этом следует объединить те интервалы, у которых mi< 5.
Таблица 4 – Укрупненный статистический ряд информации о доремонтных ресурсах гильз цилиндров
| Интервал, мото-ч. | 980-1478 | 1478-1976 | 1976-2474 | 2474-2972 | 2972-3470 | 3470-3968 | 3968-5462 |
| Опытная частота mi | |||||||
| Теоретическая частота mTi при ЗНР | 4,9 | 8,4 | 12,6 | 13,3 | 11,9 | 8,4 | 7,7 |
| Теоретическая частота mTi при ЗРВ | 6,02 | 11,34 | 12,6 | 13,3 | 11,2 | 7,0 | 7,0 |
Определим значения теоретических частот для ЗНР и ЗРВ.
Для ЗНР:
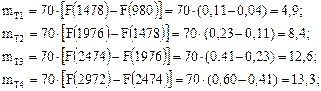
Для ЗРВ:
Определим Х2 для ЗНР:
Для ЗРВ:
По таблице Б12 приложения Б определим процент совпадения (Р%) в соответствии с полученными значениями χ2.
Определим номер строки для входа в таблицу Б12 приложения Б:
№стр=ny-k, (20)
где ny – число интервалов укрупненного статистического ряда;
k – число обязательных связей (k=3).
Для ЗРВ, так же как и для ЗНР, число обязательных связей равно трем: две связи – два параметра распределения и третья связь åР=1,0.
В нашем примере ny=7, следовательно №стр=7-3=4.
Тогда для ЗНР – Р%»10%; а для ЗРВ – Р%»21%.
Значения критерия χ2 находят в четвертой строке, а вероятность совпадения (значение Р) определяют в заглавной строке таблицы Б12 приложения Б. В случае необходимости, при несовпадении χ2 с табличными значениями, необходимо использовать метод интерполирования.
Сравнивая значения критериев согласия, приходим к окончательному выводу о том, что применительно к доремонтным ресурсам гильз цилиндров в нашем случае более приемлемым является закон распределения Вейбулла (определяется по большей вероятности совпадения Р). Выбрав окончательно в качестве теоретического закона ЗРВ, наносим на график значения f(Tдр) по серединам интервалов и F(Tдр) по концам интервалов, которые будут теоретическими дифференциальной и интегральной кривыми распределения ресурсов (см. рисунок 2).
| Рисунок 2 – Теоретическая дифференциальная (1) и теоретическая интегральная (2) кривые распределе-ния ресурсов гильз цилиндров |
