Надежность измерения социальных характеристик

Описанные выше способы построения шкал не дают полного представления о свойствах полученных оценок. Для этого необходимы дополнительные процедуры, результаты которых будем описывать в терминах ошибок измерения. Назовем это проблемой надежности измерения. Рассмотрим ее решение на пути выявления правильности измерения, его устойчивости и обоснованности.

Компоненты надежного измерения. При изучении правильности -устанавливается общая приемлемость данного способа измерения. Непосредственно понятие правильности связано с возможностью учета в результате измерения различного рода систематических ошибок. Систематические ошибки имеют некоторую стабильную природу возникновения: либо они являются постоянными, либо меняются по определенному закону.

Устойчивость характеризует степень совпадения результатов измерения при повторных применениях измерительной процедуры и описывается величиной случайной ошибки. Наиболее сложный вопрос надежности измерения — его обоснованность. Обоснованность связана с доказательством того, что измерено вполне определенное заданное свойство объекта, а не некоторое другое, более или менее на него похожее.

При установлении надежности следует иметь в виду, что в процессе измерения участвуют три составляющие: объект измерения, измеряющие средства, с помощью которых производится отображение свойств объекта на числовую систему, и субъект, производящий измерение. Предпосылки надежного измерения кроются в каждой отдельной составляющей.

Прежде всего сам объект в отношении измеряемого свойства может обладать значительной степенью неопределенности. Так, зачастую у индивида нет четкой иерархии жизненных ценностей, а следовательно, нельзя получить и абсолютно точные данные, характеризующие важность для него тех или иных явлений.

Но может быть и так, что способ получения оценки не обеспечивает максимально точных значений измеряемого свойства. Например, у респондента существует определенная иерархия ценностей, а для получения информации используется номинальная оценка с вариациями ответов от «очень важно» до «совсем неважно». Как правило, из приведенного набора все ценности помечаются ответами «очень важно», «важно», хотя реально у респондента имеется большее число уровней значимости.

Наконец, при наличии высокой точности первых двух составляющих измерения субъект, производящий измерение, допускает грубые ошибки. Например, в процессе клинического интервью, в ходе которого должна быть выявлена система Ценностей опрашиваемого, интервьюер не смог довести до респондента суть беседы, не смог добиться доброжелательного отношения к исследованию и пр.

Каждая составляющая процесса измерения может быть источником ошибки, связанной либо с устойчивостью, либо с правильностью, либо с обоснованностью. Однако, как правило, исследователь не в состоянии разделить эти ошибки по источникам их происхождения и поэтому изучает ошибки устойчивости, правильности и обоснованности всего измерительного комплекса в совокупности. При этом правильность (как отсутствие систематических ошибок): и устойчивость информации —элементарные предпосылки надежности. Наличие существенной ошибки в этом отношении уже сводит на нет проверку данных измерения на обоснованность.

В отличие от правильности и устойчивости, которые 'могут быть измерены достаточно строго и выражены в форме числового показателя, критерии обоснованности определяются либо на основе логических рассуждений, либо на основе косвенных показателей. В смежных с социологией науках, например в психологии, проблема обоснованности теста решается путем сопоставления его результатов с результатами внешнего критерия — с известной группой или с данными реального поведения. В социологии такой придем, как правило, не удается использовать, поэтому обычно применяется сравнение данных одной методики с данными других: методик или исследований, т. е. обоснованность устанавливается более косвенным путем. При этом, разумеется, не обязательно добиваться полного соответствия результатов. Достаточным будет установление общих тенденций, что зависит и от соотносительной значимости самих критериев, и от их функции в общем замысле исследования.

Правильность измерения — выявление систематических ошибок. Прежде чем приступать к изучению таких компонентов надежности, как устойчивость и обоснованность. Необходимо убедиться в правильности выбранного инструмента измерения (шкалы или, системы шкал).

Возможно, что последующие этапы окажутся излишними, если в самом начале выяснится полная неспособность данного инструмента на требуемом уровне дифференцировать изучаемую совокупность, или может оказаться, что систематически не используется какая-то часть шкалы или ее отдельная градация. Прежде всего нужно ликвидировать или уменьшить такого рода недостатки шкалы и только затем использовать ее в исследовании,

Отсутствие разброса, ответов по значениям шкалы. Попадание ответов в один, пункт свидетельствует о полной непригодности измерительного инструмента — шкалы. Такая ситуация может возникнуть или из-за «нормативного» давления в сторону общепринятого мнения; или из-за того, что градации(значения) шкалы поимею? отношения к определению данного свойства рассматриваемых объектов (нерелевантны).

Например, если все опрашиваемые респонденты согласны с утверждением «хорошо, когда работа или задание требуют универсальных знаний», нет ни одного ответа «не согласен», остается только зафиксировать этот факт, однако подобная шкала не поможет дифференцировать изучаемую совокупность по отношению респондентов» к работе.

Часто примером нерелевантности являются многие исходные шкалы методики семантического дифференциала Осгуда. Так, в частности, при изучении установок инженера в работе измерения респондентов по шкалам «мужской — женский», «горячий — холодный» и др. давали оценку только в середине шкалы, в нейтральной точке, Уточнение позволило сделать вывод, что эти шкалы, по мнению респондентов, не, имеют отношения к изучаемым установкам.

Использование части шкалы. Довольно часто - обнаруживается, что практически работает лишь какая-то часть шкалы, какой-то один из его полюсов с прилегающей более или менее обширной зоной.

Так, если респондентам для оценки предлагается шкала, имеющая положительный и. отрицательный полюса, в частности от +3 до —3, то при оценивании какой-то заведомо положительной ситуации респонденты не используют отрицательные оценки, а дифференцируют свое мнение лишь с помощью положительных. Для того чтобы вычислить значение относительной ошибки измерения, исследователь должен знать определенно, какой же метрикой пользуется респондент — всеми семью градациями шкалы или только четырьмя положительными. Так, ошибка измерения в 1 балл мало о чем говорит, если мы не знаем, какова действительная вариация мнений.

Пример ¹³. Девятнадцати испытуемым было предложено высказать отношение к трем понятиям по семи шкалам к каждому. Шкалы имели по 21 градации с крайними полюсами +10 и —10 и средней точкой 0. В целом получено 399 (19 • 3 • 7) оценок соследующим распределением:

Поскольку значения а_i< 0 использовались всего лишь 11 раз: (3 + 3 + 5) из 399, т. е. в 2,8% случаев, то возникает вопрос, действует ли отрицательная часть этой шкалы. Возможно, что попадание в эту часть шкалы — явление чисто, случайное. Проверим предположение.

Будем считать, что если вероятность попадания в конец шкалы превышает 5% при достаточно малом уровне значимости (a == 0,05 или a=0,01), то наблюдаемые попадания ответов являются случайными и соответствующая часть шкалы «не работает». Для этого границы доверительного интервала, построенного по имеющейся частоте для вероятности попадания в конец шкалы, сравним со значением 5 %. Если значение 5% оказывается выше границ этого интервала, то следует признать, что проверяемая часть шкалы «не работает».

Для расчета границ доверительного интервала воспользуемся формулами ¹⁴

Здесь т — доля попаданий в проверяемую часть шкалы; га — объем выборочной совокупности данных; Z — коэффициент доверия, соответствующий 2a (о доверительном оценивании см. с. 211).

Для рассматриваемого примера т — 0,0276; п — 399; Z_a = l,96 для а = 0,05. Подставляя эти значения в формулы, получим p_t = 0,016, p_z = 0,049. То же самое в процентах: р₁ = 1,6%; р₂ = 4,9%. Поскольку значение 5% не принадлежит интервалу (1,6%; 4,9%), то считаем, что отрицательная часть шкалы (а_i < 0) «не работает», следовательно, 21-балльная оценка функционирует лишь в области от +10 до 0.

Для вопросов, имеющих качественные градации ответов, можно применять подобное требование в отношении каждого пункта шкалы: каждый из них должен набирать не менее 5% ответов, в противном случае считаем этот пункт шкалы неработающим.

Требование 5%-го уровня наполнения в двух рассмотренных задачах не следует рассматривать как строго обязательное; в зависимости от задач исследования могут быть выдвинуты большие или меньшие значения этих уровней.

Неравномерное использование отдельных пунктов шкалы. Случается, особенно при использовании упорядоченных шкал, градации которых сопровождаются словесными описаниями, что некоторое значение переменной (признака) систематически выпадает из поля зрения респондентов, хотя соседние градации, характеризующие более низкую и более высокую степень выраженности признака, имеют существенное наполнение.

Так, если конфигурация распределения ответов на вопрос с четырьмя упорядоченными градациями такая, как на рис. 14, то, видимо, шкала неудачно сформулирована. Значительное наполнение двух соседних пунктов (1 и о) свидетельствует о «захвате» части голосов из плохо, сформулированного пункта 2. Аналогичная картина наблюдается и в том случае, когда респонденту предлагают шкалу, имеющую слишком большую дробность: будучи не в, состоянии оперировать всеми градациями шкалы, респондент выбирает лишь несколько базовых. Например, зачастую десятибалльную шкалу респонденты расценивают как некоторую модификацию пятибалльной, предполагая, что «десять» соответствует «пяти», «восемь» — «четырем», «пять» — «трем» и т. д. При этом базовые оценки используются значительно чаще, чем другие.

Для выявления указанных аномалий равномерного распределения по шкале можно предложить следующее правило: для достаточно большой доверительной вероятности (1 — a >=0,99) и, следовательно, в достаточно широких границах наполнение каждого значения не должно существенно отличаться от среднего из соседних наполнений.

Соответствующий статистический критерий таков:

Эта величина имеет хи-квадрат распределение с одной степенью свободы (df = 1).

Здесь i — номер значения признака, который подвергается анализу; п_i — наблюдаемая частота дли этого значения;

Пример. Рассмотрим случай измерения в десятибалльной шкале ряди ценностей типа «любимая работа», «материальный достаток», «здоровье» и т. д. При 45 испытуемых и 14 предложенных ценностях получены 623 оценки, распределение которых выглядит так.

Поскольку предполагается, что шкала должна «работать» равномерно, то, возможно, пункты шкалы 9, 7, 5 не удовлетворяют этому требованию.

Для оценки а_i = 9 наблюдаемая частота n₉ = 67,Г ожидаемая —

Подставим данные значения в формулу c² и получим расчетную величину c² = 22,93. Поскольку c² = 22,93>c² _кр = 6,63 (a=0,01), то следует признать различие между наблюдаемой и ожидаемой частотами значимым. Следовательно, частота 67 для оцейки а = 9 «лишком Мала но сравнению с соседними.

Аналогичные расчеты проводятся для пунктов шкалы а = 7 и а=5; частота пункта 7 (n₇= 60) не противоречит выдвинутому требованию равномерности; частота оценки 5 (n₅ = 81) слишком велика по сравнению с соседними и, таким образом, противоречит | требованию равномерности. 1

Определение грубых ошибок. В процессе измерения иногда возникают грубые ошибки, причиной которых могут быть неправильные записи исходных данных, плохие расчеты, неквалифицированное использование измерительных средств и т. п. Это проявляется в том, что в рядах измерений попадаются данные, резко отличающиеся от совокупности всех остальных значений. Чтобы выяснить, нужно ли эти значения признать грубыми ошибками, устанавливают критическую границу так, чтобы вероятность превышения ее крайними значениями была достаточно малой и соответствовала некоторому уровню значимости а. Это правило основано на том, что появление в выборке чрезмерно больших значений хотя и возможно как следствие естественной вариабельности значений, но маловероятно.

Если окажется, что какие-то крайние значения совокупности принадлежат ей с очень малой вероятностью, то такие значения, признаются грубыми ошибками и исключаются из дальнейшего рассмотрения. Выявление грубых ошибок особенно важно проводить для выборок малых, объемов: не будучи исключенными из анализа, они существенно искажают параметры выборки:

Статистический критерий t определения грубых ошибок таков, где t >t_крв качестве t выступает либо t max либо t min)¹⁵

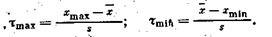
Здесь x_min и x_max являются крайними членами некоторой совокупности значений {х}.

В табл. XII, приводимой В. Ю. Урбахом¹⁶, даны критические значения t, соответствующие различным объемам выборки для доверительных уровней: a= 0,05 и a= 0,01.

Например, при выборке в 50 единиц значение t для уровня a= 0,05 будет 3,16.

Если t расчетное окажется больше t критического, то соответствующее хсчитается маловероятным и отбрасывается как грубая ошибка.

Пример. Представим, что получены распределения по признаку с такими выборочными параметрами: х=0,012; s = 0,160 (при объеме выборки n= 29 респондентов). В этом распределении крайними значениями оказались такие: x_min= 0,50; x_max =0,250. Существенное подозрение вызывает значение, равное —0,500, поскольку среднее значение этого признака близко к 0 (0,012), а вариация его значений невелика (s = 0,160).

Так как для n=29 и a=0,05 t_кр = 2,94,"то с вероятностью 0,95 можно признать, что значение признака х= — 0,500 слишком мало для данной совокупности, и поэтому является грубой ошибкой а х — 0,250 не относится к резко выделяющимся значениям.

Итак, дифференцирующая способность шкалы как первая существенная характеристика ее надежности предполагает: обеспечение достаточного разбора данных, выявление фактического использования респондентом предложенной протяженности шкалы; анализ отдельных «выпадающих» значений, исключение грубых ошибок. После того как установлена относительная приемлемость используемых шкал в указанных аспектах, следует переходить к выявлению устойчивости измерения по этой шкале.

Устойчивость измерения.

О высокой надежности шкалы можно говорить лишь в том случае, если повторные измерения при помощи одних и тех же объектов дают сходные результаты устойчивость проверяется на одной и той же выборке исследуемых объектов (респондентов). Сравнение же средних оценок разных выборок ничего не говорит об устойчивости измерения как таковом, а только лишь о репрезентативности выборок и их соответствий одной, и той же совокупности. Обычно устойчивость проверяй проведением двух последовательных замеров с определенным временным интервалом — таким, чтобы этот промежуток не был слишком велик, чтобы сказалось изменение самого объекту но не слишком май, чтобы респондент мог по памяти «подтягивать» данные второго замера к предыдущему (т. е. его протяженность зависит от (объекта изучения и колеблется от двух до трех недель).

Осуществление более двух измерений связано с трудностями организации эксперимента и накапливанием ошибок другой природы, не связанной, с устойчивостью.

Пусть х — изучаемый на устойчивость признак, а отдельные его значения— х₁, x₂…х_к. Каждый респондент l(l=1,…n) и при первом и при втором опросах получает некоторую оценку по изучаемому признаку — x¹_lи x²_lсоответственно/

Результаты двух опросов в респондентов заносятся в таблицу сопряженности (табл. 30), которая служит основой для дальнейшего изучения вопросов устойчивости. Здесь n_ij — число респондентов, выбравших в первом опросе ответ х_i и заменивших его при втором опросе на ответ x_j.

Существует традиция изучать устойчивость с помощью анализа корреляций между ответами проб I и II. Однако этот подход недостаточно эффективен, поскольку не учитывает многих аспектов устойчивости.

Остановимся на более результативных показателях.

1. Показателем абсолютной устойчивости шкалы назовем величину, показывающую долю совпадающих ответов в последовательных пробах.

Этот показатель использует не всю информацию, содержащуюся в соотношении ответов проб I и II, а базируется лишь на частотах совпадающих ответов. Однако он хорош, например, для характеристики устойчивости качественных признаков.

Для описания устойчивости количественных признаков его недостаточно, поскольку при большом числе градаций доля совпадающих ответов будет чрезвычайно мала назначение W мало информативно. Здесь пригодны показатели неустойчивости, т. е. величины ошибки, учитывающие не просто факт несовпадения ответов, а степень этого несовпадения. Ошибки рассчитываются по крайней мере для порядковых признаков.

Линейной мерой несовпадения оценок, является средняя арифметическая ошибка, показывающая средний сдвиг в ответах в расчете на одну пару последовательных наблюдений:

Здесь х¹ и х¹¹ — ответы по анализируемому вопросу L - го респондента в I и II пробах соответственно.

Пример. Пусть ответы на вопрос в пятибальной шкале для выборки 50 человек распределились, как в табл. 31.

Таким образом, в I пробе оценку «1» дали 9 респондентов, из них только трое повторили ее в пробе II, пятеро отметили «2», один дал оценку «3» и т. д.

Данный показатель использует всю информацию, содержащуюся в распределении, хорошо интерпретируется как средний сдвиг в ответах одного респондента, однако имеет определенные ограничения аналитического характера и поэтому обычно редко используется в статистических расчетах.

Средняя квадратическая ошибка для последовательных данных¹⁷ в расчете на одну пару наблюдений выглядит так:

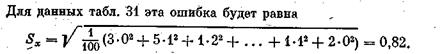
(совпадение S_x и 1AI в этом примере чисто случайное).

До сих пор речь шла об абсолютный ошибках, размер которых выражался в тех же единицах, что и сама измеряемая величина, например 0,82 балла в пятибалльной шкале. Это не позволяет сравнивать ошибки измерения разных признаков по разным шкалам. Следовательно, помимо абсолютных, нужны относительные показатели ошибок измерения.

В качестве показателя для нормирования абсолютной ошибки можно использовать максимально возможную ошибку в рассматриваемой шкале (Dmax).

Если число делений шкалы k, тогда Dmax равно разнице между крайними значениями шкалы (Xmax – Xmin), т. е. k—1, и относительная ошибка имеет вид

(здесь |D|— средняя арифметическая ошибка измерения).

Однако зачастую этот показатель «плохо работает» из-за того, что шкала не используется на всей ее протяженности. Поэтому более показательными являются относительные ошибки, рассчитанные по фактически используемой части шкалы, как было рассмотрено выше. Если число градаций в «работающей» части шкалы обозначить k', то тогда более надежной будет такая оценка ошибки:

Если в качестве абсолютной ошибки использовалась средняя квадратическая ошибка S, то показатель относительной ошибки

Пример. Допустим, что шкала имеет 7 градаций. При определении «работающей» части этой шкалы анализируется распределение полученных в I пробе оценок:

Здесь на оценки «5», «6»-, «7» приходится лишь 11 наблюдений, т. е. 2,26%. Проверка согласно критерию (формула (1)) устанавливает, что эта часть шкалы «не работает»; т. е. используются лишь градации 1, 2, 3, 4, поэтому Dmaх = 4 — 1 = 3. На основании соотношения ответов в I и II пробах находим сдвиги в ответах (ошибки). Распределение ошибок по этой шкале оказалось следующим:

измерения. Однако оценка по k также является довольно грубой и не использует всю информацию, содержащуюся в ответах I пробы ведь реально не все оценки могут дать максимальный сдвиг, а только крайние на шкале.

Оценим для приведенного распределения максимальный сдвиг по реально работающей части шкалы: только крайние значения (233, 78 + 11) могут дать сдвиг в 3 балла, 106 и 59 ответов могут дать максимальный сдвиг в 2 балла. Таким образом, возможный сдвиг для данного исходного распределения «может быть равен средней в 2,6 балла четырех балльной шкалы, т. е. фактическая ошибка еще больше: 0,6:2,6= 0,23.

Повышение устойчивости измерения. Для решения этой задачи необходимо выяснить различительные возможности пунктов: используемой шкалы, что предполагает четкую фиксацию респондентами отдельных значений: каждая оценка должна быть строго отделена от соседней. На практике это означает, что в последовательных пробах респонденты практически повторяют свои оценки. Следовательно, высокой различимости делений шкалы должна соответствовать малая ошибка.

Эту жё задачу можно описать в терминах чувствительности шкалы, которая характеризуется количеством делений, приходящихся на одну и ту же разность в значениях измеряемой величины, т. е. чем больше градаций в, шкале, тем/больше ее чувствительность. Однако чувствительность нельзя повышать простым увеличением дробности, ибо высокая чувствительность при низкой устойчивости является излишней (например, шкала в 100 баллов, а ошибка измерения ±10 баллов).

Во и при малом числе градаций, т. е. при низкой чувствительности, может быть низкая устойчивость, и тогда следует увеличить дробность шкалы. Так бывает, когда респонденту навязывают категорические ответы «да», «нет», а он предпочел бы менее жесткие оценки. И потому он выбирает в повторных испытаниях иногда «да», иногда «нет» для характеристики своего нейтрального положения.

Итак, следует найти некоторое оптимальное соотношение между чувствительностью и устойчивостью. Введём правило: использовать столько градаций в шкале, чтобы ее ошибка была меньше 0,5 балла. - _: ".

Если ошибка меньше 0,5 балла, то в последовательных опросах ответы в среднем будут совпадать. При |D| >0,5 балла ответы в последовательных опросах будут в среднем отличаться на 1 балл (и выше).

Существуют способы, «позволяющие добиться требуемой чувствительности.

Пример. В исследовании каждый испытуемый дает 8 оценок некоторым профессиональным качествам инженеров. Значение оценок варьирует от +3 до —3. Проведено два измерения. Рассмотрим суммарное распределение оценок по четырем качествам (самостоятельность, творчество, инициативность, опытность), данных тринадцати респондентов (табл. 32).

Всего в табл 32 представлено 416 пар наблюдений: 13 респондентов X 8 оценок X 4 качества. Из них в первой пробе 226 оценок имели значение «3»; во второй пробе из них только 170 были повторены, 47 оценок получили значение «2», 6 оценок — значение «1» и 3 оценки — значение «О».

Таким образом, для исходной оценки «3» средняя оценка во второй пробе стала равной

На основании этого соотношения оценок получим распределение ошибок:

Рассчитаем среднюю арифметическую ошибку çDç= 0,69. Поскольку çDç> 0,5, ищем не различающиеся градации.

Средние оценки по каждой строке сравниваем с помощью критерия Стьюдента. Если окажется, что х₁ и x_i₊₁ отличаются незначимо (t<t_крит), то далее нужно сравнивать x_i и x_i₊₁ и т. д. до значимого отличия средних (t_ti, _i₊_tзаписаны в последнем столбце табл. 32, а значимы» значения выделены).

Таким образом, оценки «3». и «2» отличаются между собой существенно, поскольку критерий Стьюдента фиксирует значимое различие между 2,70 и 2,47; оценки «2» и «1» несущественно отличаются друг от друга и т. д. Представим результаты сравнения исходных оценок при помощи схемы разбиения совокупности оценок на классы эквивалентности:

Здесь все оценки попадают в три непересекающихся класса: оценка «3» отличается от «2»; «2» и «1» не отличаются друг от друга, но отличаются от соседних оценок; последние четыре значения взаимно неразличимы.

Следовательно, респонденты различают лишь три уровня вместо семи предложенных, и шкала должна быть преобразована в трехбалльную, где высокой оценке соответствует исходная оценка в 3 балла, бредней — 2 и 1 балл; низкой — О, —1, —2, —3. Присвоим описанным уровням новые баллы — соответственно 3, 2, 1. В итоге имеем следующее соотношение оценок (табл. 33).

Это распределение характеризуется ошибкой çDç=0,43 балла, т. е. уже меньше 0,5 градации, и потому такая шкала устойчива.

В общем случае возможны два варианта соотношения исходных оценок: 1) классы неразличимости оценок неё пересекаются (например, как это было в только что рассмотренном случае);

2) классы неразличимости оценок пересекаются например так:

В первом случае можно подобрать для шкалы числовую серию, т. е. упорядоченный ряд чисел, в котором большее число характеризует более высокий уровень качества.

Во втором случае имеется полуупорядоченная система оценок, и ее можно отобразить лишь на полуупорядоченную числовую систему. В рассматриваемом примере возможно, в частности, такое числовое представление:

Там, где между исходными оценками нет существенного различия, разница между значениями числового представления (нижний ряд чисел) меньше 1; при значимом различии разница больше 1.

Однако часто желательно иметь преобразованные оценки, выраженные целыми числами. В таком случае можно предложить следующую систему понижения дробности шкалы: ближайшим исходным значениям, существенно отличающимся друг от друга, присваивают ранги последовательно I, II, III и, т. д. В рассматриваемом примере будет выглядеть так:

Для промежуточных значений, несущественно отличающихся от соседних (например, исходную оценку «2» можно отнести в любые классы — и в I, и во II), следует предложить дополнительные критерии отнесения их в один из двух соседних классов. Можно в качестве критерия использовать меру относительной близости промежуточной оценки к тому или иному соседнему классу и путем перебора всех возможных схем объединения искать схему с наименьшей ошибкой.

В конечном итоге порядок действия может быть таким. На основе данных двух последовательных проб определяем пороги различаемости градаций шкалы, В том случае, если обнаружено смешение градаций, применяют один из двух способов.

Первый способ, и итоговом варианте уменьшают дробность шкалы (например, из шкалы в 7 интервалов переходят на шкалу в 3 интервала).

Второй способ. Для предъявления респонденту сохраняют прежнюю дробность шкалы и только при обработке укрупняют соответствующие ее пункты (как это было показано выше).

Второй способ кажется предпочтительнее, поскольку, как правило, большая дробность шкал побуждает респондента и к более активной реакции. При обработке данных информацию следует перекодировать в соответствии с проведенным анализом различительной способности исходной' шкалы.

Итак, предложенные способы анализа целесообразны при отработке окончательного варианта методики. Анализ устойчивости отдельных вопросов шкалы позволяет; а) выявить плохо сформулированные вопросы, их неадекватное понимание разными респондентами; б) уточнить интерпретацию шкалы» предложенной для оценки того или иного явления, выявить более оптимальный вариант дробности значения шкалы.

Изучение устойчивости окончательного варианта методики даст представление о надежности данных (связанной устойчивостью), которые будут получены в основном исследовании.

Обоснованность измерения.

Проверка обоснованности шкалы предпринимается лишь после того, как установлены достаточные правильность и устойчивость измерения исходных данных. Как уже отмечалось, проверка обоснованности — достаточно сложный процесс я, как правило, не до конца разрешимый, И поэтому нецелесообразно сначала применять трудоемкую технику для выявления обоснованности, а после- Этого убеждаться в неприемлемости данных вследствие их низкой устойчивости.

Обоснованность данных измерения — это доказательство соответствия между тем, что измерено, и тем, что должно было быть измерено. Некоторые исследователи предпочитают исходить из так называемой наличной обоснованности, т. е. обоснованности в понятиях использованной процедуры. Например, считают, что удовлетворенность работой— это то свойство, которое содержится в /ответах -на вопрос: «Удовлетворены ли Вы работой?» В серьезном социологическом исследовании, имеющем целью проверку некоторые теоретических гипотез, такой сугубо эмпирический подход неприемлем.

Остановимся на возможных формальных подходах к выяснению уровня обоснованности методики. Их можно разделить на три группы: 1) конструирование, типологии в соответствии с целями исследования на базе нескольких признаков; 2) использование параллельных данных; 3) судейские процедуры.

Первый вариант нельзя считать формальным методом — это всего лишь некоторая схематизация логических рассуждений, начало процедуры обоснования, которая может быть на этом и закончена, а может быть подкреплена более мощными средствами.

Второй вариант требует использования по крайней мере двух источников для выявления одного и того же свойства. Обоснованность определяется степенью согласованности соответствующих данных.

В последнем случае мы полагаемся на компетентность судей, которым предлагается определить, измеряем > ли мы нужное Вам свойство или что-то иное.

Рассмотрим предложенные варианты последовательно. Конструированная типологиях Один из способов —использование контрольных вопросов, которые _в совокупности- с основными дают большее приближение к содержанию изучаемого свойства, раскрывая различные его стороны.

Например, можно определять удовлетворенность работой лобовым вопросом: «Устраивает ли вас Ваша нынешняя работа?» Комбинация его с двумя другими косвенными: «Хотите ли Вы перейти на другую работу?» и «Предположим, что Вы по каким-то причинам временно не работаете. Вернулись бы Вы на свое прежнее месте работы?» позволяет произвести более надежную дифференциацию респондентов. Типология по пяти упорядоченным группам от наиболее удовлетворенных работой до наименее удовлетворенных проводится с помощью «логического квадрата.

Обоснованность в подобного рода типологии не доказывается каким-либо формальным критерием и опирается на логические доводы.

Единственное требование, которое может быть выдвинуто при конструировании такого рода типологии,— это положительная корреляция между составляющими ее признаками. Отсутствие положительной взаимосвязи между вопросами может свидетельствовать о том, что мы не понижаем сущности измеряемого явления.

Так, попытка построить типологию самостоятельности инженера в работе на базе двух вопросов — сложность получаемых инженером заданий (плюс за сложность) и обращение его за консультациями (плюс за самостоятельное решение) — оказалась неудачной, ибо вопросы коррелировали отрицательным образом и как раз сложность задания предполагала обращение к консультациям.

Параллельные данные. Нередко целесообразно разработать два равноправных приема измерения заданного признака, что позволяет установить обоснованность методов относительно друг друга, т.е. повысить общую обоснованность путем сопоставления двух независимых результатов.

Классифицируем параллельные процедуры в зависимости от соотношения методов и исполнителей: а) несколько методов — один исполнитель. б) один метод — несколько исполнителей; в) несколько методов — несколько исполнителей.

Несколько методов — один исполнитель. Здесь один и тот же исполнитель использует два или более различных метода для измерения одного и того же свойства.

Рассмотрим различные способы использования этого метода, и прежде всего — эквивалентные шкалы. Понятие эквивалентности тесно связано здесь с психологическим явлением социальной установки. Всевозможные акты поведения, обусловленные некоторой установкой, или состояние (Предрасположенности к определенному поведений: составляют целостность (универсум) данной предрасположенности. Универсум можно описать совокупностью признаков.

Возможны равнозначные выборки признаков для описания — измерения социальной установки. Эти выборки и образуют параллельные шкалы, обеспечивая параллельную надежность.

Каждую шкалу рассматриваем как способ измерения некоторого свойства в зависимости от числа параллельных шкал имеем ряд способов измерения. В качестве исполнителя выступает респондент, дающий ответы одновременно по всем параллельным шкалам. Все ответы сортируем в зависимости от принадлежности ki шкале и таким образом получаем параллельные данные.

При обработке такого рода данных следует выяснить два момента: 1) непротиворечивость пунктов отдельной шкалы; 2) согласованность оценок по разным шкалам.

Первая проблема возникает в связи о тем, что модели ответов не представляют идеальной картины: ответы нередко, противоречат ДРУГ другу, Такая противоречивость свойственна как кумулятивным, так я некумулятивным шкалам. Поэтому встает вопрос, что принимать за истинное значение оценки респондента на данной шкале.

Вторая проблема непосредственно касается сопоставления параллельных данных,

Рассмотрим пример неудавшейся попытки повысить надежность измерения признака «удовлетворенность инженера профессией» с помощью трех параллельных порядковых шкал. Приведем две из них:

15 суждений (в порядке, обозначенном слева) предъявляются респонденту общим списком, и он должен выразить свое согласие или несогласие с каждым из них. Каждому суждению присваивается оценка, соответствующая его рангу в указанной шкале (справа). (Например, согласие с суждением 4 дает оценку «1», согласие с суждением 11 —оценку «5» и т. д.).

Рассматриваемый здесь способ предъявления суждений списком дает возможность проанализировать пункты шкалы на непротиворечивость. При использовании упорядоченных номинальных шкал обычно считается, что пункты, образующие шкалу, взаимно исключают друг друга и респондент легко, найдет тот из них, который ему подходит.

Изучение распределений ответов показывает, что респонденты выражают согласие с противоречивыми (с точки зрения исходной гипотезы) суждениями. Например, по шкале «S» 42 человека из 100 одновременно согласились с суждениями 13 и 12, т. е. с двумя противоположными суждениями.

Наличие в ответе противоречивых суждений приводит к необходимости вычислять ошибку противоречивости. Это будет разница в рангах, наиболее противоположных для данной шкалы суждений в ответе респондента.

Итак, средние ошибки, характеризующие противоречивость для рассматриваемых шкал, оказались равными

D_а=0,37; D_b=1,57

Ошибка в 1,57 балла при пятибалльной оценке, видимо, слишком велика, чтобы считать шкалу приемлемой.

Для эквивалентных шкал итоговая оценка респондента рассчитывается как суммарная (или усредненная) оценка по разным шкалам. Однако для правомерности такой процедуры необходимо установить соответствие оценок респондента по всем рассматриваемым шкалам.

В вышеприведенном примере такого соответствия не наблюдалось, что сказалось на коэффициенте корреляции r= -0,02.

Поиск эквивалентной процедуры для повышения надежности шкалы весьма утомительная и кропотливая операция. Поэтому данный прием можно рекомендовать лишь при разработке ответственных психологических тестов или методик, предназначенных для массового употребления или панельных исследований.

Один метод — несколько исполнителей. Если метод надежен, то разные исполнители дадут совпадающую информацию, но если Их результаты плохо согласуются, то либо измерения ненадежны, либо результаты отдельных исполнителей нельзя считать равноценными. В последнем случае надо установить, нельзя ли считать какую-либо группу результатов заслуживающей большего доверия. Решение этой задачи тем более важно, если предполагается, что одинаково допустимо получение информации любым из рассматриваемых методов (например, использование самооценок против оценок). Анализ параллельных данных с помощью описанных ниже процедур позволит установить правильность такого предположения.

Для количественных признаков при решении вопроса о согласованности оценок нескольких исполнителей предлагается выявить ошибки соответствия одним из приемов, рассмотренных при изучении устойчивости. Прежде всего, поскольку мы имеем здесь случай прямых групповых наблюдений, наиболее адекватной оценкой совпадения данных является средняя квадратическая ошибка.

Пусть каждый раз измерение производят два человека, и респонденту приписывается значение в виде средней (х) из двух исходных. Оценку точности такого измерения следует производить по формуле

Пример. Двое судей оценивают опытность инженера в работе по семибальной шкале. Предположим, что 13 респондентов получили такие оценки:

Итак, средняя ошибка при таком способе оценивания респондента составляет почти 1 балл. В том случае, если число измерений каждого объекта равно 3, формула для расчета ошибки будет

где n – число респондентов (объектов).

s²_i – дисперсия оценок i-го респондента.

Допустим, что рассмотренную выше совокупность из 13 респондентов оценивают не двое, а трое судей, т. е. добавляется еще одна строчка данных и следующие расчеты:

Как видно, оценивание с помощью трех лиц значительно надежнее, чем с помощью двух (соответствующие ошибки 0,69 и 0,97).

Обоснование измеряемого свойства путем определения уровня согласованности нескольких шифровальщиков — классический прием, используемый в контент-анализе документов. Этот метод, выявления надежности особенно необходим здесь, ибо, как правило, анализируемый документ не имеет в тексте четких границ измеряемого признака, референты которого расплывчаты и толкуются неоднозначно, самые детальные инструкции по шифровке все же не дают исчерпывающих указаний.

Тем же способом можно изучать совпадения оценок и самооценок. Если согласованность оценок со стороны «судей» и соответствующих самооценок респондентов будет достаточно высокой, это может означать, что методика достаточно обоснованна. Во всяком случае, одновременное использование оценок и самооценок дает возможность глубже понять сущность измеряемых признаков, уточнить их смысл.

Несколько методов и, несколько исполнителей. Одним из способов установления обоснованности измерения некоторого качества у одного и того же респондента (объекта).является фиксирование данного свойства разными исполнителями, владеющими разными.методами. Как и предыдущих случаях, здесь нельзя установить некую абсолютную, обоснованность, поэтому рассматривается лишь, обоснованность одного способа относительно другого.

Такая ситуация наблюдает, например, в случае, если руководитель ранжирует своих подчиненных по какому-то качеству а исследователь ранжирует этих же людей на основании их опроса по специально разработанной методике. Скорее всего надежность первого способа ранжирования значительно выше, и обоснованность второго метода следует проверять по его согласованности с первым.

Используя параллельные методы измерения одного и того же свойства, исследователь сталкивается с целым рядом трудностей.

Во-первых, неясно, в какой мере оба метода измеряют одно и то же качество объекта, причем, как правило, формальных критериев для проверки такой гипотезы не существует. Следовательно, необходимо прибегнуть к содержательному (логико-теоретическому) обоснованию того или иного метода.

Во-вторых, если обнаруживается, что параллельные процедуры измеряют общее свойство (данные существенно не различаются), остается вопрос о теоретико-содержательном соответствии этих процедур,.

Нельзя не признать, что сам принцип использования параллельных процедур оказывается, не формальным, а скорее содержательным принципом, и решение остается за теоретико-методологической концепцией исследования.

Именно теоретическая позиция исследователя, теоретическая обоснованность метода измерения оказываются решающими факторами при решении вопроса о предпочтительности той или иной процедуры. Такое заключение необходимо сделать по отношению к параллельным процедурам, когда ни одна из них не обладает большей достоверностью по сравнению с другой.

Метод судейства при обосновании процедур измерения. Один из широко распространенных подходов к установлению обоснованности — это использование так называемых судей. Исследователи обращаются к определенной группе людей с просьбой выступить в качестве судей или компетентных лиц. Им предлагают набор признаков, предназначенный для измерения изучаемого явления, и просят оценить правильность отнесения каждого из признаков к этому объекту. Совместная обработка мнений судей позволит присвоить признакам веса или, что то же самое, шкальные оценки в измерении изучаемого явления. В качестве набора признаков может выступить список отдельных суждений, серия предметов, совокупность обследуемых лиц и т. д.

Процедуры судейства многообразны. Способ выявления отношения признаков к измеряемому свойству определяет сущность метода. Это могут быть методы парных сравнений, ранжирования, последовательных интервалов и т. д. В каждом случае, выбирая ту или иную технику судейства, необходимо учитывать ее специфические возможности, влияющие на уровень обоснования судейских оценок.

Вопрос о том, кого следует считать судьями, достаточно дискуссионен. Судьи, выбираемые в качестве представителей изучаемой совокупности так или иначе должны представлять ее микромодель: по оценкам судей исследователь определяет, насколько адекватно будут истолкованы респондентами пункты опросной процедуры или другие обращенные к респонденту стимулы.

Однако при отборе судей возникает трудноразрешимый вопрос, каково влияние собственных установок судей на их оценки, ведь эти установки Могут существенно отличаться от установок обследуемых в отношении того же самого объекта.

Ясно, что в каждом конкретном случае следует осуществлять контроль такого рода ошибок применительно к данной выборке судей.

Так, используя мужчин и женщин в качестве судей для оценки потенциальных творческих возможностей различных занятий на досуге, нашли, что установки судей-мужчин существенно отличаются от установок судей-женщин. Более того, их установки зависят от того, увлекается ли сам судящий данным видом досуга. Например, женщины, которые занимаются рукоделием, значительно выше оценивают творческие возможности этого занятия, чем те, которые им не занимаются.

В общем виде решение, проблемы состоит в том, чтобы: а) внимательно проанализировать состав судей с точки зрения адекватности их жизненного опыта и признаков социального статуса соответствующим показателям обследуемой генеральной совокупности; б) выявить эффект индивидуальных уклонений в оценках судей относительно общего распределения оценок. Наконец, следует оценить не только качество, но и объем выборочной совокупности судей. Здесь также нет единодушия между специалистами. Рекомендуется брать то 25—30 человек, то 200—300 и более. Серьезных обоснований в обоих случаях не приводится.

Рассмотрим эту проблему на языке измерения. Поскольку судьи должны измерить некоторое свойство, которое содержится в данном признаке, процедуру судейства можно понимать таким образом: каждый судья i (1 = 1, 2,..., N), измеряя одно и то же свойство, дает признаку некоторую оценку х и помещает его в некоторый класс значений. Имея оценки N судей, получаем N измерений одного и того же признака. Если признаков k, то имеем Nk измерений. Количество судей надо поставить в прямую зависимость от вариаций их мнений и, таким образом, от однозначности измеряемого объекта.

С одной стороны, это количество определяется согласованностью: если согласованность мнений судей достаточно высокая и соответственно ошибка измерения мала, численность судей может быть небольшой. Нужно задать значение допустимой ошибки и на основании ее рассчитать требуемый объем выборки.

При обнаружении полной неопределенности объекта, т. е. в случае, когда мнения судей распределятся равномерно по всем категориям оценки, никакое увеличение объема выборки судей не спасет ситуацию и не выведет объект из состояния неопределенности.

С другой стороны, количество измерений и соответственно число судей должны быть целесообразными. Очевидно, что 1000 судей дадут более надежные данные, но разумнее ограничиться меньшим количеством, особенно если требования к точности измерения являются не слишком высокими.

Здесь возникает проблема точности (устойчивости) измерения. Рассмотрим с этой точки зрения принципиально разные варианты судейства:

1) производится классификация состояний объекта (сам объект имеет качественные градации);

2) находится количественная оценка изменяющихся состояний объекта, представляющих собой континуум.

В первом случае при определении объема выборки судей необходимо задать некоторый уровень определенности в их мнениях, т. е. энтропия распределения оценок должна быть не выше некоторого порогового значения. Во втором задается уровень допустимой ошибки. Далее возникает вопрос о численности градаций в судейских оценках, что относится к чувствительности любой измерительной процедуры. В общем случае речь идет не о чем ином, как о чувствительности измерения, зависящей и от изменчивости объекта, и от устойчивости инструмента измерения. Основной способ определения дробности судейских оценок — выявление их устойчивости путем двух последовательных (современным интервалом) судейств по единой процедуре. Эта операция уже рассматривалась выше в разделе об устойчивости.

Если объект достаточно не определен, то большое число градаций только внесет дополнительные помехи в работу судей и не принесет более точной информации. Нужно выявить устойчивость судейских мнений с помощью повторной пробы и соответственно сузить число градаций.

Выбор того или иного конкретного способа, метода или техники проверки на обоснованность зависит от многих обстоятельств.

Прежде всего следует четко установить, возможны ли какие-то существенные отклонения от запланированного предмета измерения. Как правило, интерпретация полученных данных вследствие различных погрешностей измерения не отвечает полностью эмпирической интерпретации понятий или свойств, которыми, согласно гипотезе, обладает этот объект. Бели программа исследования ставит чрезвычайно жесткие рамки следует использовать не один, а несколько приемов проверки данных на обоснованность, с тем чтобы четко определить границы достоверности заключения по гипотезе. Если же она не столь жестко ограничивает содержание объекта, уточнение уровня обоснованности поможет интерпретировать данные в несколько иных направлениях в соответствии с результатами проверки на обоснованность исходного измерения.

Во-вторых, нужно иметь в виду, что уровни устойчивости и обоснованности данных тесно взаимосвязаны. Неустойчивая информация уже в силу недостаточной надежности при этому критерию не требует, слишком строгой проверки на обоснованность. Следует обеспечить достаточную устойчивость и уже затем принять соответствующие меры для уточнения границ интерпретации данных

Наконец, надо сказать, что для оперативных Исследований, программа которых разработана лишь в общем виде: (т. е, имеется скорее общий набросок логики исследования, общий замысел), можно ограничиться проверкой данных на устойчивость, используя эту информацию. Для некоторых, хотя бы гипотетических, суждений относительно обоснованности.

Выбор конкретной Техники проверки данных на обоснованность— задача скорее содержательная, чем формальная. Мы показали, как решается эта задача в зависимости от особенностей методики, подлежащей проверке на обоснованность, того места, которое она занимает в рамках всего исследования, и, главное, в соответствии со спецификой объекта измерения.

Многочисленные эксперименты по выявлению уровня надежности исходной информации, в частности рассмотренные в этой главе, позволяют заключить, что в процессе отработки инструментов измерения со стороны их надежности целесообразна следующая последовательность основных этапов работы:

1. Предварительный контроль обоснованности методов измерения первичных, данных на стадии проб методики. Здесь проверяется, насколько - информация отвечает своему назначению по существу и каковы пределы последующей интерпретации данных. Для этой цели достаточны небольшие выборки в 10-20 наблюдений с последующей корректировкой структуры методики.

2. Пилотаж методики и тщательная проверка устойчивости исходных данных, в особенности итоговых показателей, индексов, многомерных шкал и т. п. На этом этапе нужна выборка не менее 100 человек, представляющая микромодель реальной совокупности обследуемых с учетом представительства по существенным характеристикам объекта исследования.

3. В период общего пилотажа осуществляются все необходимые операции, относящиеся к проверке, уровня обоснованности. Результаты анализа данных генерального пилотажа приводят к усовершенствованию методики, к доработке всех ее деталей и в итоге — к- получению окончательного варианта методики для основного исследования.

4. В начале основного исследования желательно провести проверку используемого варианта методики на устойчивость с тем, чтобы рассчитать точные показатели ее устойчивости. Доследующее уточнение границ обоснованности проходит через весь анализ самого исследования.

Литература для дополнительного чтения

Аванесов В. С. Тесты в социологическом исследовании. М.: Наука, 1982. 199 с.

Бородкин Ф. М., Маркин Б. Г. Эмпирические, описания в социологии.— В кн.: Математика и социология. Новосибирск: Наука. Сиб. отд-ние, 1972, с. 3—41

Воронов Ю. П., Ершова Н. П. Общие принципы социологического измерения.— В кн.: Намерение и моделирование в социологии. Новосибирск: Наука. Сиб. отд-ние, 1969, с. 3—15.

Грин Ф. Б. Измерение установки.— В кн.: Математические методы в. современной буржуазной социологии. М.: Прогресс, 1966, с. 227—287.

Докторов Б. 3. О надежности измерения в социологическом исследовании. Л.: Наука, 1979. 128 с.

Жуков Ю. М. Применение шкалирования в социально-психологических исследованиях.— В кн.: Методология и методы социальной психологии. М.: Наука, 1977, с. 126—135.

Зайцева М. Л. Методы шкалирования при измерении установки.— В кн.: Социальные исследования. М.: Наука, 1970, вып. 5, с. 220—242.

Клигер С. А., Косолапое М. С., Толстова Ю. И. Шкалирование при сборе и анализе социологической информации. М.: Наука, 1978. 112 с.

Лазарсфельд П. Ф. Измерение в социологии.— В кн.: Американская социология: Перспективы, проблемы, методы. М.: Прогресс, 1972, с. 134—149.

Осипов Г. В.. Андреев Э. П. Методы измерения в социологии. М.: Наука, 1977. 183 с.

Процесс социального исследования. Прогресс. 1975, разд. 1,4,2. Саганенко Г. И. социологическая информация: Статистическая оценка надежности исходных данных социологического исследования. Л.: Наука, 1979. 142с.

Статистическое измерение качественных характеристик. М.: Статистика, 1972.. 173 с.

Суппес П. Зинес Дж. Основы теории измерений.— В кн.: Психологические измерения. М.: Мир, 1967, с. 9—110.

Раздел третий