Графическая интерпретация эмпирических зависимостей

Частотные распределения изображаются также в виде диаграмм и графиков. Главным достоинством графического изображения яв­ляется его наглядность.

Графическая интерпретация эмпирических зависимостей осно­вана на знании технических правил построения рядов, типов и свойств теоретических распределений. Здесь мы рассмотрим графика вариационных рядов: гистограмму, полигон и кумуляту распределения.

Гистограмма.

Гистограмма — это графическое изображение интервального ряда. По оси абсцисс откладывают границы интервалов, на которых строят прямоугольники с высотой, пропорциональной плотностям распределения соответствующих интервалов (пропор­циональной числу единиц совокупности, приходящейся на единицу длины интервала). При равных интервалах плотности распределения пропорциональны частотам, которые и откладываются по оси ординат (рис. 1, табл. 2).

На гистограмме общее число лиц в каждой категории выражает­ся площадью соответствующего прямоугольника, а общая площадь равна численности совокупности (так как гистограмма на рис. 1 строится по относительным частотам, то площадь равна единице (100%). Поэтому для интервалов 4—6, 6—8, 8—10 в табл. 2, которые в 2 раза больше предыдущих, нужно брать высоты прямоугольников в 2 раза меньшие. При нанесении на графикепоследне­го открытого интервала

 

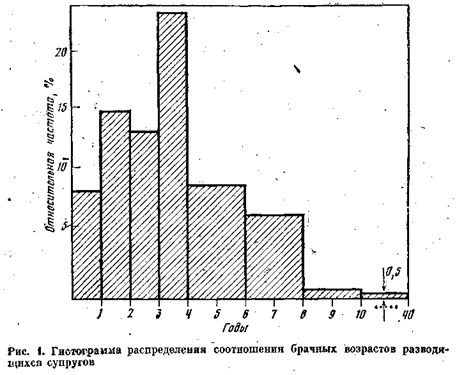
«10 лет и более» условно будем считать верхней его границей 40 лет. Тогда ширина интервала равна 30го­дам, а плотность распределения — около 0,5% (15,7: 30 ~ 0,5).

Полигон распределения.

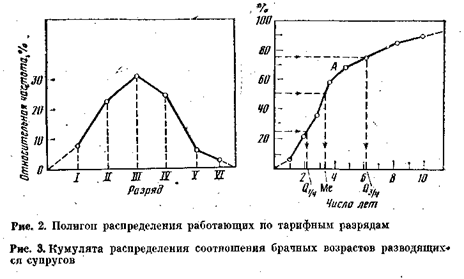
Для построения полигона величина при­знака откладывается на оси абсцисс, а частоты или относительные частоты — на оси ординат. Из точек, соответствующих значениям признака, восстанавливаются перпендикуляры, равные по высоте частотам. Вершины перпендикуляров соединяются прямыми ли­ниями.

Для интервального ряда ординаты, пропорциональные частоте (или относительной частоте) интервала, восстанавливаются перпен­дикулярно оси абсцисс в точке, соответствующей середине данного интервала.

Следующие данные распределения рабочих в возрасте до 24 лет по тарифным разрядам (высококвалифицированные рабочие сельхоз-машиностроения)¹⁵ дают возможность построить полигон распределе­ния (рис. 2):

 

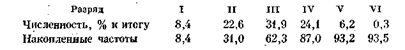
Условно принято крайние ординаты признака соединять с серединами примыкающих интервалов (на рис. 2 эти замыкающие линии нанесены пунктиром). Однако для распределения, где концентрация событий увеличивается на концах полигона, такое изображение мо­жет привести к ложным представлениям о существе явления.

Кумулята.

Для графического изображения вариационных рядов используются также кумулятивные кривые. При построении кумуляты, как и гистограммы, на оси абсцисс откладываются границы интервалов (либо значения дискретного признака), а на оси орди­нат — накопленные частоты (либо относительные частоты), соответ­ствующие верхним границам интервалов. Таким образом, отличие кумуляты от гистограммы в том, что на графике кумуляты столби­ки, пропорциональные частотам, последовательно накладываются один на другой, так что высота последнего столбика является сум­мой высот столбиков гистограммы.

Кумулята округляет индивидуальные значения признака в пре­делах интервала и представляет собой возрастающую ломаную линию.

Кумулята позволяет быстро определить процент лиц, находящихся ниже или выше заданной величины признака. Например, по данным табл. 3, процент семейств, в которых муж старше cyпруги не более чем на 5 лет, равен 65 (рис. 3, точка А).