Задачи, приводящие к дифференциальным уравнениям. Понятие о дифференциальных уравнениях первого и второго порядка. Задача Коши. Дифференциальные уравнения с разделяющимися переменными. Линейные дифференциальные уравнения первого порядка. Простейшие дифференциальные уравнения второго порядка. Однородные линейные дифференциальные уравнения первого порядка с постоянными коэффициентами.
В результате изучения темы студент должен:
знать:
· определение дифференциального уравнения;
· определение общего и частного решений дифференциальных уравнений, их геометрической интеграции;
· методы решения дифференциальных уравнений первого порядка (с разделяющими переменными, линейные) и второго порядка (простейшие; линейные однородные с постоянными коэффициентами);
уметь:
· решать несложные дифференциальные уравнения первого и второго порядков;
Рекомендуемая литература:
Л 1 ч.2, Л3 ч.1, Л4, Л6
Вопросы для самоконтроля:
1. Может ли дифференциальное уравнение 
иметь конечное число решений?
2. Могут ли интегральные кривые дифференциального уравнения пересекаться?
3. Является ли дифференциальное уравнение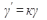 
: 1) уравнением с разделяющимися переменными; 2) линейным уравнением?
4. Должно ли дифференциальное уравнение второго порядка содержать: 1)вторую производную функции; 2) первую производную; 3) искомую функцию; 4)независимую переменную в явном виде?
5. Известно, что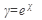 
и 
являются решениями уравнения 
. Можно ли утверждать, что 
- множество всех решений данного уравнения?
Тема 4. Ряды
Числовые ряды. Сходимость, расходимость числовых рядов. Признаки сходимости Даламбера, Коши. Знакочередующие ряды, признак Лейбница. Знакопеременные ряды. Абсолютная и условная сходимость. Функциональные ряды. Степенные ряды. Разложение элементарных функций в ряд Тейлора и Маклорена. Ряды Фуры.
В результате изучения темы студент должен
знать:
· определение числовых и функциональных рядов;
· необходимый признак сходимости рядов;
· признаки сходимости Даламбера, Коши, Лейбница;
· основные разложения элементарных функций в ряд Маклорена;
· определение ряда Фурье;
уметь:
· определять сходимость числовых рядов по признакам Даламбера, Коши, Лейбница:
· находить радиус и интервал сходимости степенных рядов;
· раскладывать элементарные функции в ряд Маклорена;
· раскладывать функцию в ряд Фурье;
Рекомендуемая литература:
Л3 ч. 2, Л4, Л6
Вопросы для самоконтроля:
1. Что такое числовой ряд, его члены, частичные суммы?
2. Что такое остаточный ряд? Как связана его сходимость со сходимостью исходного ряда?
3. В чем состоит необходимый признак сходимости ряда? Какие из приведенных ниже утверждений справедливы, а какие нет? Дайте обоснования своим ответам.
а) Если ряд сходится, то его общий член стремится к нулю.
б) Если общий член ряда стремится к нулю, то ряд сходится.
в) Если ряд расходится, то его общий член не стремится к нулю.
г) Если общий член ряда не стремится к нулю, то ряд расходится.
4. Что такое функциональный ряд? Его область определения? Область сходимости?
5. Напишите формулы для разложения в степенные ряды функций ln 
, arctgx, sin, cos и ех. При каких значениях 
справедливы эти формулы?
