Базой для изучения и освоения материала по дисциплине должны стать знания и умения,, полученные в средней школе.
Студент-заочник, приступая к самостоятельному изучению дисциплины, должен подробно ознакомиться с программой и обеспечить себя необходимыми учебниками. Проработку материала необходимо вести в последовательности, которая предусмотрена данной программой и методическими указаниями. Изучаемый материал следует детально проработать по учебнику, законспектировать основные положения, составить ответы на вопросы, помещенные в конце настоящего пособия.
По всем неясным вопросам, которые могут возникнуть при изучении дисциплины, студенты смогут обратиться за консультацией к преподавателю.
Программа
Тема 1. Комплексные числа
Понятие комплексного числа. Геометрическая интерпретация. Алгебраическая, тригонометрическая, показательная формы комплексного числа. Переход от одной формы к другой. Действия над комплексными числами в различных формах.
В результате изучения темы студент должен:
знать:
· запись комплексного числа в алгебраической, тригонометрической, показательной формах;
· геометрическую интерпретацию комплексного числа;
· по каким правилам производятся действия над комплексными числами;
уметь:
· строить комплексное число;
· различать комплексное число в разных формах;
· выполнять действия с комплексными числами;
· находить модуль и аргумент комплексного числа;
· переходить от одной формы комплексного числа к другой.
Рекомендуемая литература:
Л.1, ч.2; Л. 3,ч1; Л.4;Л.6
Вопросы для самоконтроля:
1.Что означает каждое из следующих утверждений:
а) комплексное число а+bi равно нулю;
б) комплексное число а+bi не равно нулю;
в) два комплексных числа а+bi и с+di не равны друг другу?
2. При каком условии сумма двух комплексных чисел есть:
а) действительное число?
б) чисто мнимое число?
3. Какое число сопряженное с 
?
4. В какой четверти координатной плоскости расположены точки, изображающие числа 2+7i; 5-i; -3+2i; -1-i?
5. Приведите пример комплексных чисел, которым соответствуют два перпендикулярных вектора.
6. Чему равен аргумент: а) чисто мнимого числа; б)любого отрицательного числа; в) любого положительного числа; г) нуля?
7. Число z= 
можно выразить через тригонометрические функции следующим образом:
а) 
б) 
в)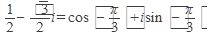 
г) 
д) 
Какой из этих записей будет тригонометрической формой числа?
8. Вычислить:1) /cos 4+ i sin4 /; 2) /е i 
/
9. Какие из следующих выражений представляют собой показательную форму комплексного числа: 2е 
; -2е i ;
2е - i ; iе ; еi ; 3е i 
?
10. Как изменяются модуль и аргумент комплексного числа в результате умножения этого числа на: а) i; б) –i; в) 2i; г) -3i; д) 4 е) 5?
