В снабженческой, производственной и распределительной логистиках широко используются методы прогнозирования, поскольку значения прогнозных оценок развития анализируемых процессов или явлений являются основой принятия управленческих решений при оперативном, тактическом и стратегическом планировании. Очевидно также, что точность и надежность прогноза определяет эффективность реализации различных логистических операций и функций – от оценки вероятности дефицита продукции на складе до выбора стратегии развития фирмы.
Теория прогнозирования включает анализ объекта прогнозирования; методы прогнозирования, подразделяющиеся на математические (формализованные) и экспертные (интуитивные); системы прогнозирования, в частности непрерывного, при котором за счет мониторинга осуществляется корректировка прогнозов в процессе функционирования объекта.
Одним из основных классификационных признаков является также период прогноза, при этом большинство авторов выделяют три вида прогнозов: краткосрочный, среднесрочный и долгосрочный. Естественно, что временные интервалы прогнозов зависят от природы объекта, т. е. изучаемой области деятельности. Так, при рассмотрении технико-экономических показателей деятельности фирм период краткосрочного прогноза не превышает 1 года, среднесрочного прогноза – от 1 до 5 лет, долгосрочного – свыше 5 лет.
Математические методы прогнозирования подразделяются на три группы:
- симплексные (простые) методы экстраполяции по временным рядам;
- статистические методы, включающие корреляционный и регрессионный анализ и др.;
- комбинированные методы, представляющие собой синтез различных вариантов прогнозов.
Прогнозы I типа (в «узком» смысле):
- осуществляются с применением симплексных или статистических методов на основе временных рядов;
- число значимых переменных включают от 1 до 3 параметров, т. е, по масштабности они относятся к сублокальным прогнозам;
- при использовании одного параметра, например, времени, такие прогнозы считаются сверхпростыми, при двух-трех взаимосвязанных параметрах – сложными;
- по степени информационной обеспеченности периода ретроспекции прогнозы I типа могут быть отнесены к объектам с полным информационным обеспечением.
Для повышения точности и достоверности прогнозных оценок I типа целесообразно использование комбинированных методов, при этом желательно использование большого количества вариантов прогноза, рассчитанных на основе различных подходов или альтернативных источников информации.
Прогноз II типа (в «широком» смысле) подразумевает, что исходные данные для получения оценок определяются с использованием опережающих методов прогнозирования: «патентного», публикационного и др. Как правило, прогнозы II типа используются для долгосрочного прогнозирования и разбиваются на два этапа: первый – получение прогнозных оценок основных факторов; второй – собственно прогноз развития процесса или явления. Учитывая объективную сложность и трудоемкость выполнения прогнозов II типа, можно констатировать, что наибольшее распространение получили методы прогнозирования I типа.
Наиболее часто для прогнозирования I типа используется метод экстраполяции. В общем случае модель прогноза включает три составляющие (рис. 3.4.1) и записывается в виде: (1.1)
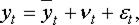
где yt – прогнозные значения временного ряда;
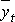– среднее значение прогноза (тренд);
vt – составляющая прогноза, отражающая сезонные колебания (сезонная волна);
εt – случайная величина отклонения прогноза.
Рис.11.1. Прогнозирование на основе временных рядов:
1 – экспериментальные данные на интервале наблюдения (A);
2 – тренд; 3 – тренд и сезонная волна;
4 – значение точечного прогноза на интервале упреждения (B);
5 – интервальный прогноз
В частных случаях количество составляющих модели меньше, например, только 
и vt.
Подробно вопросы прогнозирования с использованием методов экстраполяции изложены в ряде работ, но ввиду отсутствия общепринятого алгоритма обработки временных рядов может быть предложена следующая последовательность расчета:
1). На основе значений временного ряда на предпрогнозном периоде (интервале наблюдения) с использованием метода наименьших квадратов определяются коэффициенты уравнения тренда yt, видом которого задаются. Обычно для описания тренда используются полиномы различных порядков, экспоненциальные, степенные функции и т. п.
2). Для исследования сезонной волны значения тренда исключаются из исходного временного ряда. При наличии сезонной волны определяют коэффициенты уравнения, выбранного для аппроксимации vt.
3) Случайные величины отклонения εt определяются после исключения из временного ряда значений тренда и сезонной волны на предпрогнозном периоде. Как правило, для описания случайной величины εt используется нормальный закон распределения.
4). Для повышения точности прогноза применяются различные методы (дисконтирование, адаптация и др.). Наибольшее распространение в практике расчетов получил метод экспоненциального сглаживания, позволяющий повысить значимость последних уровней временного ряда по сравнению с начальными.
Примеры прогноза текущего запаса на складе. Рассмотрим применение методов прогнозирования на основе данных расхода деталей на складе. В табл. 11.1 приведены три реализации текущего расхода; для каждой реализации даны величины расхода за день характеристики, представляющие собой расход деталей со склада за соответствующий цикл.
Таблица 11.1
Динамика спроса в течение трех циклов расхода запасов
| 1 й цикл | 2 й цикл | 3 й цикл | ||||||
| День | Спрос, ед. | Всего с начала цикла | День | Спрос, ед. | Всего с начала цикла | День | Спрос, ед. | Всего с начала цикла |
| * | ||||||||
| * |
Проиллюстрируем возможные варианты прогнозов для одной реализации.
Пример 1. Воспользуемся первой реализацией. Допустим, что нам известны значения расхода деталей со склада за пять дней работы (табл. 11.2).
Таблица 11.2
Исходные данные и результаты расчета коэффициентов уравнения (11.2) при N=5
| ti, дн. | yi, ед. |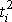 
| yiti | Прогноз yi* | (yt–yi)2 |
Суммы 
| 
| 
| 
| 
|
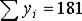
* Значения округлены
Выберем уравнение тренда yt в виде линейной зависимости:
(11.2)
Расчет коэффициентов уравнения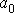 
и 
производится по формулам, полученных на основе метода наименьших квадратов:
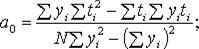(11.3)
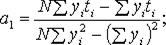(11.4)
Находим: a0 = 45,2, a1 = –3,0. Таким образом, уравнение прогноза пишется в виде:
(11.5)
Для оценки границ интервального прогноза необходимо рассчитать среднее квадратичное отклонение σt:
(11.6)
Подставляя значения в формулу, находим σt:
(11.7)
На основании полученных зависимостей yt и σt рассчитываются прогнозные оценки:
среднего времени расхода текущего запаса 
;
страхового запаса yc с заданной доверительной вероятностью Р.
Расчет прогнозной величины среднего времени расхода производится по формуле
(11.8)
Приняв yt = 0, находим:
Для расчета страхового запаса воспользуемся формулой:
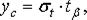(11.9)
где σt – среднее квадратичное отклонение,
tβ – параметр нормального закона распределения, соответствующий доверительной вероятности β.
Параметр tβ определяет для нормального закона число средних квадратических отклонений, которые нужно отложить от центра рассеивания (влево и вправо) для того, чтобы вероятность попадания в полученный участок была равна β.
В нашем случае доверительные интервалы откладывают вверх и вниз от среднего значения уt..
В табл. 11.3 приведены наиболее часто встречающиеся в практических расчетах значения вероятности β и параметра tβ для нормального закона распределения.
Таблица 11.3
Доверительная вероятность β и параметр tβ нормального закона распределения
| β | tβ | β | tβ |
| 0,80 | 1,282 | 0,92 | 1,750 |
| 0,82 | 1,340 | 0,94 | 1,880 |
| 0,84 | 1,404 | 0,95 | 1,960 |
| 0,86 | 1,475 | 0,96 | 2,053 |
| 0,88 | 1,554 | 0,98 | 2,325 |
| 0,90 | 1,643 | 0,99 | 2,576 |
| 0,91 | 1,694 | 0,999 | 3,290 |
Страховой запас рассчитывается так же, как и границы интервального прогноза. Для рассматриваемого примера при доверительной вероятности β=0,9 находим по табл. 3.4.3 tβ = 1,643. Тогда величина страхового запаса составит:
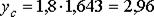
Примем yc=3,0.
На рис. 11.2 приведены границы интервального прогноза при β = 0,9.
Рис. 11.2. Прогноз текущего расхода деталей на складе (N = 5):
1 – исходные данные; 2 – уравнение тренда;
3, 3' – границы интервального прогноза; 4 – время расхода запаса
Рассчитанное значение страхового запаса соответствует только одному дню наступления дефицита, а именно согласно прогнозу T = 15. Для учета возможных нарушений срока поставки необходимо также при расчете страхового запаса оценить влияние задержки, связанной с выполнением заказа, в частности с транспортировкой.
К сожалению, по одной реализации невозможно оценить вероятностный характер длительности функциональных циклов поставки. Однако можно предположить, что выявленная тенденция расхода запаса сохранится. В этом случае для оценки прогнозной величины страхового запаса можно воспользоваться формулой
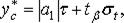(11.10)
где τ – параметр, характеризующий количество дней задержки поставки заказа.
Рассчитаем величину страхового запаса при условии задержки на один день по сравнению с прогнозной оценкой T = 15 дней, т. е. на 16-й день:
Аналогично, при τ = 2 (17 день)
Для оценки вероятности отсутствия дефицита допускается, что отклонения ежедневного расхода деталей от среднего значения (тренда) подчиняются нормальному закону распределения. Тогда, пользуясь уравнением функции нормального закона, определяют вероятность отсутствия дефицита:
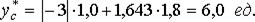(11.11)
где yt – уравнение тренда;
σ – среднее квадратическое отклонение.
В табл. 11.4 приведен ряд значений функции Ф(х) и Р(х).
Таблица 11.4
Значения нормальной функции распределения Ф(х), вероятности Р(х) и параметра x
| x | Ф(х) | Р(х) | x | Ф(х) | Р(х) |
| 0,00 | 0,50 | 0,50 | -1,280 | 0,10 | 0,90 |
| -0,125 | 0,45 | 0,55 | -1,405 | 0,08 | 0,92 |
| -0,253 | 0,40 | 0,60 | -1,555 | 0,06 | 0,94 |
| -0385 | 0,35 | 0,65 | -1,645 | 0,05 | 0,95 |
| -0,525 | 0,30 | 0,70 | -1,75 | 0,04 | 0,96 |
| -0,675 | 0,25 | 0,75 | -2,05 | 0,02 | 0,98 |
| -0,842 | 0,20 | 0,80 | -2,30 | 0,01 | 0,99 |
| -1,037 | 0,15 | 0,85 | -3,10 | 0,001 | 0,999 |
Появление дефицита означает, что текущая величина запаса на складе равна нулю, т. е. у = 0.
Для определения вероятности отсутствия дефицита необходимо:
1. рассчитать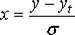 
,
2. по табл. 11.4 с помощью х найти Р(х).
Для рассматриваемого примера рассчитаем вероятности отсутствия дефицита деталей на складе на 13-й, 14-й и 15-й дни. Так, для T = 13 получаем:
и
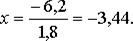
По табл. 11.4 находим РТ=13 > 0,999, т. е, вероятность отсутствия дефицита ничтожно мала.
Аналогично, для T = 14 получим yТ=14 = 3,2, x = –1,78, и вероятность отсутствия дефицита РТ=14 = 0,95.
Наконец, для T = 15 вероятность отсутствия дефицита Р = 0,5.
Следует подчеркнуть, что так же, как при оценке прогнозной величины страхового запаса, определение вероятности отсутствия дефицита по одной реализации справедливо только при строгом соблюдении сроков поставки. Если они не соблюдаются, то расчет должен проводиться с учетом рассеивания длительности функциональных циклов поставки.
В заключение определим ошибку прогноза среднего времени Т: 
(11.12)
где Tф, Tп – соответственно фактическая и прогнозная продолжительность цикла, дн.
Получим:
Ошибка прогноза велика, но это закономерно, так как нарушено одно из эмпирических правил экстраполяционного прогнозирования: между предпрогнозным периодом t и периодом упреждения (прогноза) τ = T – t должно соблюдаться соотношение:
(11.13)
При T = 5 допустимая величина времени прогноза:
Следовательно, величина надежного прогноза соответствует T ≈ 7 дн. и период упреждения составляет τ = 2 дн.
Пример 2. Считается, что средняя длина функционального цикла расхода запасов составляет T = 10 дн. Тогда t = 7,5 дн.
Увеличим длину динамического ряда до N = 7 (рис. 11.3).
Рис. 11.3. Прогноз текущего расхода деталей на складе (N = 7):
1 – исходные данные; 2 – уравнение тренда;
3, 3' – границы интервального прогноза; 4 – время расхода запаса
Выполним расчеты аналогично примеру 1, полученные данные занесем в табл. 11.5.
Исходные данные и результаты расчета коэффициентов уравнения тренда при N=7
| ti | yi |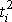
| yiti | yi | (yt–yi)2 |
| 43,1 | 4,41 | ||||
| 39,2 | 0,04 | ||||
| 35,3 | 7,29 | ||||
| 31,4 | 12,96 | ||||
| 27,6 | 0,25 | ||||
| 23,6 | 0,36 | ||||
| 19,7 | 0,49 | ||||
Суммы
| 
| 
| 
| 
|
, 
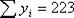
Получим уравнение тренда:
Соответственно, 
Рассчитаем среднее прогнозное время расхода запаса со склада
и ошибку прогноза:
Рассчитаем величину страхового запаса yc для 12-го, 13-го и 14-го дней. Примем β = 0,95, т. е, tβ = 1,96. Тогда:
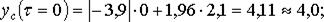
Определим вероятность дефицита на складе на 10-й день. Находим
;
по табл. 11.4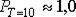 
, т.е. наличие дефицита маловероятно. Аналогично, для 
для 
.
В заключение можно сделать следующее замечание: рассчитанные величины среднего запаса получены при условии, что наблюдающая величина дефицита и вариация ежедневного расхода – независимые величины. Несомненно, это допущение требует проверки.
Комбинированный прогноз. На формирование стратегии автотранспортного предприятия (АТП) на рынке влияют факторы как внешней, так и внутренней среды, в том числе определяющие состояние спроса на услуги. Основным является вопрос о потенциальных возможностях предприятия, определяемых технико-технологическими и организационно-финансовыми факторами среды. Принципиальное различие между предъявляемыми к перевозке грузами (или спросом) и провозными возможностями АТП состоит в том, что первое следует отнести к условиям внешней среды, т. е. «природе», состояние которой формируется под действием большого количества факторов и в подавляющем большинстве случаев не зависит от транспортной политики конкретного АТП (если рассматриваемое предприятие не является монополистом в данном сегменте рынка транспортных услуг), а второе определяется политикой и тактикой действий предприятия, не имея случайного характера, а, скорее, подчиняясь неким внутренним закономерностям. Таким образом, под влиянием случайных факторов объем перевозок представляет собой случайную величину, подчиняющуюся определенному закону или функции распределения F(Q). Введение функции распределения для описания состояния «природы» позволяет, согласно теории статистических решений, использовать вероятностные критерии принятия решений в условиях риска.
Что касается состояния АТП, то оно может быть представлено в виде различных стратегий Ai, каждая из которых количественно характеризуется числом автомобилей Ni и их провозными возможностями Wi.
Указанные стратегии Ai, являются дискретными величинами, если используется число автомобилей N, или непрерывными за счет варьирования показателей, входящих в расчет производительности автомобиля Wi.
Связь между Ai стратегией и объемом перевозок Qi определяется в виде матрицы (табл. 11.6), элементы которой (aij) отражают «выигрыш», получаемый АТП при выборе i-й стратегии.
Матрица возможных стратегий Ai АТП при различных объемах перевозок Qj («состояния природы») Таблица 11.6
| Стратегия АТП | Объëм перевозок | |||||
| Q1 | Q2 | ... | Qj | ... | Qn | |
| A1 | a11 | a12 | ... | a1j | ... | a1n |
| A2 | a21 | a22 | ... | a2j | ... | a2n |
| ... | ... | ... | ... | ... | ... | ... |
| Ai | ai1 | ai2 | ... | aij | ... | ain |
| ... | ... | ... | ... | ... | ... | ... |
| Am | am1 | am2 | ... | am | ... | amn |
В ряде работ, где предпринимались попытки использования теории статистических решений для конкретных хозяйственных объектов, в качестве элемента матрицы aij – «выигрыша» – использовались условные величины. В качестве «выигрыша» могут быть использованы различные экономические показатели: доход, прибыль и другие, а также показатели, способствующие усилению конкурентных или рыночных позиций, усилению влияния на клиентуру и укреплению имиджа предприятия, улучшению качества производимых услуг.
Возможны три соотношения между объемом перевозок Qi и стратегией предприятия А. Первое –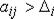 
– состояние «выигрыша»; второе – 
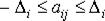– нейтральное состояние; третье – 
– состояние «проигрыша». Величина 
– вероятностное отклонение за счет случайного характера величин, определяющих значение элементов матрицы. Теоретически возможен вариант, когда области значений aij будут расположены иным образом, чем это показано на рис. 11.4.
Рис. 11.4. Распределение на различные области матрицы стратегий АТП: 1 – «выигрыш», 2 – нейтральное состояние, 3 – «проигрыш»
В частности, введение оценки «упущенной выгоды» может изменить границы областей 1-3. Считается, что наилучшей стратегией A = Ai является та, при которой показатель Ai обращается в максимум:
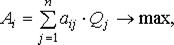(11.14)
где Qj = F(Qj) – вероятность j-го состояния «природы».
Таким образом, оптимальная стратегия АТП может быть определена при наличии F(Qj) и матрицы стратегий aij.
Рассмотрим возможные варианты расчета F(Qj). Традиционно для количественной оценки прогноза Qj, используется метод экстраполяции по динамическим рядам с использованием полиномов различной степени.
Результаты прогноза представляются в виде среднего значения Q и дисперсии DQ, по которым определяется вид функции распределения F(Qj). Далее c использованием условия максимизации Ai выбираем стратегию АТП.
Основная трудность использования вышеописанной методики – это невысокая точность прогноза, Повышение точности может быть достигнуто за счет комбинированных методов прогноза, предусматривающих синтез двух и более прогнозных вариантов.
Каждый метод прогнозирования обладает определенной достоверностью, имеет свои преимущества и недостатки, Считается, что комбинированные методы прогнозирования (синтез прогнозов) позволяют компенсировать недостатки одних способов достоинствами других. На рис. 11.5 представлена блок-схема комбинированного прогноза для двух вариантов прогноза, один из которых – прогноз, выполненный эвристическим методом, основанным на статистической обработке мнений экспертов.
Рис. 11.5. Блок-схема выбора стратегии АТП
в целевом сегменте рынка транспортных услуг
Процедура получения экспертных оценок может быть формализована и представлена в виде блок-схемы (рис. 11.6).
Рис. 11.6. Блок-схема прогноза на основе экспертных опросов
Рассмотрим некоторые блоки подробнее.
Формирование группы экспертов – важнейшая составляющая экспертного метода. Не останавливаясь подробно на вопросах персонального подбора, затронем только количественную сторону, а именно число экспертов. Известно, что при прогнозировании в целях минимизации расходов на прогноз стремятся привлекать минимальное число экспертов при условии обеспечения ошибки результата прогнозирования не более Е, где 0 < Е < 1. Поэтому рекомендуемое число экспертов может быть определено по формуле:
(11.15)
При подстановке предельных значений Е находим: 
Таким образом, минимальное количество экспертов равно 4. Для определения максимальной численности экспертной группы используется неравенство:
(11.16)
где Ki – компетентность i-го эксперта, рассчитываемая на основе анкеты самооценки;
Kmax – максимально возможная компетентность по используемой шкале компетентности экспертов.
Статистический анализ результатов опроса предусматривает проведение двух взаимосвязанных процедур: традиционной статистической обработки в виде средних значений, дисперсий и т. п., а также оценки всей экспертной группы – степени согласованности, взаимосвязи и других показателей мнений экспертов. Оценка группы экспертов проводится с использованием части полученных статистических оценок. Если последние не удовлетворяют соответствующим критериям, то в блок-схеме предусмотрена корректировка, которая приводит, в частности, к изменению состава экспертов и повторной процедуре опроса.
Методика статистической обработки данных включает следующие этапы:
1. Определение для каждого фактора суммы рангов:
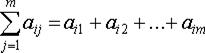(11.17)
где aij – ранг, присвоенный j-м экспертом i -му фактору;
m – число экспертов.
2. Определение средней величины суммы рангов:
(11.18)
где k – число факторов.
3. Определение суммы квадратов отклонений:
(11.19)
4. Определение коэффициента конкордации W, позволяющего оценить степень согласованности мнений экспертов (при отсутствии равных рангов):
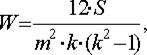(11.20)
Если W существенно отличается от нуля, то можно полагать, что между оценками экспертов существует определенное согласие.
5. Оценка неслучайности согласия мнений экспертов производится с помощью критерия Пирсена по величине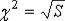 
.при числе степени свободы n = k – 1 и заданном уровне значимости α:
(11.21)
где 
– табличное значение.
В случае соблюдения неравенства с доверительной вероятностью 
можно утверждать, что мнения экспертов относительно вероятности факторов согласуются неслучайно.
Представленный вариант получения прогноза на основе экспертных оценок является универсальным и в случае использования баллов заканчивается построением ранжированной диаграммы рангов.
Для перехода к конкретному прогнозу, в частности объема перевозок, последовательности расчета сводятся к следующему:
1. Составляется ряд интервальных значений Qj возможных объемов перевозок для рассматриваемого клиента; разбивка на n интервалов осуществляется на основе F(Qj).
2. Эксперты оценивают значимость каждого Qj с использованием баллов, шкала которых охватывает n интервалов, т.е. j = 1, 2, …, n.
3. Проводится статистическая обработка оценок экспертов, и после ранжирования каждому Qj присваивается новый номер в порядке убывания, т.е. интервалу Qj с наименьшей суммой баллов присваивается номер 1 и т.д.
4. Полагаем, что интервалу Qj соответствует наиболее правдоподобная гипотеза (П1), затем вторая ((П2) и т.д.
Вероятности гипотез (П1), (П2), …., (Пn) определяются по формуле:
(11.22)
5. Восстанавливается функция распределения экспертного прогноза объема перевозок F(Qэj).
6. Для восстановленной «экспертной» функции находятся среднее значение и дисперсия Dэq.
Значения весовых коэффициентов для определения комбинированных оценок вероятностей каждого интервала находим по формулам:
(11.23)
где μ1 и Dq – весовой коэффициент и дисперсия экстраполяционного прогноза;
μ2 и Dэq – весовой коэффициент и дисперсия экспертного прогноза.
7. Вероятности F(Qj) для комбинированного прогноза рассчитываются следующим образом:
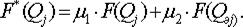(11.24)
Вопросы для повторения
Классификация методов прогнозирования.
Суть прогноза текущего расхода деталей на складе.
Расчет страхового запаса.
Метод комбинированного прогноза.
Маркетинговая информация как основа логистического планирования и прогнозирования
Задача планирования логистики - разработать проекты, устанавливающие на перспективу определенные параметры логистической деятельности, в результате чего достигается цель логистической системы предприятия.
Принятие решения - это выбор оптимальной альтернативы при заданной цели с учетом побочных условий.
Прогнозирование в логистике (прогноз) - вероятностное представление о появлении событий (последствий и данных) в будущем, основываемое на наблюдениях и теоретических положениях. Прогноз - прогностическая информация.
Планирование в логистике - систематическое принятие планово-управленческих решений в отношении физического перемещения и передачи собственности на продукцию от производителя к потребителю, включая транспортировку, хранение и совершение сделок.
План - это результат планирования.
Стратегическое планирование предприятия - деятельность по выработке плана с дальним прицелом, касающегося форм и способов поддержания существующего уровня бизнеса, его поддержания и развития в постоянно изменяющейся среде.
Этапы планирования:
• формулирование целей;
• постановка логистических проблем;
• поиск альтернатив;
• прогнозирование;
• оценка и принятие решений.
Система планирования - упорядоченная структура отдельных частей планирования.
По срокам различаются следующие виды планирования:
• стратегическое рамочное планирование;
• долгосрочное планирование;
• среднесрочное планирование;
• бюджетное планирование;
• скользящее краткосрочное планирование.
Планирование продаж определяет потребности в сырье, продукции и услугах, которые будут приобретены специалистами отдела закупок предприятия.
Планирование потребности в материалах - это система планирования, определяющая количество и график выпуска требуемой продукции, определяющая время и объем потребности в материалах в пределах периода планирования.
План потребности в материалах - разделенный на временные фазы график для планируемого выполнения заказов на закупку компонентов и материалов после принятия в расчет их наличного количества и ожидаемого цикла заказов, чтобы определить правильную дату размещения заказа на закупку.
Планирование производства:
• планирование количества изделий, необходимых для производства;
• планирование промежутка времени, в течение которого будет произведена продукция;
• планирование обеспечения сырья и оборудования для производства необходимого количества продукции в рамках запланированного периода времени.
Сглаживание данных
Анализ временных рядов - Две основные цели.
Имеются две основные цели анализа временных рядов:
а) определение природы ряда;
б) прогнозирование (предсказание будущих значений временного ряда по настоящим и прошлым значениям).
Обе эти цели требуют, чтобы модель ряда была идентифицирована и, более или менее, формально описана. Как только модель определена, Вы можете с ее помощью интерпретировать рассматриваемые данные (например, использовать в Вашей теории для понимания сезонного изменения цен на товары, если занимаетесь экономикой). Не обращая внимания на глубину понимания и справедливость теории, Вы можете экстраполировать затем ряд на основе найденной модели, т.е. предсказать его будущие значения.
Основные идеи и понятия
В дальнейшем нам понадобятся очень важные понятия, использующиеся в анализе временных рядов, такие как: тренд ряда, циклическая составляющая ряда, трендциклическая компонента ряда, сезонная составляющая ряда и шумовая компонента или просто шум. Дадим краткое пояснение данным элементам:
1. Формально Временной ряд - это ряд наблюдений анализируемой случайной величины 
, произведенных в последовательные моменты времени 
. В чем же состоят принципиальные отличия ряда от простой последовательности наблюдений, образующих случайную выборку? Этих отличий два:
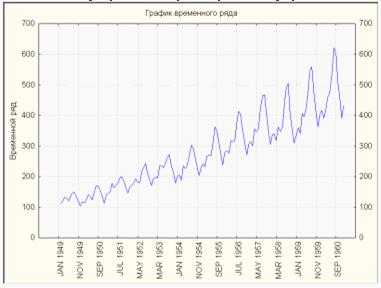
Рисунок 1. График временного ряда.
Во-первых, в отличие от элементов случайной выборки члены временного ряда не являются статистически независимыми.
Во-вторых, члены временного ряда не являются одинаково распределенными, т.е. верно следующее соотношение между вероятностями.
2. Трендом называют неслучайную функцию, формируемую под действием общих или долговременных тенденций, влияющих на наш ряд. Например, в качестве формирующей тенденции, может выступать фактор роста исследуемого рынка.
Не существует автоматического способа обнаружения тренда в временном ряде. Однако если тренд является монотонным (устойчиво возрастает или устойчиво убывает), то анализировать такой ряд обычно нетрудно. Если временные ряды содержат значительную ошибку, то первым шагом выделения тренда является сглаживание.
Сглаживание. Сглаживание всегда включает некоторый способ локального усреднения данных, при котором несистематические компоненты взаимно погашают друг друга. Самый общий метод сглаживания - скользящее среднее, в котором каждый член ряда заменяется простым или взвешенным средним n соседних членов, где n - ширина окна. Вместо среднего можно использовать медиану значений, попавших в окно. Основное преимущество медианного сглаживания, в сравнении со сглаживанием скользящим средним, в том, что результаты становятся более устойчивыми к выбросам (имеющимся внутри окна). Таким образом, если в данных имеются выбросы (связанные, например, с ошибками измерений), то сглаживание медианой обычно приводит к более гладким или, по крайней мере, более надежным кривым, по сравнению со скользящим средним с тем же самым окном. Основной недостаток медианного сглаживания в том, что при отсутствии явных выбросов, он приводит к более зубчатым кривым (чем сглаживание скользящим средним) и не позволяет использовать веса.
Все эти быстрые преобразования присутствуют в модуле Временные ряды. Относительно реже, когда ошибка измерения очень большая, используется сглаживание методом наименьших квадратов, взвешенных относительно расстояния или метод отрицательного экспоненциально взвешенного сглаживания. Все эти методы отфильтровывают шум и преобразуют данные в относительно гладкую кривую. Ряды с относительно небольшим количеством наблюдений и систематическим расположением точек могут быть сглажены с помощь бикубических сплайнов.
Подгонка функции. Многие монотонные временные ряды можно адекватно приблизить линейной функцией. Если же имеется явная монотонная нелинейная компонента, то данные вначале следует преобразовать, чтобы устранить нелинейность. Обычно для этого используют логарифмическое, экспоненциальное или (менее часто) полиномиальное преобразование данных. Имеется несколько способов выполнить эти преобразования в STATISTICA. Можно экспериментировать с преобразованиями практически неограниченной сложности, используя формулы таблиц исходных данных и далее анализировать преобразованные ряды с помощью линейной регрессии (в модуле Множественная регрессия или в модуле Временные ряды) и строить прогноз (Множественная регрессия). Нелинейные функции практически неограниченной сложности, включая кусочно-линейные с точками разрыва (различные функции могут быть одновременно подогнаны на различных участках ряда) могут быть получены в модуле Нелинейное оценивание. Наконец, STATISTICA предлагает подгонку различных кривых: полиномов (с определенным пользователем порядком), логарифмических функций (с определенным пользователем основанием), экспоненциальных и других.
3. Циклической компонентой также является неслучайная функция, обусловленная действием долговременных циклов различной природы.
4. Для удобства, вместо предыдущих двух понятий используют совместное понятие трендциклической компоненты (см. Классическая сезонная декомпозиция (Метод Census I)). Характер поведения отображен на рисунке.
Рисунок 2. График трендцицклической компоненты временного ряда.
5. Понятие сезон временного ряда или сезонная компонента используется для обозначения неслучайной функции. Данная функция формируется на основе периодически повторяющихся в определенное время года колебаний исследуемого ряда. Часто данную функцию измеряют в процентах, которые характеризуют сезонные отклонения от трендциклической компоненты. Пример данной функции приведен на рисунке.
Рисунок 3. График сезонной компоненты временного ряда.
Периодическая и сезонная зависимость (сезонность) представляет собой другой общий тип компонент временного ряда. Это понятие было проиллюстрировано ранее на примере авиаперевозок пассажиров. Можно легко видеть, что каждое наблюдение очень похоже на соседнее; дополнительно, имеется повторяющаяся сезонная составляющая, это означает, что каждое наблюдение также похоже на наблюдение, имевшееся в том же самом месяце год назад. В общем, периодическая зависимость может быть формально определена как корреляционная зависимость порядка k между каждым i-м элементом ряда и (ik)-м элементом. Ее можно измерить с помощью автокорреляции (т.е. корреляции между самими членами ряда); k обычно называют лагом (иногда используют эквивалентные термины: сдвиг, запаздывание). Если ошибка измерения не слишком большая, то сезонность можно определить визуально, рассматривая поведение членов ряда через каждые k временных единиц.
Автокорреляционная коррелограмма. Сезонные составляющие временного ряда могут быть найдены с помощью коррелограммы. Коррелограмма (автокоррелограмма) показывает численно и графически автокорреляционную функцию (AКФ), иными словами коэффициенты автокорреляции (и их стандартные ошибки) для последовательности лагов из определенного диапазона (например, от 1 до 30). На коррелограмме обычно отмечается диапазон в размере двух стандартных ошибок на каждом лаге, однако обычно величина автокорреляции более интересна, чем ее надежность, потому, что интерес в основном представляют очень сильные (а, следовательно, высоко значимые) автокорреляции.
Исследование коррелограмм. При изучении коррелограмм следует помнить, что автокорреляции последовательных лагов формально зависимы между собой. Рассмотрим следующий пример. Если первый член ряда тесно связан со вторым, а второй с третьим, то первый элемент должен также каким-то образом зависеть от третьего и т.д. Это приводит к тому, что периодическая зависимость может существенно измениться после удаления автокорреляций первого порядка, т.е. после взятия разности с лагом 1. Взятие разности также удаляет тренд, который обычно подавляет другие автокорреляции. Например, если имеется устойчивый линейный тренд, как в ряде авиаперевозок, то каждое наблюдение в большой степени является линейной функцией предыдущего наблюдения.
Частные автокорреляции. Другой полезный метод исследования периодичности состоит в исследовании частной автокорреляционной функции (ЧАКФ), представляющей собой углубление понятия обычной автокорреляционной функции. В ЧАКФ устраняется зависимость между промежуточными наблюдениями (наблюдениями внутри лага). Другими словами, частная автокорреляция на данном лаге аналогична обычной автокорреляции, за исключением того, что при вычислении из нее удаляется влияние автокорреляций с меньшими лагами. На лаге 1 (когда нет промежуточных элементов внутри лага), частная автокорреляция равна, очевидно, обычной автокорреляции. На самом деле, частная автокорреляция дает более чистую картину периодических зависимостей.
Удаление периодической зависимости. Как отмечалось выше, периодическая составляющая для данного лага k может быть удалена взятием разности соответствующего порядка. Это означает, что из каждого i-го элемента ряда вычитается (i-k)-й элемент. Имеются два довода в пользу таких преобразований.
Во-первых, таким образом можно определить скрытые периодические составляющие ряда. Напомним, что автокорреляции на последовательных лагах зависимы. Поэтому удаление некоторых автокорреляций изменит другие автокорреляции, которые, возможно, подавляли их, и сделает некоторые другие сезонные составляющие более заметными.
Во-вторых, удаление сезонных составляющих делает ряд стационарным, что необходимо для применения АРПСС и других методов, например, спектрального анализа.
6. Шумом во временном ряде, называют случайные не поддающиеся регистрации величины. Как и большинство других видов анализа, анализ временных рядов предполагает, что данные содержат систематическую составляющую (обычно включающую несколько компонент) и случайный шум (ошибку), который затрудняет обнаружение регулярных компонент. Большинство методов исследования временных рядов включает различные способы фильтрации шума, позволяющие увидеть регулярную составляющую более отчетливо.
Экстраполяция
Экстраполяция - метод научного прогнозирования, состоящий в распространении выводов, получаемых из наблюдения над одной частью явления на другую его часть.
Экстраполяция функции – продолжение функции за пределы её области определения, при котором продолженная функция (как правило, аналитическая) принадлежит заданному классу функций. Экстраполяция функций обычно происходит с помощью формул, в которых используется информация о поведении функции в некотором конечном наборе точек (в узлах экстраполяции), принадлежащих её области определения.
Понятие интерполирования функций иногда употребляется в качестве противопоставления понятию экстраполирования, когда конструктивно восстанавливаются (возможно, приближённо) значения функций в областях их определений.
Например, если используется информация о значениях функции, определённой на отрезке [a; b], в узлах хk из этого отрезка (k = 0; 1; …; n), то интерполяционный многочлен Лагранжа, поскольку он определён на всей числовой оси, является, в частности, экстраполяцией этой функции вне отрезка [a; b] в классе многочленов степени не выше n.
Название термина происходит от латинских слов extra – сверх, вне и polio – приглаживаю, направляю.
11. 5 Экспертные методы прогнозирования.
Основными преимуществами рассматриваемых методов являются возможность максимального использования индивидуальных способностей эксперта и незначительность психологического давления, оказываемого на отдельного работника. Однако эти методы мало пригодны для прогнозирования наиболее общих стратегий из-за ограниченности знаний одного специалиста-эксперта о развитии смежных областей науки.
Методы коллективных экспертных оценок основываются на принципах выявления коллективного мнения экспертов о перспективах развития объекта прогнозирования. В основе применения этих методов лежит гипотеза о наличии у экспертов умения с достаточной степенью достоверности оценить важность и значение исследуемой проблемы, перспективность развития определенного направления исследований, времени свершения того или иного события, целесообразности выбора одного из альтернативных путей развития объекта прогноза и т. д.
В настоящее время широкое распространение получили экспертные методы, основанные на работе специальных комиссий, когда группы экспертов за круглым столом обсуждают ту или иную проблему с целью согласования мнений и выработки единого мнения. Этот метод имеет недостаток, заключающийся в том, что группа экспертов в своих суждениях руководствуется в основном логикой компромисса.
В свою очередь в методе Дельфи вместо коллективного обсуждения той или иной проблемы проводится индивидуальный опрос экспертов обычно в форме анкет для выяснения относительной важности и сроков свершения гипотетических событий. Затем производится статистическая обработка анкет и формируется коллективное мнение группы, выявляются, обобщаются аргументы в пользу различных суждений. Вся информация сообщается экспертам. Участников экспертизы просят пересмотреть оценки и объяснить причины своего несогласия с коллективным суждением. Эта процедура повторяется 3–4 раза. В результате происходит сужение диапазона оценок.
Недостатком этого метода является невозможность учета влияния, оказываемого на экспертов организаторами опросов при составлении анкет.
Как правило, основными задачами при формировании прогноза с помощью коллектива экспертов являются: формирование репрезентативной экспертной группы, подготовка и проведение экспертизы, статистическая обработка полученных документов.
Из наиболее известных прогнозных экспертных методов стоит отметить следующие:
- Метод комиссий.
- Метод «лицом к лицу».
- Процедура дельфи.
- Морфологический анализ.
- «Мозговая атака».
- Метод фокальных объектов.
- Метод контрольных вопросов.
Метод экспертного прогнозирования. С помощью этого метода прогнозирования может быть решена большая часть проблем, возникающих при разработке прогнозов. В экспертном прогнозировании существует несколько основных этапов:
1.Подготовка к разработке прогноза;
2.Анализ ретроспективной информации, внутренних и внешних условий;
3.Определение наиболее вероятных вариантов развития внутренних и внешних условий;
4.Проведение экспертизы;
5.Разработка альтернативных вариантов;
6.Априорная и апостериорная оценка качества прогноза;
7.Контроль хода реализации прогноза и корректировка прогноза;
На стадии подготовки к разработке прогноза должны быть решены следующие задачи:
• подготовлено организационное обеспечение разработки прогноза,
• сформулировано задание на прогноз,
• сформулированы рабочая и аналитическая группы сопровождения,
• сформулирована экспертная комиссия,
• подготовлено методическое обеспечение разработки прогноза,
• подготовлена информационная база для проведения прогноза,
• подготовлено компьютерное сопровождение разработки прогноза.
После принятия решения о разработке прогноза необходимо назначить исполнителей для этой разработки. Этой группе работников поручается организационное обеспечение разработки прогноза. Они также должны обеспечить методическое и информационное его сопровождение.
Качественный экспертный прогноз может быть разработан только тогда, когда он хорошо подготовлен, если в его разработке задействованы компетентные специалисты, когда использована достоверная информация, когда оценки получены корректно и корректно обработаны.
Для разработки качественного прогноза необходимо использование современных технологий, сопровождающих и поддерживающих процесс разработки.
В состав экспертной комиссии приглашаются специалисты, профессионально знакомые с объектом экспертизы. Если требуется многоаспектная оценка объекта, либо оцениваться должны разнородные объекты и для этого нужны специалисты разных профессий, то экспертная комиссия должна быть сформирована таким образом, чтобы в её состав входили специалисты, способные профессионально оценить все основные аспекты прогнозируемой проблемы.
Задачей аналитической группы является методическая подготовка процесса прогнозирования. В состав аналитической группы входят специалисты, обладающие профессиональными знаниями и опытом проведения прогнозных разработок. Разработка прогноза должна быть проведена методически грамотно, применяемые методы должны соответствовать характеру прогнозируемой ситуации и характеру информации, которую предстоит получить, проанализировать и обработать. Также разработка прогноза должна быть четко регламентирована, то есть рабочая группа должна подготовить необходимую документацию, в состав которой входят: официально оформленное решение о проведении прогноза, состав экспертной комиссии, график разработки прогноза, контракты со специалистами, привлекаемыми для его разработки и т.д. Специалисты должны быть обеспечены всей необходимой информацией об объекте прогнозирования. Полезным может оказаться специально подготовленный аналитической группой аналитический обзор по прогнозируемой проблеме. При работе с многовариантными прогнозами приходится иметь дело с большими объемами информации, которая к тому же, должна анализироваться и обрабатываться в соответствии с используемой технологией разработки прогноза. Это невозможно сделать без компьютера и соответствующего программного обеспечения.
При анализе ретроспективой информации об объекте прогнозирования предполагается четкое разделение количественной и качественной информации. Количественная информация (достаточно надежная) используется для расчетов по экстраполяции динамики изменения прогнозируемых параметров, по определению наиболее вероятных тенденций их изменения. Качественная же информация классифицируется, систематизируется и служит основанием для оценок экспертов и используется для разработки экспертных прогнозов. При разработке прогноза необходим анализ внутренних условий объекта прогнозирования, содержательный анализ их особенностей и динамики развития.
Если разработаны математические, имитационные, аналоговые и другие модели функционирования объекта прогнозирования и изменения внутренних условий, то в них вводятся необходимые данные и на их основании производятся расчеты, позволяющие оценить наиболее вероятные изменения внутренних условий объекта прогнозирования.
При разработке прогноза, внешним условиям, внешней среде функционирования объекта прогнозирования должно уделяться не меньше внимания, чем внутренним.
Внутренняя среда, как внутреннее условие объекта прогнозирования, включает в себя: внутриорганизационные процессы, технологию, кадры, организационную культуру, управление функциональными процессами. Внешняя среда, включает общее внешнее окружение и непосредственно деловое окружение организации.
Определение наиболее вероятных вариантов развития внутренних и внешних условий объекта прогнозирования является одной из центральных задач разработки прогноза. На этом этапе разработки прогноза на основании анализа внутренних и внешних условий и всей имеющейся информации об объекте прогнозирования, информации в результате работы экспертной комиссии предварительно определяется перечень возможных альтернативных вариантов изменения внутренних и внешних условий. После их предварительной оценки, из перечня исключаются альтернативные варианты, реализуемость которых в прогнозируемые период сомнительна или же вероятность их реализации ниже предварительно установленного порогового значения. Оставшиеся альтернативные варианты подвергаются более углубленной оценке с целью определения альтернативных вариантов изменения внутренних и внешних условий, осуществление которых наиболее вероятно.
На этом этапе разработки прогноза предполагается наиболее активная работа экспертов по определению и оценке ключевых событий, наступление которых ожидается в прогнозируемом промежутке времени.
Предыдущий этап разработки прогноза дает информацию, необходимую аналитической группе для проведения экспертизы. Экспертам представляется информация о наиболее вероятном изменении внутренних и внешних условий, на основе ранее проведенного анализа формулируются вопросы, на которые должны быть получены ответы в результате проведения экспертизы, намечаются наиболее вероятные сценарии развития событий.
В зависимости от природы объекта прогнозирования, от характера оценок и суждений, которые должны быть получены в процессе проведения экспертизы, определяются конкретные способы организации и проведения экспертизы. Экспертизы могут быть одно-туровыми и много туровыми, анонимными и предусматривающие открытый обмен мнениями-т. д.
Разнообразные методы используются при сравнительной оценке объектов, при прогнозе количественных и качественных значений параметров прогнозируемого объекта, начиная от различных модификаций метода Делфи и кончая разнообразными процедурами метода мозговой атаки. Характер экспертной информации, которую предполагается использовать при разработке прогноза, накладывает определенные требования на выбор конкретного метода организации и проведения экспертизы. Если прогнозируемый объект достаточно сложен и многоаспектен, то целесообразно использование комплексных методов организации и проведения экспертизы при проведении экспертизы для разработки прогноза аналитическая группа может использовать анкетирование и интервьюирование.
Подготовленная на предыдущих этапах информация, в том числе и полученная от экспертов, используется при непосредственной разработке прогноза. Как правило, маловероятны случаи, когда заранее известно в каком направлении будут происходить изменения внутренних и внешних условий, какая стратегия будет выбрана организацией при том или ином развитии событий. Ведь развитие организации в прогнозируемом будущем зависит от различных факторов, а также от их сочетания и взаимодействия. Из этого можно сделать вывод, что при стратегическом планировании и в других случаях использования прогнозов необходимо рассматривать различные альтернативные варианты развития событий, как благоприятные, так и неблагоприятные.
На предыдущих этапах были определены наиболее вероятные изменения основных внутренних и внешних условий, определяющих ход прогнозируемых событий. Для наиболее вероятных альтернативных вариантов, их изменений, должны быть разработаны наиболее вероятные альтернативные варианты развития прогнозируемых событий.
Допустим, одной из целей разработки прогноза является определение динамики развития количественных показателей и параметров, то используется полученный на предыдущих этапах разработки прогноза объем информации (количественной и качественной) и соответствующие методы экстраполирования (определения изменения прогнозируемых показателей и параметров в будущем), рассчитываются кривые их изменения в прогнозируемом промежутке времени. Но мы не всегда имеем необходимую информацию для использования количественных методов экстраполяции. Эта черта характерна для современного этапа экономической жизни России, отсутствие необходимых для расчетов статистических данных, поскольку прежние экономические зависимости и закономерности изменились. Поэтому, как правило, единственным способом экстраполяции показателей и параметров на прогнозируемый промежуток времени остается способ построения экспертных кривых. Эти кривые отражают оценку динамики изменения прогнозируемых значений показателей и параметров экспертами.
Эксперты определяют критические точки, в которых тенденция изменения значений прогнозируемых показателей и параметров может измениться под действием тех или иных факторов. А затем, в каждой из критических точек, расположенных на оси времени, оцениваются ожидаемые значения прогнозируемых показателей и параметров, а также характер их изменения в интервале между двумя критическими точками.
При разработке вариантного прогноза должна быть произведена экстраполяция прогнозируемых значений показателей и параметров для различных вариантов исходных условий и для различных вариантов возможных альтернативных вариантов динамики их изменений. Вместе с этим, каждый альтернативный вариант разрабатываемого прогноза может сопровождаться описанием прогнозируемого развития событий.
Априорная и апостериорная оценка качества прогноза. Оценка качества прогноза – одна из центральных проблем в процессе разработки управленческих решений. Степень доверия к разработанному прогнозу во многом влияет на решение и сказывается на эффективности управленческих решений, принимаемых с использованием разработанного прогноза.
Однако оценка качества прогноза является достаточно сложной задачей не только в момент, когда прогноз только разработан (априорная оценка), но и в момент, когда прогнозируемое событие уже произошло (апостериорная оценка). Здесь следует также отметить тот факт, что качественный прогноз при принятии решения может быть использован по-разному.
Если со стороны руководства организации не оказывается значительное воздействие на ход развития событий, а лишь осуществляется наблюде
