Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие – это подмножество этой области, пространства элементарных исходов G. Можно считать, что все точки G «равноправны» и тогда вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.
Геометрическая вероятность события А определяется отношением:
,
где m(G), m(A) – геометрические меры (длины, площади или объемы) всего пространства элементарных исходов и события А.
Пример. На плоскость, разграфленную параллельными полосами шириной 2d, расстояние между осевыми линиями которых равно 2D, наудачу брошен круг радиуса r (
). Найти вероятность того, что круг пересечет некоторую полосу.
Решение. В качестве элементарного исхода этого испытания будем считать расстояние x от центра круга до осевой линии ближайшей к кругу полосы. Тогда все пространство элементарных исходов – это отрезок 
. Пересечение круга с полосой произойдет в том случае, если его центр попадет в полосу, т.е. 
, или будет находится от края полосы на расстоянии меньшем чем радиус, т.е. 
.
Для искомой вероятности получаем: 
.
3) Теоремы сложения и умножения вероятностей
События А и В называются несовместными, если они не могут произойти одновременно
События А и В называются совместными, если они могут произойти одновременно.
Суммой двух события А и В называется событие с, состоящее в выполнении события А или события В, или обоих вместе.
Сумой нескольких событий называется событие, состоящее в том, что появится хотя бы одно из этих событий.
Теорема сложения вероятностей несовместных событий
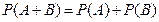
Теорема сложения вероятностей совместных событий
В случае четырех и более события данная формула еще больше усложняется
События А и В называются независимыми, если вероятность появления события А не зависит от появления события В и наоборот: вероятность события в не зависит от появления события А.
События А и В называются зависимыми, если вероятность события В зависит от того появилось ли событие А или наоборот.
Произведением двух события А и В называется событие С, состоящее в том, что события А и В появятся одновременно.
Произведением нескольких событий называется событие, состоящее вы том, что данные события появятся одновременно.
Теорема умножения вероятностей для независимых событий
