Основным понятием теории вероятностей является понятие случайного события. Случайным событием называется событие, которое при осуществлении некоторых условий может произойти или не произойти. Например, попадание в некоторый объект или промах при стрельбе по этому объекту из данного орудия является случайным событием.
Событие называется достоверным, если в результате испытания оно обязательно происходит. Невозможным называется событие, которое в результате испытания произойти не может.
Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.
Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.
Рассмотрим полную группу равновозможных несовместных случайных событий. Такие события будем называть исходами. Исход называется благоприятствующим появлению события А, если появление этого события влечет за собой появление события А.
Пример. В урне находится 8 пронумерованных шаров (на каждом шаре поставлено по одной цифре от 1 до 8). Шары с цифрами 1, 2, 3 красные, остальные – черные. Появление шара с цифрой 1 (или цифрой 2 или цифрой 3) есть событие, благоприятствующее появлению красного шара. Появление шара с цифрой 4 (или цифрой 5, 6, 7, 8) есть событие, благоприятствующее появлению черного шара.
Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу

Свойство 1. Вероятность достоверного события равна единице
Свойство 2. Вероятность невозможного события равна нулю.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.
Итак, вероятность любого события удовлетворяет двойному неравенству  .
.
Пример. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10?
Решение. Пусть событие А = (Номер вынутого шара не превосходит 10). Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m = n =10. Следовательно, Р (А)=1. Событие А достоверное.
Пример. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые?
Решение. Вынуть два шара из десяти можно следующим числом способов:  .
.
Число случаев, когда среди этих двух шаров будут два белых, равно  .
.
Искомая вероятность
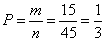 .
.






