Две прямые называются пересекающимися, если они имеют одну единственную общую точку. Эта общая точка двух прямых называется точкой пересечения прямых. Точка пересечения разбивает каждую из пересекающихся прямых на два луча. Очевидно, эти лучи образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Таким образом, если нам известна мера одного из углов, образованных двумя пересекающимися прямыми, то мы можем определить меры трех остальных углов. Действительно, пусть один из углов равен углу 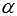 . Тогда вертикальный с ним угол также равен
. Тогда вертикальный с ним угол также равен 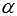 , а смежные с ним углы равны
, а смежные с ним углы равны  . Если
. Если  , то все четыре угла являются прямыми. В этом случае пересекающиеся прямые называются перпендикулярными (им посвящена статья перпендикулярные прямые).
, то все четыре угла являются прямыми. В этом случае пересекающиеся прямые называются перпендикулярными (им посвящена статья перпендикулярные прямые).
Условие параллельности и перпендикулярности прямых.
Условие параллельности
Если прямые линии параллельны, то они наклонены к числовой оси ОХ под одним и тем же углом, следовательно, разница углов наклона параллельных прямых равна нулю (действительно они никогда не пересекаются). Тангенс угла в ноль градусов (ноль радиан) равен нулю. То есть левая часть уравнения (1-4) равна нулю, тогда нулю должна быть равна и правая часть данного выражения. Дробь равна нулю если числитель равен нулю. В нашем случае это может быть при:
k2 = k1. (1-5)
Это и есть условие параллельности двух прямых линий.
Условие перпендикулярности
Если две прямых линии взаимно перпендикулярны, то угол между ними равен 90 или П /2 радиан. Тангенс такого угла не существует (иногда говорят, что он равен бесконечности). Правая часть (1-4) не существует при равенстве нулю знаменателя, т.е.
k2 * k1 = -1. (1-6)
Условие (1-6) или что тоже самое  является условием перпендикулярности заданных прямых.
является условием перпендикулярности заданных прямых.
Множества точек на плоскости.
Определение 1: окрестностью точки  (
( ) на плоскости называется круг, с центром в точке
) на плоскости называется круг, с центром в точке  некоторого радиуса
некоторого радиуса  , который не содержит окружности, ограничивающей данный круг.
, который не содержит окружности, ограничивающей данный круг.
Окрестность точки  радиуса r обозначаем
радиуса r обозначаем  (
( ,r).
,r).  (
( ,r) ={
,r) ={  +(
+(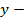
 }.
}.
Так как r– произвольное, то каждая точка М на плоскости имеет бесконечно много окрестностей.
Определение 2: Множество Е точек на плоскости называется открытым, если каждая точка множества Е принадлежит Е вместе с некоторой окрестностью.
26. Окружность и её уравнение.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Эллипс и его уравнение.
Каноническое уравнение эллипса имеет вид  , где
, где  – положительные действительные числа, причём
– положительные действительные числа, причём  .
.
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат.
28. Гипербола и её уравнение.
имеет вид 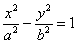 , где
, где  – положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие
– положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие  , то есть, значение «а» может быть и меньше значения «бэ».
, то есть, значение «а» может быть и меньше значения «бэ».
Гипербола может быть определена, как множество точек, образуемое в результате сечения кругового конусаплоскостью, отсекающей обе части конуса. Другими результатами сечения конуса плоскостью являются парабола,эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающиеся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
29. Парабола и её уравнение.

Пусть на плоскости заданы точка F и прямая  , не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой
, не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой  . Точка F называется фокусом, прямая
. Точка F называется фокусом, прямая  - директрисой параболы; (OF) - ось, O - вершина,
- директрисой параболы; (OF) - ось, O - вершина,  - параметр,
- параметр,  - фокус,
- фокус,  - фокальный радиус.
- фокальный радиус.
Каноническое уравнение: 
Эксцентриситет: 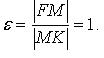
Фокальный радиус: 
Уравнение директрисы: 
Уравнение касательной в точке 

Свойство касательной к параболе:  (М - точка касания; N - точка пересечения касательной с осью Ox).
(М - точка касания; N - точка пересечения касательной с осью Ox).
Уравнение нормали в точке 

Уравнение диаметра, сопряженного хордам с угловым коэффициентом k: y = p/k.
Параметрические уравнения параболы: 
Полярное уравнение: 






