Запись комплексного числа z = a + bi в виде z = r  cos  + i sin  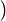называется тригонометрической формой комплексного числа.
Модуль комплексного числа: r =  a 2+ b 2
Аргумент комплексного числа:cos = ra  sin = rb
|
Свойство умножения: Произведение двух комплексных чисел z 1= r 1 
cos 
1+ i sin 1 
и z 2= r 2 cos 2+ i sin 2 будет комплексное число вида z 1 
z 2= r 1 r 2 cos ( 1+ 2)+ i sin( 1+ 2)
Свойство деления: Частное двух комплексных чисел z 1= r 1 cos 1+ i sin 1 и z 2= r 2 cos 2+ i sin 2 будет комплексное число вида z 2 z 1= r 2 r 1 cos ( 1− 2)+ i sin( 1− 2)
Свойство возведение в степень: Степень комплексного числа z = r cos + i sin будет комплексное число вида r cos + i sin n = rn cos n + i sin n
Свойство извлечения корня: Корень из комплексного числа z = r cos + i sin будет комплексное число вида 
nr cos + i sin = 
nr 
cos n 
+2 
k + i sin n +2 k 
k =0;1;2; 
; n −1
Формула Муавра: cos + i sin n =cos n + i sin n
Действия над комплексными числами, заданными в показательной форме.
Решение квадратных уравнений с отрицательными дискриминантами.
Понятие комплексного числа.
Рекомендация: не пытайтесь представить комплексное число в реальной жизни, это всё равно, что представить бесконечность, четвёртое измерение или что-то сверх нашего сознания.
Немного теории.
Комплексным числом z называется число вида
z = a + bi
где a и b – действительные числа, i – так называемая мнимая единица.
a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.
Мнимая единица равна корню из минус единицы:
Теперь рассмотрим уравнение:
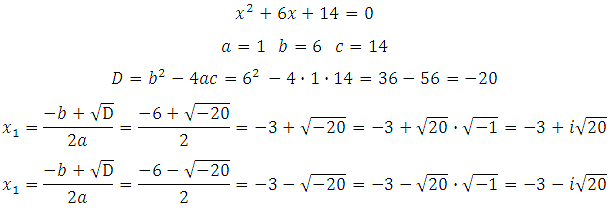
Векторы. Операции над векторами.
Координаты векторов. Действия над векторами, заданными своими координатами.
. При сложении двух (или большего числа) векторов их соответственные координаты складываются:
(x 1; y 1; z 1) + (x 2; y 2; z 2) = (x 1 + x 2; y 1 + y 2; z 1 + z 2).
В самом деле, для двух векторов (x 1; y 1; z 1) и (x 2; y 2; z 2) имеем
(x 1; y 1; z 1) + (x 2; y 2; z 2) =
= (x 1 e 1 + y 1 e 2 + z 1 e 3) + (x 2 e 1 + y 2 e 2 + z 2 e 3) =
= (x 1 + x 2) e 1 + (y 1 + y 2) e 2 + (z 1 + z 2) e 3 =
= (x 1 + x 2; y 1 + y 2; z 1 + z 2).
Для суммы трех или большего числа векторов доказательство проводится аналогично.
2. При вычитании векторов их соответственные координаты вычитаются:
(x 1; y 1; z 1) — (x 2; y 2; z 2) = (x 1 — x 2; y 1 — y 2; z 1 — z 2)
Доказательство проведите самостоятельно.
3. При умножении вектора на число все его координаты умножаются на это число.
В самом деле, для вектора (x 1; y 1; z 1) и числа λ, имеем
λ (x 1; y 1; z 1) = λ (x 1 e 1 + y 1 e 2 + z 1 e 3) =
= (λ x 1) e 1+ (λ y 1) e 2 + (λ z 1) e 3 = (λ x 1; λ y 1; λ z 1)
Деление отрезка в данном отношении.
Если точка М(x; y) лежит на прямой, проходящей через две данные точк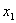и 
(
, 
) и 
(
, 
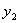), и дано отношение 
, в котором точка М делит отрезок 
, то координаты точки М определяются по формулам
, 
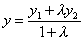.Если точка М является серединой отрезка , то ее координаты определяются по формулам 
, 
.
Длина вектора.
Формула длины вектора для плоских задач
В случае плоской задачи модуль вектора a = {ax; ay} можно найти воспользовавшись следующей формулой:
|a| = √ax2 + ay2
