Необхідна умова збіжності
Якщо ряд збігається, то його загальний член 
прямує до нуля при 
, тобто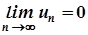 
.
Наслідок. Якщо 
, то ряд розбігається.
Ознака збіжності Даламбера
Якщ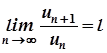о 
, то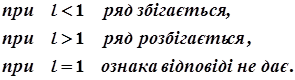 
Гранична ознака порівняння
Нехай є два ряди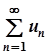 
, 
.
Якщо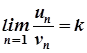 
, де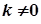 
, 
, то ці два ряди або одночасно збігаються, або одночасно розбігаються.
Такі ряди називають еквівалентними та позначають це так:
.
Знакопочережні ряди
Числовий ряд називається знакопочережним, якщо його члени, що стоять поруч, мають різні знаки.
Такі ряди мають вигляд:
, (1)
, (2)
де 
абсолютна величина члена ряду.
Ознака Лейбніця
Якщо в знакопочережному ряді (2) члени такі, що
1) 
2) 
,
то ряд збігається, а його сума за абсолютним значенням не перевершує перший член ряду.
Знакопочережний ряд називається умовно збіжним, якщо він збігається, а ряд, складений з абсолютних величин його членів, розбігається.
Знакопочережний ряд називається абсолютно збіжним, якщо збігається ряд з абсолютних величин його членів.
Елементи комбінаторики. Початки теорії ймовірностей
Перестановками із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення. Кількість таких упорядкованих множин обчислюється за формулою: 
Розміщенням із n елементів по m
(0 
m n) називаються такі впорядковані множини, кожна із яких містить m елементів і які відрізняються між собою порядком розташування цих елементів або хоча б одним елементом: 
.
Комбінаціями(сполученнями) з n елементів по m
(0 m n) називаються такі множини з m елементів, які різняться між собою хоча б одним елементом: 
.
Випробування — реальний або мислений експеримент (виконуваний за певної незмінної сукупності умов), результати якого піддаються спостереженню.
Подія — результат випробування. Якщо в результаті випробування деяка подія неодмінно відбудеться, то вона називається достовірною. Подія, яка в даному випробуванні не може відбутись, називається неможливою. Якщо в результаті випробування деяка подія може відбутись, а може не відбутись, то вона називається випадковою. Випадкові події позначаються літерами A, B, C, D, …
Класичною ймовірністю випадкової події А називається відношення кількості елементарних подій m, які сприяють появі цієї події (становлять множину її елементарних подій), до загальної кількості n рівноможливих елементарних подій, що утворюють простір елементарних подій W:
P(A)= m /n.
КОНТРОЛЬНА РОБОТА №2
Тема: Визначений та невласний інтеграли.
